人教版八年级上数学教学讲义,复习补习资料(含知识讲解,巩固练习):25【基础】等边三角形含答案
文档属性
| 名称 | 人教版八年级上数学教学讲义,复习补习资料(含知识讲解,巩固练习):25【基础】等边三角形含答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 227.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-03 00:00:00 | ||
图片预览



文档简介
等边三角形(基础)
【学习目标】
1. 掌握等边三角形的性质和判定.
2. 掌握含30°角的直角三角形的一个主要性质.
3. 熟练运用等边三角形的判定定理与性质定理进行推理和计算.
【要点梳理】
【 等边三角形,知识要点】
要点一、等边三角形 等边三角形定义:
三边都相等的三角形叫等边三角形.
要点诠释:由定义可知,等边三角形是一种特殊的等腰三角形.也就是说等腰三角形包
括等边三角形.
要点二、等边三角形的性质
等边三角形的性质:
等边三角形三个内角都相等,并且每一个内角都等于60°.
要点三、等边三角形的判定 等边三角形的判定:
(1)三条边都相等的三角形是等边三角形;
(2)三个角都相等的三角形是等边三角形;
(3)有一个角是60°的等腰三角形是等边三角形.
要点四、含30°的直角三角形 含30°的直角三角形的性质定理:
在直角三角形中,如果有一个锐角是30°,那么它所对的直角边等于斜边的一半.
要点诠释:这个定理的前提条件是“在直角三角形中”,是证明直角三角形中一边等于另一边(斜边)的一半的重要方法之一,通常用于证明边的倍数关系.
【典型例题】
类型一、等边三角形
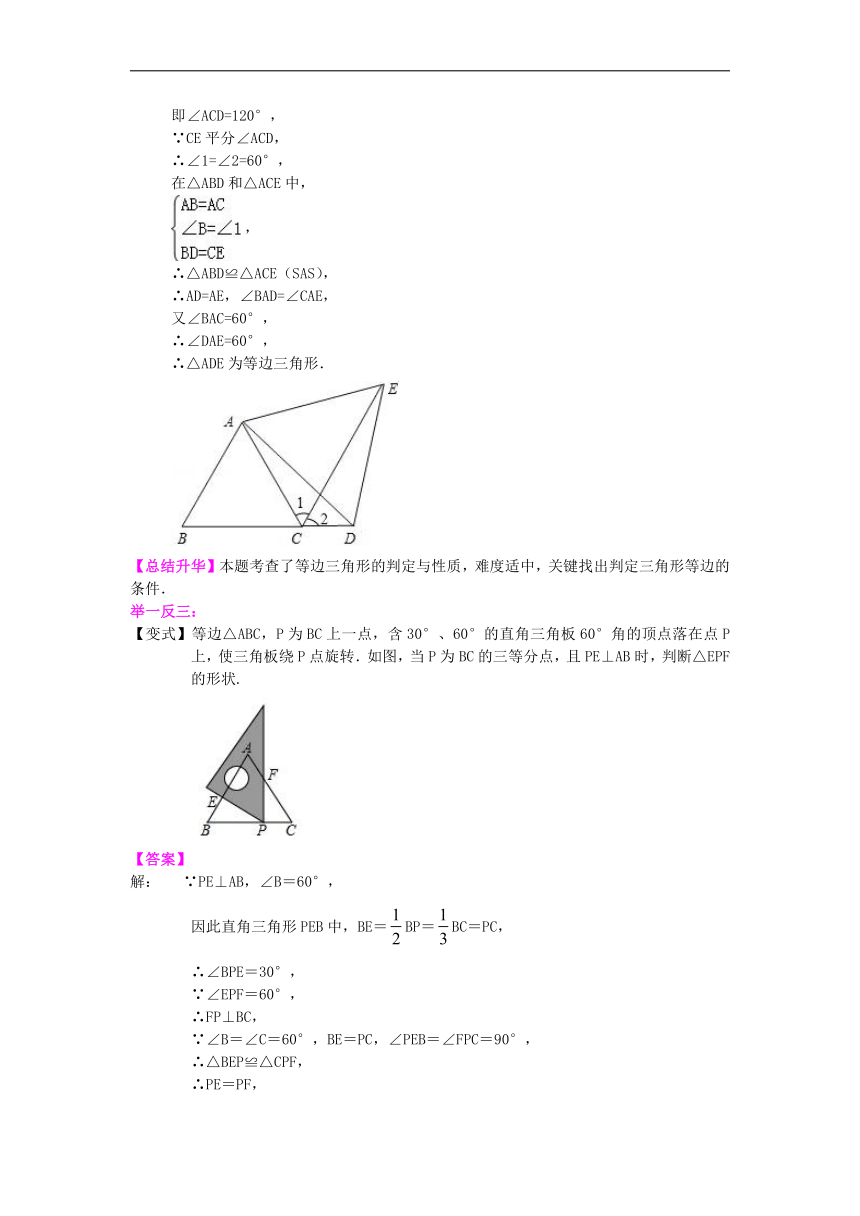
1、(2019秋?崇州市期末)如图,已知△ABC为等边三角形,D为BC延长线上的一点,CE平分∠ACD,CE=BD,求证:△ADE为等边三角形.
【思路点拨】由条件可以容易证明△ABD≌△ACE,进一步得出AD=AE,∠BAD=∠CAE,加上∠DAE=60°,即可证明△ADE为等边三角形.
【答案与解析】
证明:∵△ABC为等边三角形,
∴∠B=∠ACB=60°,AB=AC,
即∠ACD=120°,
∵CE平分∠ACD,
∴∠1=∠2=60°,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴AD=AE,∠BAD=∠CAE,
又∠BAC=60°,
∴∠DAE=60°,
∴△ADE为等边三角形.
【总结升华】本题考查了等边三角形的判定与性质,难度适中,关键找出判定三角形等边的条件.
举一反三:
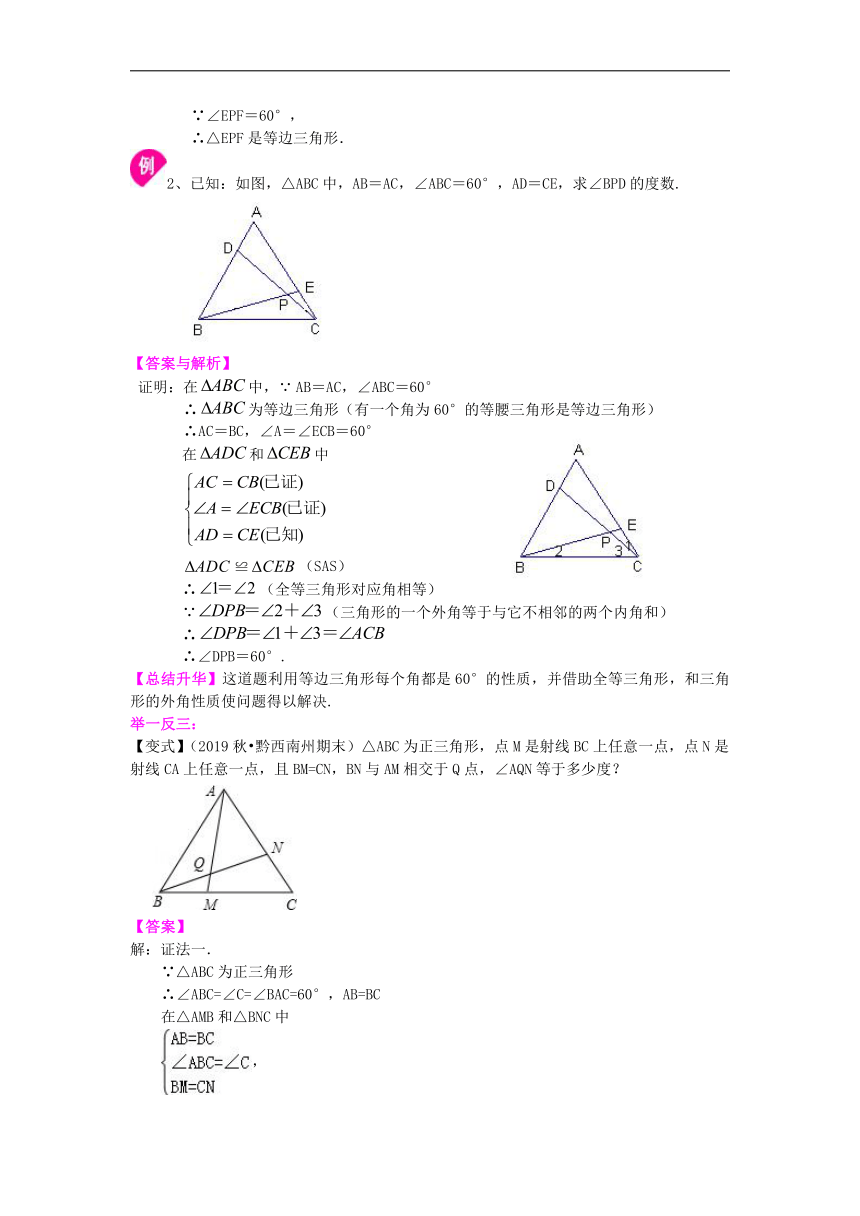
【变式】等边△ABC,P为BC上一点,含30°、60°的直角三角板60°角的顶点落在点P上,使三角板绕P点旋转.如图,当P为BC的三等分点,且PE⊥AB时,判断△EPF的形状.
【答案】
解: ∵PE⊥AB,∠B=60°,
因此直角三角形PEB中,BE=BP=BC=PC,
∴∠BPE=30°,
∵∠EPF=60°,
∴FP⊥BC,
∵∠B=∠C=60°,BE=PC,∠PEB=∠FPC=90°,
∴△BEP≌△CPF,
∴PE=PF,
∵∠EPF=60°,
∴△EPF是等边三角形.
2、已知:如图,△ABC中,AB=AC,∠ABC=60°,AD=CE,求∠BPD的度数.
【答案与解析】
证明:在中,AB=AC,∠ABC=60°
∴为等边三角形(有一个角为60°的等腰三角形是等边三角形)
∴AC=BC,∠A=∠ECB=60°
在和中
≌(SAS)
∴(全等三角形对应角相等)
(三角形的一个外角等于与它不相邻的两个内角和)
∴
∴∠DPB=60°.
【总结升华】这道题利用等边三角形每个角都是60°的性质,并借助全等三角形,和三角形的外角性质使问题得以解决.
举一反三:
【变式】(2019秋?黔西南州期末)△ABC为正三角形,点M是射线BC上任意一点,点N是射线CA上任意一点,且BM=CN,BN与AM相交于Q点,∠AQN等于多少度?
【答案】
解:证法一.
∵△ABC为正三角形
∴∠ABC=∠C=∠BAC=60°,AB=BC
在△AMB和△BNC中
,
△AMB≌△BNC(SAS),
∵∠ANB=∠C+∠NBC=60°+∠NBC,
∠MAN=∠BAC﹣∠MAB=60°﹣∠MAB,
又∵∠NBC=∠MAB(全等三角形对应角相等),
∴∠ANB+∠MAN=120°,
又∵∠ANQ+∠MAN+∠AQN=180°,
∴∠AQN=180°﹣∠ANB﹣∠MAN,
∠AQN=180°﹣(∠ANB+∠MAN),
=180°﹣120°=60°,
∠BOM=∠AQN=60°(全等三角形对应角相等).
证法二.
∵△ABC为正三角形
∴∠ABC=∠C=∠BAC=60°,AB=BC
在△AMB和△BNC中
∴△AMB≌△BNC(SAS)
∵∠ANB=∠C+∠NBC=60°+∠NBC
∠MAN=∠BAC﹣∠MAB
又∵∠NBC=∠MAB(全等三角形对应角相等)
∴∠ANB+∠MAN=120°
又∵∠ANQ+∠MAN+∠AQN=180°
∴∠AQN=180°﹣∠ANB﹣∠MAB
∠AQN=180°﹣(∠ANB+∠MAN)
=180°﹣120°=60°
3、(1)如图,点O是线段AD的中点,分别以AO和DO为边在线段AD的同侧作等边三角形OAB和等边三角形OCD,连接AC和BD,相交于点E,连接BC,求∠AEB的大小;
(2)如图,△OAB固定不动,保持△OCD的形状和大小不变,将△OCD绕着点O旋转(△OAB和△OCD不能重叠),求∠AEB的大小.
【思路点拨】(1)由于△OCD和△OAB都是等边三角形,可得OD=OC=OB=OA,进而求出∠BDA与∠CAD的大小及关系,则可求解∠AEB.(2)旋转后,△BOD与△AOC仍然保持全等,∠ACO=∠BDO,∠AED=∠ACO+∠DCO+∠CDB=∠BDO+60°+∠CDB=60°+∠CDO=120°,从而得到∠AEB的值.
【答案与解析】
证明:(1)∵O是AD的中点,
∴AO=DO
又∵等边△AOB和等边△COD
∴AO=DO=CO=BO,∠DOC=∠BOC=∠AOB=60°
∴∠CAO=∠ACO=∠BDO=∠DBO=30°
∴∠AEB=∠BDO +∠CAO =60°
(2)∵∠BOD=∠DOC+∠BOC,∠AOC=∠AOB+∠BOC
∴∠BOD=∠AOC
在△BOD与△AOC中,
∴△BOD≌△AOC(SAS)
∴∠ACO=∠BDO
∵∠AED=∠ACO+∠DCO+∠CDB
=∠BDO+60°+∠CDB=60°+∠CDO=60°+60°=120°
∴∠AEB=180°-∠AED=60°.
【总结升华】这道题利用等边三角形每个角都是60°的性质,并借助全等三角形,和三角形的外角性质使问题加以解决.
举一反三:
【变式】如图,已知△ABC和△CDE都是等边三角形,AD、BE交于点F,求∠AFB 的度数.
【答案】
解:∵△ABC和△CDE都是等边三角形,
∴AC=BC,CE=CD,
又∵∠ACB+∠BCD=∠ECD+∠BCD,即∠ACD=∠BCE,
∴△ACD≌△BCE,
∴∠CAD=∠CBE,
设AD与BC相交于P点,在△ACP和△BFP中,有一对对顶角,
∴∠AFB=∠ACB=60°.
类型二、含30°的直角三角形
4、(2019春·龙口市期末)如图,E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD交OE于点F,若∠AOB=60°.
(1)求证:△OCD是等边三角形;
(2)若EF=5,求线段OE的长.
【答案与解析】
解:(1)∵点E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,
∴DE=CE,
在Rt△ODE和Rt△OCE中,
∴Rt△ODE≌Rt△OCE(LH)
∴OD=OC,
∵∠AOB=60°,
∴△OCD是等边三角形;
(2)∵△OCD是等边三角形,OF是角平分线,
∴OE⊥DC,
∵∠AOB=60°,
∴∠AOE=∠BOE=30°,
∵∠ODF=60°,ED⊥OA,
∴∠EDF=30°,
∴DE=2EF=10,
∴OE=2DE=20.
【总结升华】本题考查等边三角形的判定和性质,角平分线的性质,三角形全等的判定和性质,30°的直角三角形的性质等,熟练掌握性质和定理是解题的关键。
举一反三:
【 等边三角形:例5】
【变式】如图, △ABC中, ∠ACB=90°, ∠ABC=60°, AB的中垂线交BC的延长线于D,交AC于E, 已知DE=2.则 AC的长为_________.
【答案】3;
提示:连接AD,证△ABD为等边三角形,则DE=AE=2,CE=1,所以AC=3.
【巩固练习】
一.选择题
1. (2019?陕西一模)已知:如图,在△ABC中,D为BC的中点,AD⊥BC,E为AD上一点,∠ABC=60°,∠ECD=40°,则∠ABE=( )
A.10° B.15° C.20° D.25°
2.以下叙述中不正确的是( ).
A.等边三角形的每条高线都是角平分线和中线;
B.有一个内角为60°的等腰三角形是等边三角形;
C.等腰三角形一定是锐角三角形;
D.在一个三角形中,如果有两条边相等,那么它们所对的角也相等;反之,在一个三角形中,如果有两个角相等,那么它们所对的边也相等.
3.(2019秋?荔湾区期末)如图,若△ABC是等边三角形,AB=6,BD是∠ABC的平分线,延长BC到E,使CE=CD,则BE=( )
A.7 B. 8 C. 9 D. 10
4. △ABC中三边为、、,满足关系式 (-)(-)(-)=0,则这个三角形一定为 ( )
A.等边三角形 B.等腰三角形
C.等腰钝角三角形 D.等腰直角三角形
5. 等边三角形的两条高线相交成钝角的度数是( )
A.105° B.120° C.135° D.150°
6. 如图,等边三角形ABC中,D为BC的中点,BE平分∠ABC交AD 于E,若△CDE的面积等于1,则△ABC的面积等于( )
A.2 B.4 C.6 D.12
二.填空题
7. (2019?黔南州)如图,在△ABC中,∠C=90°,∠B=30°,AB的垂直平分线ED交AB于点E,交BC于点D,若CD=3,则BD的长为 .
8.如图,△ABC为等边三角形,DC∥AB,AD⊥CD于D.若△ABC的周长为12,则CD =________.
9. 下列命题是真命题的是_________.
①有一个外角是120°的等腰三角形是等边三角形.
②有两个外角相等的等腰三角形是等边三角形.
③有一边上的高也是这边上的中线的等腰三角形是等边三角形.
④三个外角都相等的三角形是等边三角形.
10.△ABC为等边三角形,D、E、F分别在边BC、CA、AB上,且AE=CD=BF,则△DEF为_____三角形.
11.如图所示,△ABC为等边三角形,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,则四个结论正确的是 .
①P在∠A的平分线上; ②AS=AR;③QP∥AR;④△BRP≌△QSP.
12.如图,是等边三角形,点是边上任意一点,于点, 于点.若,则_____________.
三.解答题
13. 已知:如图,△ABD为等边三角形,△ACB为等腰三角形且∠ACB=90°,DE⊥AC交AC延长线于E,求证:DE=CE.
14.(2019秋?大英县校级期末)已知:等边△ABC和点P,设点P到△ABC的三边AB、AC、BC的距离分别为h1、h2、h3,△ABC的高为h.
(1)如图1,若点P在边BC上,证明:h1+h2=h.
(2)如图2,当点P在△ABC内时,猜想h1、h2、h3和h有什么关系?并证明你的结论.
(3)如图3,当点P在△ABC外时,h1、h2、h3和h有什么关系?(不需要证明)
15. 如图,直角△ACB中,∠ABC=90°,∠BAC=30°,而△ACD和△ABE都是等边三角形,AC,DE交于F.求证:FD=FE且CF=3AF.
【答案与解析】
选择题
1. 【答案】C;
【解析】∵D为BC的中点,AD⊥BC,∴EB=EC,AB=AC;
∴∠EBD=∠ECD,∠ABC=∠ACD.
又∵∠ABC=60°,∠ECD=40°,
∴∠ABE=60°﹣400=200.
2. 【答案】C;
【解析】等腰三角形顶角还可能是直角或钝角.
3. 【答案】C;
【解析】证明:∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,
∵BD是∠ABC的平分线,
∴AD=CD=AC,∠DBC=∠ABC=30°,
∵CE=CD,
∴CE=AC=3
∴BE=BC+CE=6+3=9.
故选C.
4. 【答案】B;
【解析】由题意=或=或=,这个三角形一定是等腰三角形.
5. 【答案】B;
【解析】等边△ABC的两条高线相交于O,∠OAB=∠OBA=30°,故∠AOB=120°.
6. 【答案】C;
【解析】AE=2DE,△ABC的面积是△CDE面积的6倍.
二.填空题
7. 【答案】6;
【解析】 ∵DE是AB的垂直平分线,
∴AD=BD,
∴∠DAE=∠B=30°,
∴∠ADC=60°,
∴∠CAD=30°,
∴AD为∠BAC的角平分线,
∵∠C=90°,DE⊥AB,
∴DE=CD=3,
∵∠B=30°,
∴BD=2DE=6.
8. 【答案】2;
【解析】在直角三角形中,30°的直角边等于斜边的一半.
9. 【答案】①④
【解析】②一般等腰三角形的两个底角的外角都相等;③等腰三角形底边上的高就是底边的中线.
10.【答案】等边;
【解析】利用SAS可以判定△EAF≌△FBD≌△DCE,从而可得,EF=FD=DE,即△DEF为等边三角形.
11.【答案】①②③④;
12.【答案】2;
【解析】BE=BD;CF=DC,(BD+DC)=2.
三.解答题
13.【解析】
证明:连接DC,
∵△ABD为等边三角形,
∴∠DAB=∠DBA=60°
又∵△ACB为等腰三角形且∠ACB=90°,
∴∠CAB=∠CBA=45°,∠BDC=∠ADC=30°
∴∠CBD=15°,∠DCB=180°-30°-15°=135°
又∵AC⊥BC,∴∠DCE=45°
∵DE⊥AC
∴ΔDEC为等腰直角三角形
∴DE=CE
14.【解析】
解:(1)如图1,连接AP,则 S△ABC=S△ABP+S△APC
∴BC?AM=AB?PD+AC?PF
即 BC?h=AB?h1+AC?h2
又∵△ABC是等边三角形
∴BC=AB=AC,
∴h=h1+h2.
(2)h=h1+h2+h3 ,理由如下:
如图2,连接AP、BP、CP,则 S△ABC=S△ABP+S△BPC+S△ACP
∴BC?AM=AB?PD+AC?PF+BC?PE
即BC?h=AB?h1+AC?h2+BC?h3
又∵△ABC是等边三角形,
∴BC=AB=AC.
∴h=h1+h2+h3.
(3)h=h1+h2﹣h3.
理由如下:如图3,连接PB,PC,PA
由三角形的面积公式得:S△ABC=S△PAB+S△PAC﹣S△PBC,
即BC?AM=AB?PD+AC?PE﹣BC?PF,
∵AB=BC=AC,
∴h1+h2﹣h3=h,
即h1+h2﹣h3=h.
15.【解析】
证明:作DG⊥AC于G,
∵△ACD和△ABE都是等边三角形,
∴∠CDG=30°,DC=AC,AB=AE,CG=AG
在△ABC与△DGC中
∴△ABC≌△DGC(AAS)
∴DG=AB=AE
在△DGF和△EAF中,
∴△DGF≌△EAF(AAS)
∴AF=GF,FD=FE
∵CG=AG,AF+GF=AG
∴CF=3AF.
【学习目标】
1. 掌握等边三角形的性质和判定.
2. 掌握含30°角的直角三角形的一个主要性质.
3. 熟练运用等边三角形的判定定理与性质定理进行推理和计算.
【要点梳理】
【 等边三角形,知识要点】
要点一、等边三角形 等边三角形定义:
三边都相等的三角形叫等边三角形.
要点诠释:由定义可知,等边三角形是一种特殊的等腰三角形.也就是说等腰三角形包
括等边三角形.
要点二、等边三角形的性质
等边三角形的性质:
等边三角形三个内角都相等,并且每一个内角都等于60°.
要点三、等边三角形的判定 等边三角形的判定:
(1)三条边都相等的三角形是等边三角形;
(2)三个角都相等的三角形是等边三角形;
(3)有一个角是60°的等腰三角形是等边三角形.
要点四、含30°的直角三角形 含30°的直角三角形的性质定理:
在直角三角形中,如果有一个锐角是30°,那么它所对的直角边等于斜边的一半.
要点诠释:这个定理的前提条件是“在直角三角形中”,是证明直角三角形中一边等于另一边(斜边)的一半的重要方法之一,通常用于证明边的倍数关系.
【典型例题】
类型一、等边三角形
1、(2019秋?崇州市期末)如图,已知△ABC为等边三角形,D为BC延长线上的一点,CE平分∠ACD,CE=BD,求证:△ADE为等边三角形.
【思路点拨】由条件可以容易证明△ABD≌△ACE,进一步得出AD=AE,∠BAD=∠CAE,加上∠DAE=60°,即可证明△ADE为等边三角形.
【答案与解析】
证明:∵△ABC为等边三角形,
∴∠B=∠ACB=60°,AB=AC,
即∠ACD=120°,
∵CE平分∠ACD,
∴∠1=∠2=60°,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴AD=AE,∠BAD=∠CAE,
又∠BAC=60°,
∴∠DAE=60°,
∴△ADE为等边三角形.
【总结升华】本题考查了等边三角形的判定与性质,难度适中,关键找出判定三角形等边的条件.
举一反三:
【变式】等边△ABC,P为BC上一点,含30°、60°的直角三角板60°角的顶点落在点P上,使三角板绕P点旋转.如图,当P为BC的三等分点,且PE⊥AB时,判断△EPF的形状.
【答案】
解: ∵PE⊥AB,∠B=60°,
因此直角三角形PEB中,BE=BP=BC=PC,
∴∠BPE=30°,
∵∠EPF=60°,
∴FP⊥BC,
∵∠B=∠C=60°,BE=PC,∠PEB=∠FPC=90°,
∴△BEP≌△CPF,
∴PE=PF,
∵∠EPF=60°,
∴△EPF是等边三角形.
2、已知:如图,△ABC中,AB=AC,∠ABC=60°,AD=CE,求∠BPD的度数.
【答案与解析】
证明:在中,AB=AC,∠ABC=60°
∴为等边三角形(有一个角为60°的等腰三角形是等边三角形)
∴AC=BC,∠A=∠ECB=60°
在和中
≌(SAS)
∴(全等三角形对应角相等)
(三角形的一个外角等于与它不相邻的两个内角和)
∴
∴∠DPB=60°.
【总结升华】这道题利用等边三角形每个角都是60°的性质,并借助全等三角形,和三角形的外角性质使问题得以解决.
举一反三:
【变式】(2019秋?黔西南州期末)△ABC为正三角形,点M是射线BC上任意一点,点N是射线CA上任意一点,且BM=CN,BN与AM相交于Q点,∠AQN等于多少度?
【答案】
解:证法一.
∵△ABC为正三角形
∴∠ABC=∠C=∠BAC=60°,AB=BC
在△AMB和△BNC中
,
△AMB≌△BNC(SAS),
∵∠ANB=∠C+∠NBC=60°+∠NBC,
∠MAN=∠BAC﹣∠MAB=60°﹣∠MAB,
又∵∠NBC=∠MAB(全等三角形对应角相等),
∴∠ANB+∠MAN=120°,
又∵∠ANQ+∠MAN+∠AQN=180°,
∴∠AQN=180°﹣∠ANB﹣∠MAN,
∠AQN=180°﹣(∠ANB+∠MAN),
=180°﹣120°=60°,
∠BOM=∠AQN=60°(全等三角形对应角相等).
证法二.
∵△ABC为正三角形
∴∠ABC=∠C=∠BAC=60°,AB=BC
在△AMB和△BNC中
∴△AMB≌△BNC(SAS)
∵∠ANB=∠C+∠NBC=60°+∠NBC
∠MAN=∠BAC﹣∠MAB
又∵∠NBC=∠MAB(全等三角形对应角相等)
∴∠ANB+∠MAN=120°
又∵∠ANQ+∠MAN+∠AQN=180°
∴∠AQN=180°﹣∠ANB﹣∠MAB
∠AQN=180°﹣(∠ANB+∠MAN)
=180°﹣120°=60°
3、(1)如图,点O是线段AD的中点,分别以AO和DO为边在线段AD的同侧作等边三角形OAB和等边三角形OCD,连接AC和BD,相交于点E,连接BC,求∠AEB的大小;
(2)如图,△OAB固定不动,保持△OCD的形状和大小不变,将△OCD绕着点O旋转(△OAB和△OCD不能重叠),求∠AEB的大小.
【思路点拨】(1)由于△OCD和△OAB都是等边三角形,可得OD=OC=OB=OA,进而求出∠BDA与∠CAD的大小及关系,则可求解∠AEB.(2)旋转后,△BOD与△AOC仍然保持全等,∠ACO=∠BDO,∠AED=∠ACO+∠DCO+∠CDB=∠BDO+60°+∠CDB=60°+∠CDO=120°,从而得到∠AEB的值.
【答案与解析】
证明:(1)∵O是AD的中点,
∴AO=DO
又∵等边△AOB和等边△COD
∴AO=DO=CO=BO,∠DOC=∠BOC=∠AOB=60°
∴∠CAO=∠ACO=∠BDO=∠DBO=30°
∴∠AEB=∠BDO +∠CAO =60°
(2)∵∠BOD=∠DOC+∠BOC,∠AOC=∠AOB+∠BOC
∴∠BOD=∠AOC
在△BOD与△AOC中,
∴△BOD≌△AOC(SAS)
∴∠ACO=∠BDO
∵∠AED=∠ACO+∠DCO+∠CDB
=∠BDO+60°+∠CDB=60°+∠CDO=60°+60°=120°
∴∠AEB=180°-∠AED=60°.
【总结升华】这道题利用等边三角形每个角都是60°的性质,并借助全等三角形,和三角形的外角性质使问题加以解决.
举一反三:
【变式】如图,已知△ABC和△CDE都是等边三角形,AD、BE交于点F,求∠AFB 的度数.
【答案】
解:∵△ABC和△CDE都是等边三角形,
∴AC=BC,CE=CD,
又∵∠ACB+∠BCD=∠ECD+∠BCD,即∠ACD=∠BCE,
∴△ACD≌△BCE,
∴∠CAD=∠CBE,
设AD与BC相交于P点,在△ACP和△BFP中,有一对对顶角,
∴∠AFB=∠ACB=60°.
类型二、含30°的直角三角形
4、(2019春·龙口市期末)如图,E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD交OE于点F,若∠AOB=60°.
(1)求证:△OCD是等边三角形;
(2)若EF=5,求线段OE的长.
【答案与解析】
解:(1)∵点E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,
∴DE=CE,
在Rt△ODE和Rt△OCE中,
∴Rt△ODE≌Rt△OCE(LH)
∴OD=OC,
∵∠AOB=60°,
∴△OCD是等边三角形;
(2)∵△OCD是等边三角形,OF是角平分线,
∴OE⊥DC,
∵∠AOB=60°,
∴∠AOE=∠BOE=30°,
∵∠ODF=60°,ED⊥OA,
∴∠EDF=30°,
∴DE=2EF=10,
∴OE=2DE=20.
【总结升华】本题考查等边三角形的判定和性质,角平分线的性质,三角形全等的判定和性质,30°的直角三角形的性质等,熟练掌握性质和定理是解题的关键。
举一反三:
【 等边三角形:例5】
【变式】如图, △ABC中, ∠ACB=90°, ∠ABC=60°, AB的中垂线交BC的延长线于D,交AC于E, 已知DE=2.则 AC的长为_________.
【答案】3;
提示:连接AD,证△ABD为等边三角形,则DE=AE=2,CE=1,所以AC=3.
【巩固练习】
一.选择题
1. (2019?陕西一模)已知:如图,在△ABC中,D为BC的中点,AD⊥BC,E为AD上一点,∠ABC=60°,∠ECD=40°,则∠ABE=( )
A.10° B.15° C.20° D.25°
2.以下叙述中不正确的是( ).
A.等边三角形的每条高线都是角平分线和中线;
B.有一个内角为60°的等腰三角形是等边三角形;
C.等腰三角形一定是锐角三角形;
D.在一个三角形中,如果有两条边相等,那么它们所对的角也相等;反之,在一个三角形中,如果有两个角相等,那么它们所对的边也相等.
3.(2019秋?荔湾区期末)如图,若△ABC是等边三角形,AB=6,BD是∠ABC的平分线,延长BC到E,使CE=CD,则BE=( )
A.7 B. 8 C. 9 D. 10
4. △ABC中三边为、、,满足关系式 (-)(-)(-)=0,则这个三角形一定为 ( )
A.等边三角形 B.等腰三角形
C.等腰钝角三角形 D.等腰直角三角形
5. 等边三角形的两条高线相交成钝角的度数是( )
A.105° B.120° C.135° D.150°
6. 如图,等边三角形ABC中,D为BC的中点,BE平分∠ABC交AD 于E,若△CDE的面积等于1,则△ABC的面积等于( )
A.2 B.4 C.6 D.12
二.填空题
7. (2019?黔南州)如图,在△ABC中,∠C=90°,∠B=30°,AB的垂直平分线ED交AB于点E,交BC于点D,若CD=3,则BD的长为 .
8.如图,△ABC为等边三角形,DC∥AB,AD⊥CD于D.若△ABC的周长为12,则CD =________.
9. 下列命题是真命题的是_________.
①有一个外角是120°的等腰三角形是等边三角形.
②有两个外角相等的等腰三角形是等边三角形.
③有一边上的高也是这边上的中线的等腰三角形是等边三角形.
④三个外角都相等的三角形是等边三角形.
10.△ABC为等边三角形,D、E、F分别在边BC、CA、AB上,且AE=CD=BF,则△DEF为_____三角形.
11.如图所示,△ABC为等边三角形,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,则四个结论正确的是 .
①P在∠A的平分线上; ②AS=AR;③QP∥AR;④△BRP≌△QSP.
12.如图,是等边三角形,点是边上任意一点,于点, 于点.若,则_____________.
三.解答题
13. 已知:如图,△ABD为等边三角形,△ACB为等腰三角形且∠ACB=90°,DE⊥AC交AC延长线于E,求证:DE=CE.
14.(2019秋?大英县校级期末)已知:等边△ABC和点P,设点P到△ABC的三边AB、AC、BC的距离分别为h1、h2、h3,△ABC的高为h.
(1)如图1,若点P在边BC上,证明:h1+h2=h.
(2)如图2,当点P在△ABC内时,猜想h1、h2、h3和h有什么关系?并证明你的结论.
(3)如图3,当点P在△ABC外时,h1、h2、h3和h有什么关系?(不需要证明)
15. 如图,直角△ACB中,∠ABC=90°,∠BAC=30°,而△ACD和△ABE都是等边三角形,AC,DE交于F.求证:FD=FE且CF=3AF.
【答案与解析】
选择题
1. 【答案】C;
【解析】∵D为BC的中点,AD⊥BC,∴EB=EC,AB=AC;
∴∠EBD=∠ECD,∠ABC=∠ACD.
又∵∠ABC=60°,∠ECD=40°,
∴∠ABE=60°﹣400=200.
2. 【答案】C;
【解析】等腰三角形顶角还可能是直角或钝角.
3. 【答案】C;
【解析】证明:∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,
∵BD是∠ABC的平分线,
∴AD=CD=AC,∠DBC=∠ABC=30°,
∵CE=CD,
∴CE=AC=3
∴BE=BC+CE=6+3=9.
故选C.
4. 【答案】B;
【解析】由题意=或=或=,这个三角形一定是等腰三角形.
5. 【答案】B;
【解析】等边△ABC的两条高线相交于O,∠OAB=∠OBA=30°,故∠AOB=120°.
6. 【答案】C;
【解析】AE=2DE,△ABC的面积是△CDE面积的6倍.
二.填空题
7. 【答案】6;
【解析】 ∵DE是AB的垂直平分线,
∴AD=BD,
∴∠DAE=∠B=30°,
∴∠ADC=60°,
∴∠CAD=30°,
∴AD为∠BAC的角平分线,
∵∠C=90°,DE⊥AB,
∴DE=CD=3,
∵∠B=30°,
∴BD=2DE=6.
8. 【答案】2;
【解析】在直角三角形中,30°的直角边等于斜边的一半.
9. 【答案】①④
【解析】②一般等腰三角形的两个底角的外角都相等;③等腰三角形底边上的高就是底边的中线.
10.【答案】等边;
【解析】利用SAS可以判定△EAF≌△FBD≌△DCE,从而可得,EF=FD=DE,即△DEF为等边三角形.
11.【答案】①②③④;
12.【答案】2;
【解析】BE=BD;CF=DC,(BD+DC)=2.
三.解答题
13.【解析】
证明:连接DC,
∵△ABD为等边三角形,
∴∠DAB=∠DBA=60°
又∵△ACB为等腰三角形且∠ACB=90°,
∴∠CAB=∠CBA=45°,∠BDC=∠ADC=30°
∴∠CBD=15°,∠DCB=180°-30°-15°=135°
又∵AC⊥BC,∴∠DCE=45°
∵DE⊥AC
∴ΔDEC为等腰直角三角形
∴DE=CE
14.【解析】
解:(1)如图1,连接AP,则 S△ABC=S△ABP+S△APC
∴BC?AM=AB?PD+AC?PF
即 BC?h=AB?h1+AC?h2
又∵△ABC是等边三角形
∴BC=AB=AC,
∴h=h1+h2.
(2)h=h1+h2+h3 ,理由如下:
如图2,连接AP、BP、CP,则 S△ABC=S△ABP+S△BPC+S△ACP
∴BC?AM=AB?PD+AC?PF+BC?PE
即BC?h=AB?h1+AC?h2+BC?h3
又∵△ABC是等边三角形,
∴BC=AB=AC.
∴h=h1+h2+h3.
(3)h=h1+h2﹣h3.
理由如下:如图3,连接PB,PC,PA
由三角形的面积公式得:S△ABC=S△PAB+S△PAC﹣S△PBC,
即BC?AM=AB?PD+AC?PE﹣BC?PF,
∵AB=BC=AC,
∴h1+h2﹣h3=h,
即h1+h2﹣h3=h.
15.【解析】
证明:作DG⊥AC于G,
∵△ACD和△ABE都是等边三角形,
∴∠CDG=30°,DC=AC,AB=AE,CG=AG
在△ABC与△DGC中
∴△ABC≌△DGC(AAS)
∴DG=AB=AE
在△DGF和△EAF中,
∴△DGF≌△EAF(AAS)
∴AF=GF,FD=FE
∵CG=AG,AF+GF=AG
∴CF=3AF.
