河北省邢台市2018-2019学年八年级(上)期末数学试卷含解析
文档属性
| 名称 | 河北省邢台市2018-2019学年八年级(上)期末数学试卷含解析 |  | |
| 格式 | zip | ||
| 文件大小 | 412.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-03 09:54:35 | ||
图片预览


文档简介
2018-2019学年八年级(上)期末数学试卷
一、选择题(本大题有14个小题,每小题3分,共42分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列式子,表示4的平方根的是( )
A. B.42 C.﹣ D.±
2.把8.973精确到十分位是( )
A.9 B.9.00 C.8.97 D.9.0
3.用反证法证明命题:“如图,如果AB∥CD,AB∥EF,那么CD∥EF”,证明的第一个步骤是( )
A.假定CD∥EF B.假定CD不平行于EF
C.已知AB∥EF D.假定AB不平行于EF
4.若是无理数,则a的值可以是( )
A. B.1 C.2 D.9
5.已知图中所有的小正方形都全等,若在右图中再添加一个全等的小正方形得到新的图形,使新图形是中心对称图形,则正确的添加方案是( )
A. B.
C. D.
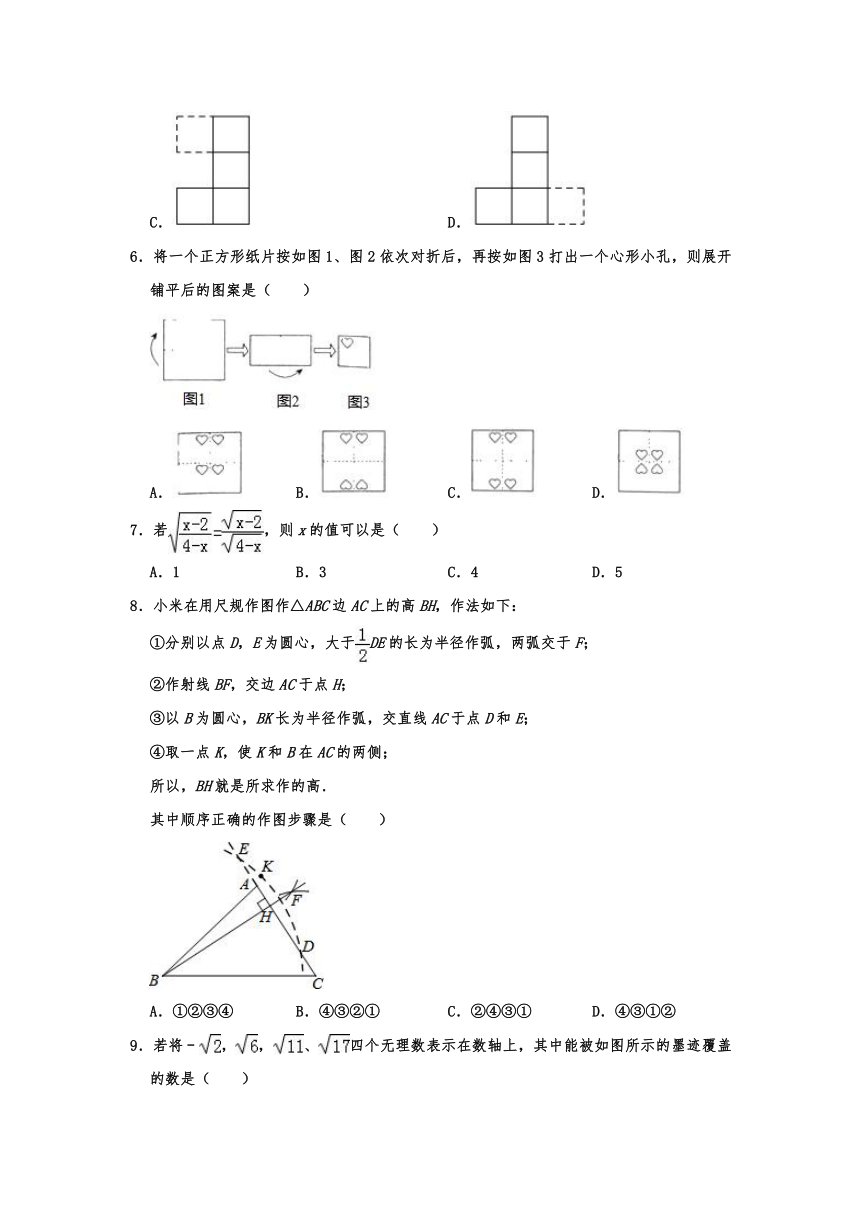
6.将一个正方形纸片按如图1、图2依次对折后,再按如图3打出一个心形小孔,则展开铺平后的图案是( )
A. B. C. D.
7.若,则x的值可以是( )
A.1 B.3 C.4 D.5
8.小米在用尺规作图作△ABC边AC上的高BH,作法如下:
①分别以点D,E为圆心,大于DE的长为半径作弧,两弧交于F;
②作射线BF,交边AC于点H;
③以B为圆心,BK长为半径作弧,交直线AC于点D和E;
④取一点K,使K和B在AC的两侧;
所以,BH就是所求作的高.
其中顺序正确的作图步骤是( )
A.①②③④ B.④③②① C.②④③① D.④③①②
9.若将﹣,,、四个无理数表示在数轴上,其中能被如图所示的墨迹覆盖的数是( )
A.﹣ B. C. D.
10.如图,是“赵爽弦图”,△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,如果EF=4,AH=12,那么AB等于( )
A.30 B.25 C.20 D.15
11.在将式子(m>0)化简时,
小明的方法是:;
小亮的方法是:;
小丽的方法是:.
则下列说法正确的是( )
A.小明、小亮的方法正确,小丽的方法不正确
B.小明、小丽的方法正确,小亮的方法不正确
C.小明、小亮、小丽的方法都正确
D.小明、小丽、小亮的方法都不正确
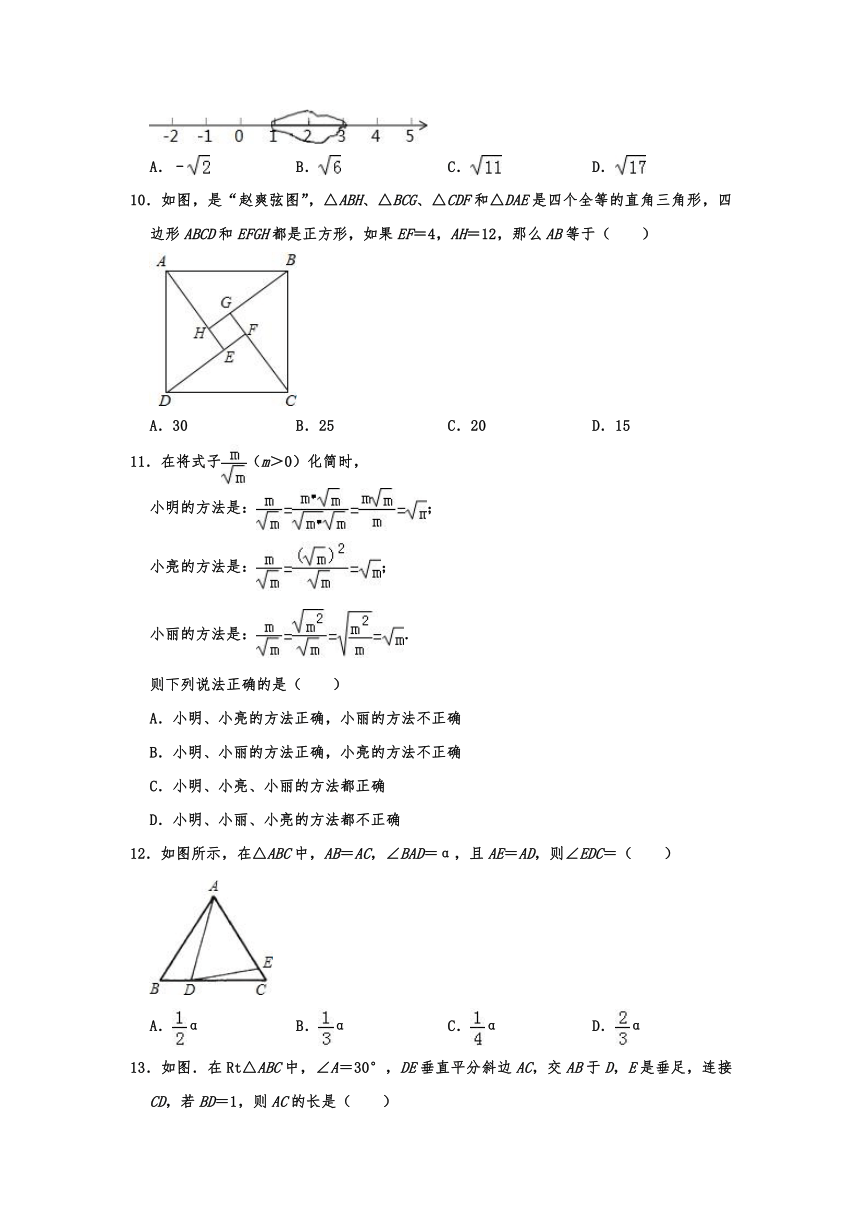
12.如图所示,在△ABC中,AB=AC,∠BAD=α,且AE=AD,则∠EDC=( )
A.α B.α C.α D.α
13.如图.在Rt△ABC中,∠A=30°,DE垂直平分斜边AC,交AB于D,E是垂足,连接CD,若BD=1,则AC的长是( )
A.2 B.2 C.4 D.4
14.如图,△ABC中,AB=AC=10,BC=8,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则△CDE的周长为( )
A.20 B.12 C.14 D.13
二、填空题(本大题有3个小题,每小题4分,共12分)
15.已知命题:“等角的补角相等.”写出它的逆命题: .
16.若,则括号中式子为 .
17.如图,在Rt△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,CD=2,则BC= .
三、解答题(本大题共7小题,共66分.解答应写出文字说明、证明过程或演算步骤)
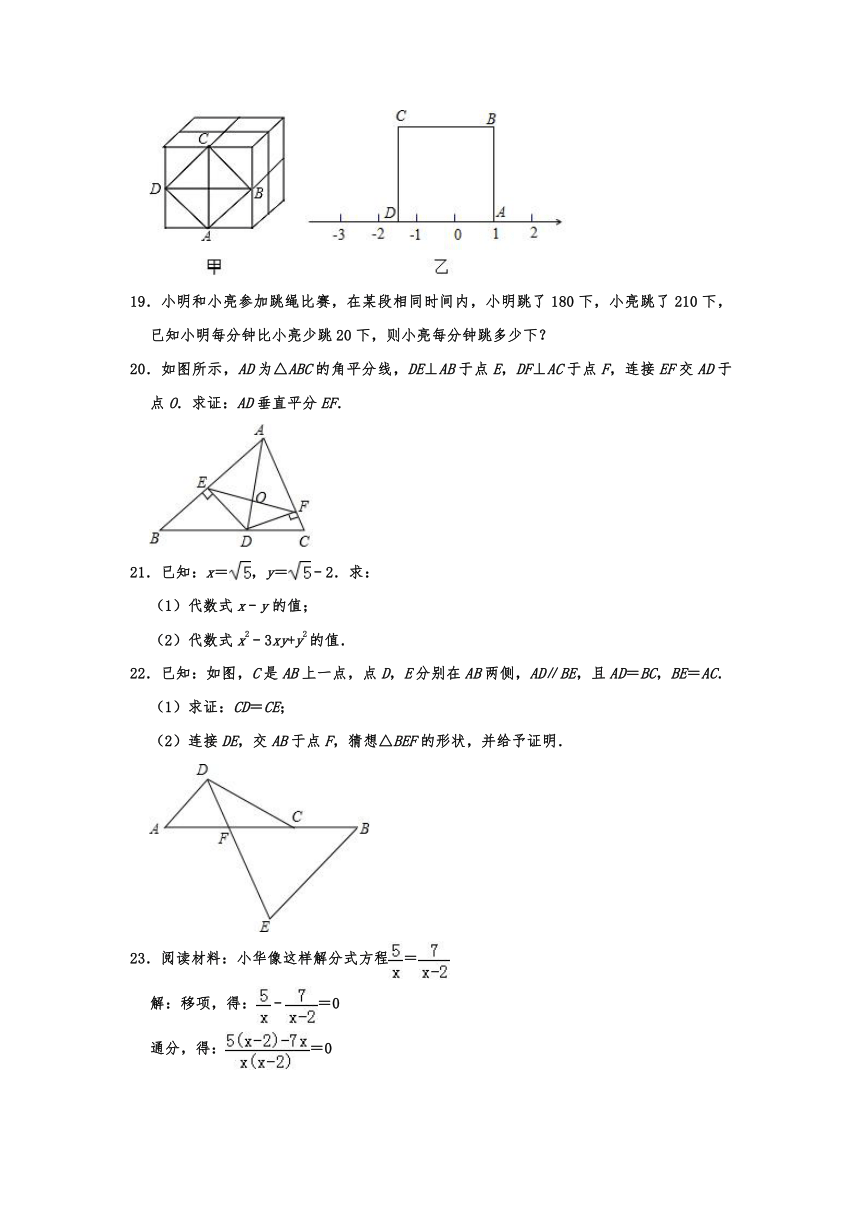
18.如图甲,这是由8个同样大小的立方体组成的魔方,总体积为64cm3.
(1)这个魔方的棱长为 cm;
(2)图甲中阴影部分是一个正方形ABCD,求这个正方形的边长;
(3)把正方形ABCD放置在数轴上,如图乙所示,使得点A与数1重合,则D在数轴上表示的数为 .
19.小明和小亮参加跳绳比赛,在某段相同时间内,小明跳了180下,小亮跳了210下,已知小明每分钟比小亮少跳20下,则小亮每分钟跳多少下?
20.如图所示,AD为△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,连接EF交AD于点O.求证:AD垂直平分EF.
21.已知:x=,y=﹣2.求:
(1)代数式x﹣y的值;
(2)代数式x2﹣3xy+y2的值.
22.已知:如图,C是AB上一点,点D,E分别在AB两侧,AD∥BE,且AD=BC,BE=AC.
(1)求证:CD=CE;
(2)连接DE,交AB于点F,猜想△BEF的形状,并给予证明.
23.阅读材料:小华像这样解分式方程=
解:移项,得:﹣=0
通分,得:=0
整理,得:=0
分子值取0,得:x+5=0
即:x=﹣5
经检验:x=﹣5是原分式方程的解.
(1)小华这种解分式方程的新方法,主要依据是 ;
(2)试用小华的方法解分式方程﹣=1
24.探究:已知,如图1,在△ABC中,∠ACB=90°,AC=6,BC=8,D是线段AB上一个动点.
(1)画出点D关于直线AC、BC的对称点M、N;
(2)在(1)的条件下,连接MN
①求证:M、C、N三点在同一条直线上;
②求MN的最小值.
应用:已知,如图2,在△ABC中,∠C=30°,AC=CB,AB=3,△ABC的面积为S,点D、E、F分别是AB、AC、BC上三个动点,请用含S的代数式直接表示△DEF的周长的最小值,并在图2中画出符合题意的图形.
参考答案与试题解析
一.选择题(共14小题)
1.下列式子,表示4的平方根的是( )
A. B.42 C.﹣ D.±
【分析】根据平方根的概念解答即可.
【解答】解:表示4的平方根的是,
故选:D.
2.把8.973精确到十分位是( )
A.9 B.9.00 C.8.97 D.9.0
【分析】根据近似数的精确度,把百分位上的数字4进行四舍五入即可.
【解答】解:把8.973精确到十分位是9.0,
故选:D.
3.用反证法证明命题:“如图,如果AB∥CD,AB∥EF,那么CD∥EF”,证明的第一个步骤是( )
A.假定CD∥EF B.假定CD不平行于EF
C.已知AB∥EF D.假定AB不平行于EF
【分析】根据要证CD∥EF,直接假设CD不平行于EF即可得出.
【解答】解:∵用反证法证明命题:如果AB∥CD,AB∥EF,那么CD∥EF.
∴证明的第一步应是:从结论反面出发,假设CD不平行于EF.
故选:B.
4.若是无理数,则a的值可以是( )
A. B.1 C.2 D.9
【分析】根据无理数的概念和算术平方根解答即可.
【解答】解:A、是有理数,错误;
B、是有理数,错误;
C、是无理数,正确;
D、是有理数,错误;
故选:C.
5.已知图中所有的小正方形都全等,若在右图中再添加一个全等的小正方形得到新的图形,使新图形是中心对称图形,则正确的添加方案是( )
A. B.
C. D.
【分析】直接利用中心对称图形的性质得出答案.
【解答】解:A、新图形不是中心对称图形,故此选项错误;
B、新图形是中心对称图形,故此选项正确;
C、新图形不是中心对称图形,故此选项错误;
D、新图形不是中心对称图形,故此选项错误;
故选:B.
6.将一个正方形纸片按如图1、图2依次对折后,再按如图3打出一个心形小孔,则展开铺平后的图案是( )
A. B. C. D.
【分析】依据轴对称的性质,将纸片依次展开还原,即可得到正确结论.
【解答】解:将图3展开可得小孔位于图2中虚线的左右两侧,且位于上边缘;
把图2展开可得小孔位于图1中虚线的上下两侧,且关于该虚线对称;
故选:B.
7.若,则x的值可以是( )
A.1 B.3 C.4 D.5
【分析】根据二次根式的有意义的条件解答即可.
【解答】解:若,
所以,
解得:2≤x<4,
故选:B.
8.小米在用尺规作图作△ABC边AC上的高BH,作法如下:
①分别以点D,E为圆心,大于DE的长为半径作弧,两弧交于F;
②作射线BF,交边AC于点H;
③以B为圆心,BK长为半径作弧,交直线AC于点D和E;
④取一点K,使K和B在AC的两侧;
所以,BH就是所求作的高.
其中顺序正确的作图步骤是( )
A.①②③④ B.④③②① C.②④③① D.④③①②
【分析】根据直线外一点作已知直线的垂线的方法作BH⊥AC即可.
【解答】解:用尺规作图作△ABC边AC上的高BH,作法如下:
取一点K,使K和B在AC的两侧;
以B为圆心,BK长为半径作弧,交直线AC于点D和E;
分别以点D,E为圆心,大于DE的长为半径作弧,两弧交于F;
作射线BF,交边AC于点H;
所以,BH就是所求作的高.
故正确的作图步骤是④③①②.
故选:D.
9.若将﹣,,、四个无理数表示在数轴上,其中能被如图所示的墨迹覆盖的数是( )
A.﹣ B. C. D.
【分析】先估算出各数,再根据实数与数轴的关系即可得出结论.
【解答】解:﹣是负数,在原点的左侧,不符合题意;
<<6<,即2<<3,符合题意;
>,即>3,在墨迹覆盖处的右边,不符合题意;
>,即>4,在墨迹覆盖处的右边,不符合题意;
故选:B.
10.如图,是“赵爽弦图”,△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,如果EF=4,AH=12,那么AB等于( )
A.30 B.25 C.20 D.15
【分析】在直角三角形AHB中,利用勾股定理进行解答即可.
【解答】解:∵△ABH≌△BCG,
∴BG=AH=12,
∵四边形EFGH都是正方形,
∴HG=EF=4,
∴BH=16,
∴在直角三角形AHB中,由勾股定理得到:AB===20.
故选:C.
11.在将式子(m>0)化简时,
小明的方法是:;
小亮的方法是:;
小丽的方法是:.
则下列说法正确的是( )
A.小明、小亮的方法正确,小丽的方法不正确
B.小明、小丽的方法正确,小亮的方法不正确
C.小明、小亮、小丽的方法都正确
D.小明、小丽、小亮的方法都不正确
【分析】小明的方法为原式分子分母乘以有理化因式,化简得到结果;小亮的方法为将分子利用二次根式性质化简,约分即可得到结果;小丽得方法为分子利用二次根式性质化简,再利用二次根式除法法则逆运算变形,计算即可得到结果.
【解答】解:在将式子(m>0)化简时,
小明的方法是:===,正确;
小亮的方法是:==,正确;
小丽的方法是:===,正确,
则小明、小亮、小丽的方法都正确.
故选:C.
12.如图所示,在△ABC中,AB=AC,∠BAD=α,且AE=AD,则∠EDC=( )
A.α B.α C.α D.α
【分析】根据等边对等角,和三角形的外角性质列出等式整理即可得出结论.
【解答】解:根据题意:在△ABC中,AB=AC
∴∠B=∠C
∵AE=AD
∴∠ADE=∠AED,即∠B+∠α﹣∠EDC=∠C+∠EDC
化简可得:∠α=2∠EDC
∴∠EDC=α.
故选:A.
13.如图.在Rt△ABC中,∠A=30°,DE垂直平分斜边AC,交AB于D,E是垂足,连接CD,若BD=1,则AC的长是( )
A.2 B.2 C.4 D.4
【分析】求出∠ACB,根据线段垂直平分线求出AD=CD,求出∠ACD、∠DCB,求出CD、AD、AB,由勾股定理求出BC,再求出AC即可.
【解答】解:∵∠A=30°,∠B=90°,
∴∠ACB=180°﹣30°﹣90°=60°,
∵DE垂直平分斜边AC,
∴AD=CD,
∴∠A=∠ACD=30°,
∴∠DCB=60°﹣30°=30°,
∵BD=1,
∴CD=2=AD,
∴AB=1+2=3,
在△BCD中,由勾股定理得:CB=,
在△ABC中,由勾股定理得:AC==2,
故选:A.
14.如图,△ABC中,AB=AC=10,BC=8,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则△CDE的周长为( )
A.20 B.12 C.14 D.13
【分析】根据等腰三角形三线合一的性质可得AD⊥BC,CD=BD,再根据直角三角形斜边上的中线等于斜边的一半可得DE=CE=AC,然后根据三角形的周长公式列式计算即可得解.
【解答】解:∵AB=AC,AD平分∠BAC,BC=8,
∴AD⊥BC,CD=BD=BC=4,
∵点E为AC的中点,
∴DE=CE=AC=5,
∴△CDE的周长=CD+DE+CE=4+5+5=14.
故选:C.
二.填空题(共3小题)
15.已知命题:“等角的补角相等.”写出它的逆命题: 如果两个角的补角相等,那么这两个角相等 .
【分析】交换命题的题设和结论即可写出该命题的逆命题.
【解答】解:等角的补角相等的逆命题为:如果两个角的补角相等,那么这两个角相等,
故答案为:如果两个角的补角相等,那么这两个角相等.
16.若,则括号中式子为 ﹣2x(x+1) .
【分析】根据分式的除法法则计算,得到答案.
【解答】解:÷=?(x+1)(x﹣1)=﹣2x(x+1),
故答案为:﹣2x(x+1).
17.如图,在Rt△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,CD=2,则BC= 6 .
【分析】作DE⊥AB于E,根据角平分线的性质得到DE=CD=2,根据直角三角形的性质得到BD=2DE=4,结合图形计算即可.
【解答】解:作DE⊥AB于E,
∵AD是△ABC的角平分线,∠C=90°,DE⊥AB,
∴DE=CD=2,
∵DE⊥AB,∠B=30°,
∴BD=2DE=4,
∴BC=CD+BD=6,
故答案为:6.
三.解答题(共7小题)
18.如图甲,这是由8个同样大小的立方体组成的魔方,总体积为64cm3.
(1)这个魔方的棱长为 4 cm;
(2)图甲中阴影部分是一个正方形ABCD,求这个正方形的边长;
(3)把正方形ABCD放置在数轴上,如图乙所示,使得点A与数1重合,则D在数轴上表示的数为 1﹣2 .
【分析】(1)魔方是个正方体,正方体的体积等于棱长的三次方;
(2)这个正方形ABCD的边长是小立方体一个面的对角线的长度;
(3)点D表示的数是负数,它的绝对值比正方形ABCD的边长少1.
【解答】解:(1)设魔方的棱长为acm,根据题意得 a3=64
∴a=4
故答案为4.
(2)设小正方体的棱长为bcm,根据题意得 8b3=64
∴b=2
∴所以根据勾股定理得 CD2=22+22
∴CD=2
答:这个正方形的边长是2cm.
(3)由(2)知,AD=2
∴点D对应的数的绝对值是2﹣1
∵点D对应的数是负数
∴点D对应的数是1﹣2
故答案为1﹣2.
19.小明和小亮参加跳绳比赛,在某段相同时间内,小明跳了180下,小亮跳了210下,已知小明每分钟比小亮少跳20下,则小亮每分钟跳多少下?
【分析】设小亮每分钟跳x下,则小明每分钟跳(x﹣20)下,根据小明跳180下与小亮跳210下的时间相等建立方程求出其解即可.
【解答】解:设小亮每分钟跳x下,则小明每分钟跳(x﹣20)下,由题意,得
解得:x=140
经检验:x=140是原方程的解,
答:小亮每分钟跳140下.
20.如图所示,AD为△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,连接EF交AD于点O.求证:AD垂直平分EF.
【分析】由AD为△ABC的角平分线,得到DE=DF,推出∠AEF和∠AFE相等,得到AE=AF,即可推出结论.
【解答】证明:∵AD为△ABC的角平分线,DE⊥AB,DF⊥AC,
∴DE=DF,∠AED=∠AFD=90°,
∴∠DEF=∠DFE,
∴∠AEF=∠AFE,
∴AE=AF
∴点A、D都在EF的垂直平分线上,
∴AD垂直平分EF
21.已知:x=,y=﹣2.求:
(1)代数式x﹣y的值;
(2)代数式x2﹣3xy+y2的值.
【分析】(1)将x、y的值代入计算可得;
(2)将x、y的值代入原式=(x﹣y)2﹣xy计算可得.
【解答】解:(1)∵x=,y=﹣2,
∴x﹣y=﹣+2=2;
(2)原式=(x﹣y)2﹣xy
=(﹣+2)2﹣(﹣2)
=4﹣5+2
=2﹣1.
22.已知:如图,C是AB上一点,点D,E分别在AB两侧,AD∥BE,且AD=BC,BE=AC.
(1)求证:CD=CE;
(2)连接DE,交AB于点F,猜想△BEF的形状,并给予证明.
【分析】(1)连接CE,由平行线的性质,结合条件可证明△ADC≌△BCE,可证明CD=CE;
(2)由(1)中的全等可得∠CDE=∠CED,∠ACD=∠BEC,可证明∠BFE=∠BEF,可证明△BEF为等腰三角形.
【解答】(1)证明:如图,连接CE,
∵AD∥BE,
∴∠A=∠B,
在△ADC和△BCE中
∴△ADC≌△BCE(SAS),
∴CD=CE;
(2)解:△BEF为等腰三角形,证明如下:
由(1)可知CD=CE,
∴∠CDE=∠CED,
由(1)可知△ADC≌△BEC,
∴∠ACD=∠BEC,
∴∠CDE+∠ACD=∠CED+∠BEC,
即∠BFE=∠BED,
∴BE=BF,
∴△BEF是等腰三角形.
23.阅读材料:小华像这样解分式方程=
解:移项,得:﹣=0
通分,得:=0
整理,得:=0
分子值取0,得:x+5=0
即:x=﹣5
经检验:x=﹣5是原分式方程的解.
(1)小华这种解分式方程的新方法,主要依据是 分式的值为0即分子为0且分母不为0 ;
(2)试用小华的方法解分式方程﹣=1
【分析】(1)根据分式的值为0即分子为0且分母不为0可得;
(2)移项后,通分、根据分式的加减法则计算左边,再由(1)中结论得出关于x的方程,解之求得x的值,最后检验即可得.
【解答】解:(1)小华这种解分式方程的新方法,主要依据是分式的值为0即分子为0且分母不为0,
故答案为:分式的值为0即分子为0且分母不为0.
(2)﹣﹣1=0,
﹣﹣=0,
=0,
=0,
则﹣4(x+2)=0,
解得:x=﹣2,
检验:x=﹣2时,分母为0,分式无意义,
所以x=﹣2是增根,原分式方程无解.
24.探究:已知,如图1,在△ABC中,∠ACB=90°,AC=6,BC=8,D是线段AB上一个动点.
(1)画出点D关于直线AC、BC的对称点M、N;
(2)在(1)的条件下,连接MN
①求证:M、C、N三点在同一条直线上;
②求MN的最小值.
应用:已知,如图2,在△ABC中,∠C=30°,AC=CB,AB=3,△ABC的面积为S,点D、E、F分别是AB、AC、BC上三个动点,请用含S的代数式直接表示△DEF的周长的最小值,并在图2中画出符合题意的图形.
【分析】探究:(1)根据要求画出图形即可;
(2)①想办法证明∠MCN=180°即可;
②由题意可知MN=2CD,当CD⊥AB时,CD的值最小,即MN的值最小;
应用:如图2中,设D是AB上任意一点,作点D关于直线AC的对称点D′,点D关于直线BC的对称点D″,连接D′D″交AC于E,交BC于F.作CH⊥AB于H.由△DEF的周长=DE+EF+DF=D′E+EF+FD″=D′D″=CD,推出CD的值最小时,△DEF的周长最小,由此即可解决问题;
【解答】探究:(1)解:如图1中,点M,N即为所求;
(2)①证明:连接CD,
由对称的性质可知:∠ACD=∠ACM,∠BCD=∠BCN,
∵∠ACD+∠BCD=90°,
∴∠MCD+∠NCD=2(∠ACD+∠BCD)=180°,
∴M,C,N共线.
②解:∵CM=CD,CN=CD,
∴MN=CM+CN=2CD,
∴当CD最短时,MN的值最小,
∵CD⊥AB时,垂线段最短,
∴CD的最小值===,
∴MN的最小值是;
应用:解:如图2中,设D是AB上任意一点,作点D关于直线AC的对称点D′,点D关于直线BC的对称点D″,连接D′D″交AC于E,交BC于F.作CH⊥AB于H.
由对称的性质可知:CD=CD′=CD″,ED=ED′,FD=FD″,∠ACD=∠ACD′,∠BCD=∠BCD″,
∴∠D′CD″=2∠ACB=60°,
∴△D′CD″是等边三角形,
∴D′D″=CD′=CD,
∵△DEF的周长=DE+EF+DF=D′E+EF+FD″=D′D″=CD,
∴CD的值最小时,△DEF的周长最小,
当CD与CH重合时,CD的值最小,
∵?AB?CH=S,
∴CH=,
∴△DEF的周长的最小值为.
一、选择题(本大题有14个小题,每小题3分,共42分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列式子,表示4的平方根的是( )
A. B.42 C.﹣ D.±
2.把8.973精确到十分位是( )
A.9 B.9.00 C.8.97 D.9.0
3.用反证法证明命题:“如图,如果AB∥CD,AB∥EF,那么CD∥EF”,证明的第一个步骤是( )
A.假定CD∥EF B.假定CD不平行于EF
C.已知AB∥EF D.假定AB不平行于EF
4.若是无理数,则a的值可以是( )
A. B.1 C.2 D.9
5.已知图中所有的小正方形都全等,若在右图中再添加一个全等的小正方形得到新的图形,使新图形是中心对称图形,则正确的添加方案是( )
A. B.
C. D.
6.将一个正方形纸片按如图1、图2依次对折后,再按如图3打出一个心形小孔,则展开铺平后的图案是( )
A. B. C. D.
7.若,则x的值可以是( )
A.1 B.3 C.4 D.5
8.小米在用尺规作图作△ABC边AC上的高BH,作法如下:
①分别以点D,E为圆心,大于DE的长为半径作弧,两弧交于F;
②作射线BF,交边AC于点H;
③以B为圆心,BK长为半径作弧,交直线AC于点D和E;
④取一点K,使K和B在AC的两侧;
所以,BH就是所求作的高.
其中顺序正确的作图步骤是( )
A.①②③④ B.④③②① C.②④③① D.④③①②
9.若将﹣,,、四个无理数表示在数轴上,其中能被如图所示的墨迹覆盖的数是( )
A.﹣ B. C. D.
10.如图,是“赵爽弦图”,△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,如果EF=4,AH=12,那么AB等于( )
A.30 B.25 C.20 D.15
11.在将式子(m>0)化简时,
小明的方法是:;
小亮的方法是:;
小丽的方法是:.
则下列说法正确的是( )
A.小明、小亮的方法正确,小丽的方法不正确
B.小明、小丽的方法正确,小亮的方法不正确
C.小明、小亮、小丽的方法都正确
D.小明、小丽、小亮的方法都不正确
12.如图所示,在△ABC中,AB=AC,∠BAD=α,且AE=AD,则∠EDC=( )
A.α B.α C.α D.α
13.如图.在Rt△ABC中,∠A=30°,DE垂直平分斜边AC,交AB于D,E是垂足,连接CD,若BD=1,则AC的长是( )
A.2 B.2 C.4 D.4
14.如图,△ABC中,AB=AC=10,BC=8,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则△CDE的周长为( )
A.20 B.12 C.14 D.13
二、填空题(本大题有3个小题,每小题4分,共12分)
15.已知命题:“等角的补角相等.”写出它的逆命题: .
16.若,则括号中式子为 .
17.如图,在Rt△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,CD=2,则BC= .
三、解答题(本大题共7小题,共66分.解答应写出文字说明、证明过程或演算步骤)
18.如图甲,这是由8个同样大小的立方体组成的魔方,总体积为64cm3.
(1)这个魔方的棱长为 cm;
(2)图甲中阴影部分是一个正方形ABCD,求这个正方形的边长;
(3)把正方形ABCD放置在数轴上,如图乙所示,使得点A与数1重合,则D在数轴上表示的数为 .
19.小明和小亮参加跳绳比赛,在某段相同时间内,小明跳了180下,小亮跳了210下,已知小明每分钟比小亮少跳20下,则小亮每分钟跳多少下?
20.如图所示,AD为△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,连接EF交AD于点O.求证:AD垂直平分EF.
21.已知:x=,y=﹣2.求:
(1)代数式x﹣y的值;
(2)代数式x2﹣3xy+y2的值.
22.已知:如图,C是AB上一点,点D,E分别在AB两侧,AD∥BE,且AD=BC,BE=AC.
(1)求证:CD=CE;
(2)连接DE,交AB于点F,猜想△BEF的形状,并给予证明.
23.阅读材料:小华像这样解分式方程=
解:移项,得:﹣=0
通分,得:=0
整理,得:=0
分子值取0,得:x+5=0
即:x=﹣5
经检验:x=﹣5是原分式方程的解.
(1)小华这种解分式方程的新方法,主要依据是 ;
(2)试用小华的方法解分式方程﹣=1
24.探究:已知,如图1,在△ABC中,∠ACB=90°,AC=6,BC=8,D是线段AB上一个动点.
(1)画出点D关于直线AC、BC的对称点M、N;
(2)在(1)的条件下,连接MN
①求证:M、C、N三点在同一条直线上;
②求MN的最小值.
应用:已知,如图2,在△ABC中,∠C=30°,AC=CB,AB=3,△ABC的面积为S,点D、E、F分别是AB、AC、BC上三个动点,请用含S的代数式直接表示△DEF的周长的最小值,并在图2中画出符合题意的图形.
参考答案与试题解析
一.选择题(共14小题)
1.下列式子,表示4的平方根的是( )
A. B.42 C.﹣ D.±
【分析】根据平方根的概念解答即可.
【解答】解:表示4的平方根的是,
故选:D.
2.把8.973精确到十分位是( )
A.9 B.9.00 C.8.97 D.9.0
【分析】根据近似数的精确度,把百分位上的数字4进行四舍五入即可.
【解答】解:把8.973精确到十分位是9.0,
故选:D.
3.用反证法证明命题:“如图,如果AB∥CD,AB∥EF,那么CD∥EF”,证明的第一个步骤是( )
A.假定CD∥EF B.假定CD不平行于EF
C.已知AB∥EF D.假定AB不平行于EF
【分析】根据要证CD∥EF,直接假设CD不平行于EF即可得出.
【解答】解:∵用反证法证明命题:如果AB∥CD,AB∥EF,那么CD∥EF.
∴证明的第一步应是:从结论反面出发,假设CD不平行于EF.
故选:B.
4.若是无理数,则a的值可以是( )
A. B.1 C.2 D.9
【分析】根据无理数的概念和算术平方根解答即可.
【解答】解:A、是有理数,错误;
B、是有理数,错误;
C、是无理数,正确;
D、是有理数,错误;
故选:C.
5.已知图中所有的小正方形都全等,若在右图中再添加一个全等的小正方形得到新的图形,使新图形是中心对称图形,则正确的添加方案是( )
A. B.
C. D.
【分析】直接利用中心对称图形的性质得出答案.
【解答】解:A、新图形不是中心对称图形,故此选项错误;
B、新图形是中心对称图形,故此选项正确;
C、新图形不是中心对称图形,故此选项错误;
D、新图形不是中心对称图形,故此选项错误;
故选:B.
6.将一个正方形纸片按如图1、图2依次对折后,再按如图3打出一个心形小孔,则展开铺平后的图案是( )
A. B. C. D.
【分析】依据轴对称的性质,将纸片依次展开还原,即可得到正确结论.
【解答】解:将图3展开可得小孔位于图2中虚线的左右两侧,且位于上边缘;
把图2展开可得小孔位于图1中虚线的上下两侧,且关于该虚线对称;
故选:B.
7.若,则x的值可以是( )
A.1 B.3 C.4 D.5
【分析】根据二次根式的有意义的条件解答即可.
【解答】解:若,
所以,
解得:2≤x<4,
故选:B.
8.小米在用尺规作图作△ABC边AC上的高BH,作法如下:
①分别以点D,E为圆心,大于DE的长为半径作弧,两弧交于F;
②作射线BF,交边AC于点H;
③以B为圆心,BK长为半径作弧,交直线AC于点D和E;
④取一点K,使K和B在AC的两侧;
所以,BH就是所求作的高.
其中顺序正确的作图步骤是( )
A.①②③④ B.④③②① C.②④③① D.④③①②
【分析】根据直线外一点作已知直线的垂线的方法作BH⊥AC即可.
【解答】解:用尺规作图作△ABC边AC上的高BH,作法如下:
取一点K,使K和B在AC的两侧;
以B为圆心,BK长为半径作弧,交直线AC于点D和E;
分别以点D,E为圆心,大于DE的长为半径作弧,两弧交于F;
作射线BF,交边AC于点H;
所以,BH就是所求作的高.
故正确的作图步骤是④③①②.
故选:D.
9.若将﹣,,、四个无理数表示在数轴上,其中能被如图所示的墨迹覆盖的数是( )
A.﹣ B. C. D.
【分析】先估算出各数,再根据实数与数轴的关系即可得出结论.
【解答】解:﹣是负数,在原点的左侧,不符合题意;
<<6<,即2<<3,符合题意;
>,即>3,在墨迹覆盖处的右边,不符合题意;
>,即>4,在墨迹覆盖处的右边,不符合题意;
故选:B.
10.如图,是“赵爽弦图”,△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,如果EF=4,AH=12,那么AB等于( )
A.30 B.25 C.20 D.15
【分析】在直角三角形AHB中,利用勾股定理进行解答即可.
【解答】解:∵△ABH≌△BCG,
∴BG=AH=12,
∵四边形EFGH都是正方形,
∴HG=EF=4,
∴BH=16,
∴在直角三角形AHB中,由勾股定理得到:AB===20.
故选:C.
11.在将式子(m>0)化简时,
小明的方法是:;
小亮的方法是:;
小丽的方法是:.
则下列说法正确的是( )
A.小明、小亮的方法正确,小丽的方法不正确
B.小明、小丽的方法正确,小亮的方法不正确
C.小明、小亮、小丽的方法都正确
D.小明、小丽、小亮的方法都不正确
【分析】小明的方法为原式分子分母乘以有理化因式,化简得到结果;小亮的方法为将分子利用二次根式性质化简,约分即可得到结果;小丽得方法为分子利用二次根式性质化简,再利用二次根式除法法则逆运算变形,计算即可得到结果.
【解答】解:在将式子(m>0)化简时,
小明的方法是:===,正确;
小亮的方法是:==,正确;
小丽的方法是:===,正确,
则小明、小亮、小丽的方法都正确.
故选:C.
12.如图所示,在△ABC中,AB=AC,∠BAD=α,且AE=AD,则∠EDC=( )
A.α B.α C.α D.α
【分析】根据等边对等角,和三角形的外角性质列出等式整理即可得出结论.
【解答】解:根据题意:在△ABC中,AB=AC
∴∠B=∠C
∵AE=AD
∴∠ADE=∠AED,即∠B+∠α﹣∠EDC=∠C+∠EDC
化简可得:∠α=2∠EDC
∴∠EDC=α.
故选:A.
13.如图.在Rt△ABC中,∠A=30°,DE垂直平分斜边AC,交AB于D,E是垂足,连接CD,若BD=1,则AC的长是( )
A.2 B.2 C.4 D.4
【分析】求出∠ACB,根据线段垂直平分线求出AD=CD,求出∠ACD、∠DCB,求出CD、AD、AB,由勾股定理求出BC,再求出AC即可.
【解答】解:∵∠A=30°,∠B=90°,
∴∠ACB=180°﹣30°﹣90°=60°,
∵DE垂直平分斜边AC,
∴AD=CD,
∴∠A=∠ACD=30°,
∴∠DCB=60°﹣30°=30°,
∵BD=1,
∴CD=2=AD,
∴AB=1+2=3,
在△BCD中,由勾股定理得:CB=,
在△ABC中,由勾股定理得:AC==2,
故选:A.
14.如图,△ABC中,AB=AC=10,BC=8,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则△CDE的周长为( )
A.20 B.12 C.14 D.13
【分析】根据等腰三角形三线合一的性质可得AD⊥BC,CD=BD,再根据直角三角形斜边上的中线等于斜边的一半可得DE=CE=AC,然后根据三角形的周长公式列式计算即可得解.
【解答】解:∵AB=AC,AD平分∠BAC,BC=8,
∴AD⊥BC,CD=BD=BC=4,
∵点E为AC的中点,
∴DE=CE=AC=5,
∴△CDE的周长=CD+DE+CE=4+5+5=14.
故选:C.
二.填空题(共3小题)
15.已知命题:“等角的补角相等.”写出它的逆命题: 如果两个角的补角相等,那么这两个角相等 .
【分析】交换命题的题设和结论即可写出该命题的逆命题.
【解答】解:等角的补角相等的逆命题为:如果两个角的补角相等,那么这两个角相等,
故答案为:如果两个角的补角相等,那么这两个角相等.
16.若,则括号中式子为 ﹣2x(x+1) .
【分析】根据分式的除法法则计算,得到答案.
【解答】解:÷=?(x+1)(x﹣1)=﹣2x(x+1),
故答案为:﹣2x(x+1).
17.如图,在Rt△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,CD=2,则BC= 6 .
【分析】作DE⊥AB于E,根据角平分线的性质得到DE=CD=2,根据直角三角形的性质得到BD=2DE=4,结合图形计算即可.
【解答】解:作DE⊥AB于E,
∵AD是△ABC的角平分线,∠C=90°,DE⊥AB,
∴DE=CD=2,
∵DE⊥AB,∠B=30°,
∴BD=2DE=4,
∴BC=CD+BD=6,
故答案为:6.
三.解答题(共7小题)
18.如图甲,这是由8个同样大小的立方体组成的魔方,总体积为64cm3.
(1)这个魔方的棱长为 4 cm;
(2)图甲中阴影部分是一个正方形ABCD,求这个正方形的边长;
(3)把正方形ABCD放置在数轴上,如图乙所示,使得点A与数1重合,则D在数轴上表示的数为 1﹣2 .
【分析】(1)魔方是个正方体,正方体的体积等于棱长的三次方;
(2)这个正方形ABCD的边长是小立方体一个面的对角线的长度;
(3)点D表示的数是负数,它的绝对值比正方形ABCD的边长少1.
【解答】解:(1)设魔方的棱长为acm,根据题意得 a3=64
∴a=4
故答案为4.
(2)设小正方体的棱长为bcm,根据题意得 8b3=64
∴b=2
∴所以根据勾股定理得 CD2=22+22
∴CD=2
答:这个正方形的边长是2cm.
(3)由(2)知,AD=2
∴点D对应的数的绝对值是2﹣1
∵点D对应的数是负数
∴点D对应的数是1﹣2
故答案为1﹣2.
19.小明和小亮参加跳绳比赛,在某段相同时间内,小明跳了180下,小亮跳了210下,已知小明每分钟比小亮少跳20下,则小亮每分钟跳多少下?
【分析】设小亮每分钟跳x下,则小明每分钟跳(x﹣20)下,根据小明跳180下与小亮跳210下的时间相等建立方程求出其解即可.
【解答】解:设小亮每分钟跳x下,则小明每分钟跳(x﹣20)下,由题意,得
解得:x=140
经检验:x=140是原方程的解,
答:小亮每分钟跳140下.
20.如图所示,AD为△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,连接EF交AD于点O.求证:AD垂直平分EF.
【分析】由AD为△ABC的角平分线,得到DE=DF,推出∠AEF和∠AFE相等,得到AE=AF,即可推出结论.
【解答】证明:∵AD为△ABC的角平分线,DE⊥AB,DF⊥AC,
∴DE=DF,∠AED=∠AFD=90°,
∴∠DEF=∠DFE,
∴∠AEF=∠AFE,
∴AE=AF
∴点A、D都在EF的垂直平分线上,
∴AD垂直平分EF
21.已知:x=,y=﹣2.求:
(1)代数式x﹣y的值;
(2)代数式x2﹣3xy+y2的值.
【分析】(1)将x、y的值代入计算可得;
(2)将x、y的值代入原式=(x﹣y)2﹣xy计算可得.
【解答】解:(1)∵x=,y=﹣2,
∴x﹣y=﹣+2=2;
(2)原式=(x﹣y)2﹣xy
=(﹣+2)2﹣(﹣2)
=4﹣5+2
=2﹣1.
22.已知:如图,C是AB上一点,点D,E分别在AB两侧,AD∥BE,且AD=BC,BE=AC.
(1)求证:CD=CE;
(2)连接DE,交AB于点F,猜想△BEF的形状,并给予证明.
【分析】(1)连接CE,由平行线的性质,结合条件可证明△ADC≌△BCE,可证明CD=CE;
(2)由(1)中的全等可得∠CDE=∠CED,∠ACD=∠BEC,可证明∠BFE=∠BEF,可证明△BEF为等腰三角形.
【解答】(1)证明:如图,连接CE,
∵AD∥BE,
∴∠A=∠B,
在△ADC和△BCE中
∴△ADC≌△BCE(SAS),
∴CD=CE;
(2)解:△BEF为等腰三角形,证明如下:
由(1)可知CD=CE,
∴∠CDE=∠CED,
由(1)可知△ADC≌△BEC,
∴∠ACD=∠BEC,
∴∠CDE+∠ACD=∠CED+∠BEC,
即∠BFE=∠BED,
∴BE=BF,
∴△BEF是等腰三角形.
23.阅读材料:小华像这样解分式方程=
解:移项,得:﹣=0
通分,得:=0
整理,得:=0
分子值取0,得:x+5=0
即:x=﹣5
经检验:x=﹣5是原分式方程的解.
(1)小华这种解分式方程的新方法,主要依据是 分式的值为0即分子为0且分母不为0 ;
(2)试用小华的方法解分式方程﹣=1
【分析】(1)根据分式的值为0即分子为0且分母不为0可得;
(2)移项后,通分、根据分式的加减法则计算左边,再由(1)中结论得出关于x的方程,解之求得x的值,最后检验即可得.
【解答】解:(1)小华这种解分式方程的新方法,主要依据是分式的值为0即分子为0且分母不为0,
故答案为:分式的值为0即分子为0且分母不为0.
(2)﹣﹣1=0,
﹣﹣=0,
=0,
=0,
则﹣4(x+2)=0,
解得:x=﹣2,
检验:x=﹣2时,分母为0,分式无意义,
所以x=﹣2是增根,原分式方程无解.
24.探究:已知,如图1,在△ABC中,∠ACB=90°,AC=6,BC=8,D是线段AB上一个动点.
(1)画出点D关于直线AC、BC的对称点M、N;
(2)在(1)的条件下,连接MN
①求证:M、C、N三点在同一条直线上;
②求MN的最小值.
应用:已知,如图2,在△ABC中,∠C=30°,AC=CB,AB=3,△ABC的面积为S,点D、E、F分别是AB、AC、BC上三个动点,请用含S的代数式直接表示△DEF的周长的最小值,并在图2中画出符合题意的图形.
【分析】探究:(1)根据要求画出图形即可;
(2)①想办法证明∠MCN=180°即可;
②由题意可知MN=2CD,当CD⊥AB时,CD的值最小,即MN的值最小;
应用:如图2中,设D是AB上任意一点,作点D关于直线AC的对称点D′,点D关于直线BC的对称点D″,连接D′D″交AC于E,交BC于F.作CH⊥AB于H.由△DEF的周长=DE+EF+DF=D′E+EF+FD″=D′D″=CD,推出CD的值最小时,△DEF的周长最小,由此即可解决问题;
【解答】探究:(1)解:如图1中,点M,N即为所求;
(2)①证明:连接CD,
由对称的性质可知:∠ACD=∠ACM,∠BCD=∠BCN,
∵∠ACD+∠BCD=90°,
∴∠MCD+∠NCD=2(∠ACD+∠BCD)=180°,
∴M,C,N共线.
②解:∵CM=CD,CN=CD,
∴MN=CM+CN=2CD,
∴当CD最短时,MN的值最小,
∵CD⊥AB时,垂线段最短,
∴CD的最小值===,
∴MN的最小值是;
应用:解:如图2中,设D是AB上任意一点,作点D关于直线AC的对称点D′,点D关于直线BC的对称点D″,连接D′D″交AC于E,交BC于F.作CH⊥AB于H.
由对称的性质可知:CD=CD′=CD″,ED=ED′,FD=FD″,∠ACD=∠ACD′,∠BCD=∠BCD″,
∴∠D′CD″=2∠ACB=60°,
∴△D′CD″是等边三角形,
∴D′D″=CD′=CD,
∵△DEF的周长=DE+EF+DF=D′E+EF+FD″=D′D″=CD,
∴CD的值最小时,△DEF的周长最小,
当CD与CH重合时,CD的值最小,
∵?AB?CH=S,
∴CH=,
∴△DEF的周长的最小值为.
同课章节目录
