冀教版七年级上册:4.4整式的加减 课件(20张PPT)
文档属性
| 名称 | 冀教版七年级上册:4.4整式的加减 课件(20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-04 08:21:17 | ||
图片预览








文档简介
(共20张PPT)
2.合并同类项
(1)
(2)
(3)
(4)
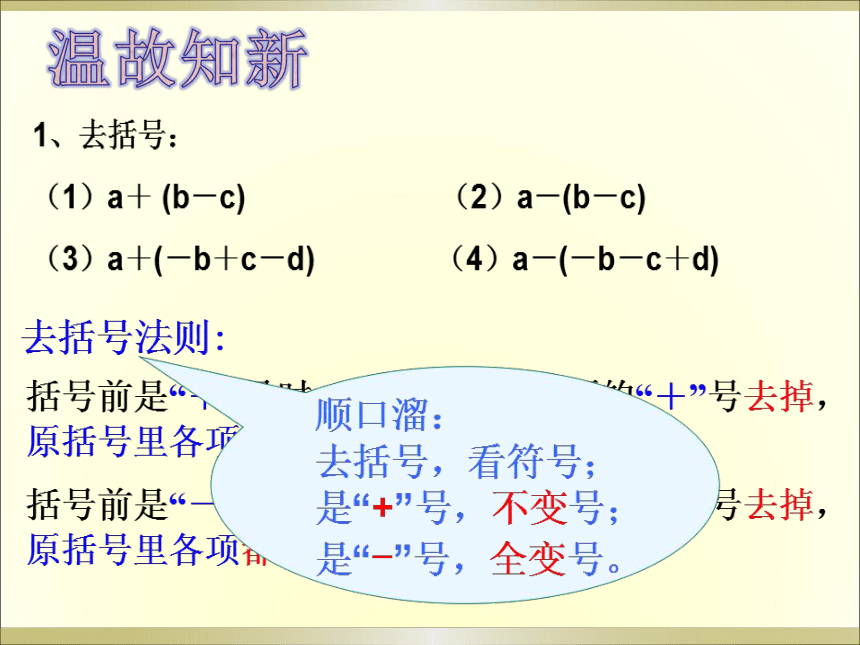
合并同类项法则:
在合并同类项时,把同类项的系数相加,字母和字母指数保持不变.
七年级(3)班分成三个小组,参加社会公益活动.
第一组有学生m名;第二组的人数比第一组的2倍少10人;
第三组的人数是第二组的一半. 请问:七年级(3)班共有学生多少名?
解:由题意得,
分析:第一组:m 名,
+
+
………列代数式
………去括号
………合并同类项
所以,七年级(3)班共有学生(4m-15)名。
( )
注:几个整式相加减,通常用括号把
每一个整式括起来,再用加减号连接。
……合并同类项
……列代数式
……去括号
去括号、合并同类项的化简过程,
( )
( )
-
它可以使结果变得简单.
解:由题意得,
[合作讨论]整式加减运算的一般步骤是怎样的?
……合并同类项
……列代数式
……去括号
( )
( )
-
写成加减算式(根据题意列代数式)
去括号
合并同类项
整式加减的结果仍然是( )
整式加减的一般步骤是:
(1)
(2)
(3)
题型一:直接的整式加减问题
例1.计算
解:
以算式形式直接给出
1.计算下列各题:
(1-2x+5x?)-(-3+3x-5x?)
4(x-1)-7(x+2)
(8xy-3y?)-5xy-2(3xy-2y?)
5m-3n-[-4m+(p+2n)]
解:
题型二:间接的整式加减问题
此类题目是以文字语言形式表述的数量关系,要先列出代数式再计算.
例2.求多项式 x2-7x-2 与 -2x2+4x-1 的差.
解:由题意得
(x2-7x-2)-(-2x2+4x-1)
= x2-7x-2+2x2-4x+1
= 3x2-11x-1
(去括号)
(合并同类项)
(根据题意列代数式)
例3. 教室里原有a名同学,后来有(b+2)名同学去打篮球,有(b+3)名同学去参加兴趣小组,问最后教室里还有多少名同学?
解:由题意得,
a-(b+2)-(b+3)
=a-b-2-b-3
=a-2b-5
(去括号)
(合并同类项)
(根据题意列代数式)
实际应用问题也要先列出代数式再计算。
答:最后教室里还有(a-2b-5 )名同学。
1.已知:A=x2+2y2-z2,B=x2-3y2-z2,
求:A-2B的值.
A-2B
=
= x2+2y2-z2-2x2+6y2+2z2
=-x2+8y2+z2
解:
(x2+2y2-z2)-2(x2-3y2-z2)
=(x2+2y2-z2)-(2x2-6y2-2z2)
2.一个多项式加上2x2-x3-5-3x4得
3x4-5x3-3,求这个多项式.
解:由题意得,
题型三:化简求值问题
解:
=15a2b-5ab2+4ab2-12a2b
=3a2b-ab2
当a=-2、b=3时,
原式 =3a2b-ab2
=36+18
=54
5(3a2b-ab2)-4(-ab2+3a2b)
=3×(-2)2×3-(-2)×32
=(15a2b-5ab2)-(-4ab2+12a2b)
=36-(-18)
2.先化简,再求值:
其中,
解:
你发现
了什么?
教学反思
1、通过这节课的学习你有什么收获?
2、你对本节课有什么疑问或建议?
1.已知A+B=3x2-5x+1,A-C=-2x+3x2-5,
当x=-2时,求B+C的值.
2.已知: s+t =21,3m-2n= -11,
求:(2s+9m)+[-(6n-2t)]的值.
1.已知A+B=3x2-5x+1,A-C=-2x+3x2-5,
当x = -2时,求B+C的值.
解: (2s+9m)+[-(6n-2t)]
=2s+9m+[-6n+2t ]
=2s+9m-6n+2t
=2(s+t)+3(3m-2n)
2.已知: s+t =21,3m-2n= -11,
求:(2s+9m)+[-(6n-2t)]的值.
当 s+t =21,3m-2n= -11时,
原式=2(s+t)+3(3m-2n)
=2×21+3×(-11)
=9
结束寄语
悟性的高低取决于有无悟“心”,
其实,人与人的差别就在于
你是否去思考,去发现?
2.合并同类项
(1)
(2)
(3)
(4)
合并同类项法则:
在合并同类项时,把同类项的系数相加,字母和字母指数保持不变.
七年级(3)班分成三个小组,参加社会公益活动.
第一组有学生m名;第二组的人数比第一组的2倍少10人;
第三组的人数是第二组的一半. 请问:七年级(3)班共有学生多少名?
解:由题意得,
分析:第一组:m 名,
+
+
………列代数式
………去括号
………合并同类项
所以,七年级(3)班共有学生(4m-15)名。
( )
注:几个整式相加减,通常用括号把
每一个整式括起来,再用加减号连接。
……合并同类项
……列代数式
……去括号
去括号、合并同类项的化简过程,
( )
( )
-
它可以使结果变得简单.
解:由题意得,
[合作讨论]整式加减运算的一般步骤是怎样的?
……合并同类项
……列代数式
……去括号
( )
( )
-
写成加减算式(根据题意列代数式)
去括号
合并同类项
整式加减的结果仍然是( )
整式加减的一般步骤是:
(1)
(2)
(3)
题型一:直接的整式加减问题
例1.计算
解:
以算式形式直接给出
1.计算下列各题:
(1-2x+5x?)-(-3+3x-5x?)
4(x-1)-7(x+2)
(8xy-3y?)-5xy-2(3xy-2y?)
5m-3n-[-4m+(p+2n)]
解:
题型二:间接的整式加减问题
此类题目是以文字语言形式表述的数量关系,要先列出代数式再计算.
例2.求多项式 x2-7x-2 与 -2x2+4x-1 的差.
解:由题意得
(x2-7x-2)-(-2x2+4x-1)
= x2-7x-2+2x2-4x+1
= 3x2-11x-1
(去括号)
(合并同类项)
(根据题意列代数式)
例3. 教室里原有a名同学,后来有(b+2)名同学去打篮球,有(b+3)名同学去参加兴趣小组,问最后教室里还有多少名同学?
解:由题意得,
a-(b+2)-(b+3)
=a-b-2-b-3
=a-2b-5
(去括号)
(合并同类项)
(根据题意列代数式)
实际应用问题也要先列出代数式再计算。
答:最后教室里还有(a-2b-5 )名同学。
1.已知:A=x2+2y2-z2,B=x2-3y2-z2,
求:A-2B的值.
A-2B
=
= x2+2y2-z2-2x2+6y2+2z2
=-x2+8y2+z2
解:
(x2+2y2-z2)-2(x2-3y2-z2)
=(x2+2y2-z2)-(2x2-6y2-2z2)
2.一个多项式加上2x2-x3-5-3x4得
3x4-5x3-3,求这个多项式.
解:由题意得,
题型三:化简求值问题
解:
=15a2b-5ab2+4ab2-12a2b
=3a2b-ab2
当a=-2、b=3时,
原式 =3a2b-ab2
=36+18
=54
5(3a2b-ab2)-4(-ab2+3a2b)
=3×(-2)2×3-(-2)×32
=(15a2b-5ab2)-(-4ab2+12a2b)
=36-(-18)
2.先化简,再求值:
其中,
解:
你发现
了什么?
教学反思
1、通过这节课的学习你有什么收获?
2、你对本节课有什么疑问或建议?
1.已知A+B=3x2-5x+1,A-C=-2x+3x2-5,
当x=-2时,求B+C的值.
2.已知: s+t =21,3m-2n= -11,
求:(2s+9m)+[-(6n-2t)]的值.
1.已知A+B=3x2-5x+1,A-C=-2x+3x2-5,
当x = -2时,求B+C的值.
解: (2s+9m)+[-(6n-2t)]
=2s+9m+[-6n+2t ]
=2s+9m-6n+2t
=2(s+t)+3(3m-2n)
2.已知: s+t =21,3m-2n= -11,
求:(2s+9m)+[-(6n-2t)]的值.
当 s+t =21,3m-2n= -11时,
原式=2(s+t)+3(3m-2n)
=2×21+3×(-11)
=9
结束寄语
悟性的高低取决于有无悟“心”,
其实,人与人的差别就在于
你是否去思考,去发现?
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
