人教版数学七年级上册:第三章 一元一次方程 3.4 实际问题与一元一次方程 第二课时 课件(24张PPT)
文档属性
| 名称 | 人教版数学七年级上册:第三章 一元一次方程 3.4 实际问题与一元一次方程 第二课时 课件(24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 688.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-03 10:43:06 | ||
图片预览








文档简介
(共24张PPT)
3.4 实际问题与一元一次方程
第二课时
(1)在小学里我们学过有关工程问题的应用题,这类应用题中一般有工作总量、工作时间、工作效率这三个量.这三个量间的关系是:
①工作总量=_______________________;
② 工作时间=_________________________;
③ 工作效率=_________________________;
人们常规定工程问题中的工作总量为____ .
(2)由以上公式可知:一件工作,甲用a小时完成,则甲的工作量可看成____,工作时间是_____小时,工作效率是_____. 若这件工作甲用6小时完成,则甲的工作效率是_____.
工作时间×工作效率
工作总量÷工作效率
工作总量÷工作时间
1
1
a
?
?
活动1
探究一:工程问题中的基本量
问题:整理一块地,由一个人做要80小时完成.
(1)一个人做1小时完成的工作量是_______;
(2)一个人做4小时完成的工作量是_______;
(3)一个人做x小时完成的工作量是________;
(4)工作效率相同的5个人做1小时完成的工作量是_______;
(5)工作效率相同的m个人做1小时完成的工作量是_______;
(6)工作效率相同的m个人做x小时完成的工作量是_________.
你能快速、准确地完成以上问题吗?
通过引例,回顾旧知
?
?
?
?
?
?
活动1
探究一:工程问题中的基本量
总结:
(1)在工程问题中,通常把全部工作量简单的表示为1.
(2)如果一件工作需要n小时完成,那么平均每小时完成的工作量就是 .
(3)工程问题中,当人均工作效率相同时:
工作量=人均效率×人数×工作时间 .
通过引例,回顾旧知
活动1
探究二:解决生活中工程问题
整理一批图书,由一个人做要40小时完成.现在计划由一部分人先做4小时,然后增加2人与他们一起做8小时,完成这项工作.假设这些人的工作效率相同,具体应先安排多少人工作?
“由一个人做要40小时完成”可以得到什么?
把总工作量设为1,则一个人1小时完成的工作量即人均效率为 .
大胆操作,探究新知
活动1
探究二:解决生活中工程问题
题目中哪些是已知量?哪些是未知的量?如果设先安排x人工作,则后来有________人一起工作;
已知量有:人均效率、总工作量、先后两个段的工作时间;未知量:前段时间安排的人数,如果设先安排x人工作,则后来有(x+2)人一起工作;
大胆操作,探究新知
这件工作是分哪两部分完成的?
一部分人先做4小时,然后增加2人一起再做8小时,完成这项工作.
活动2
探究二:解决生活中工程问题
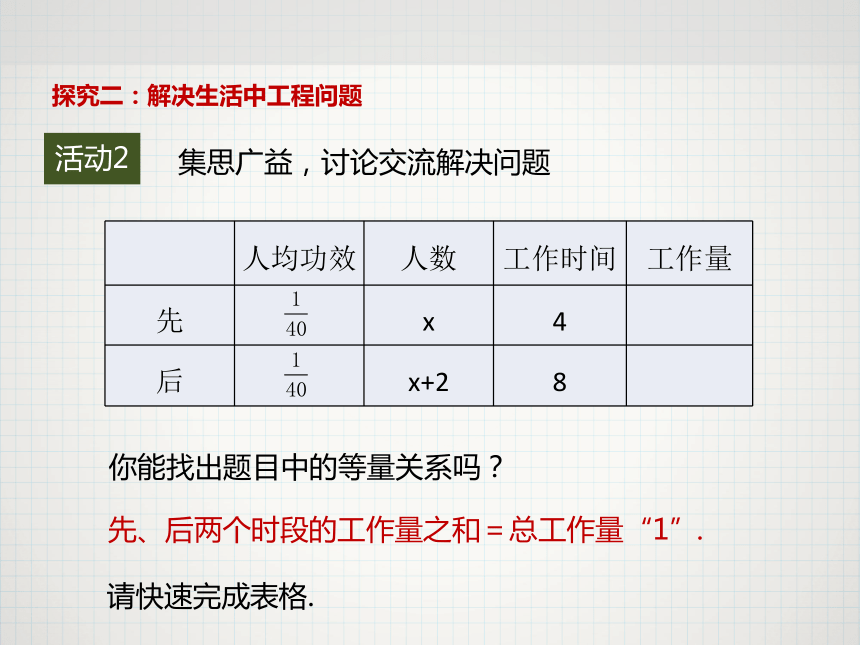
集思广益,讨论交流解决问题
你能找出题目中的等量关系吗?
先、后两个时段的工作量之和=总工作量“1”.
? 人均功效 人数 工作时间 工作量
先 x 4 ?
后 x+2 8 ?
请快速完成表格.
活动2
探究二:解决生活中工程问题
集思广益,讨论交流解决问题
你能根据相等关系列出方程吗?
解:设先安排x人先做4小时,则后来有(x+2)人一
起做了8小时;
由题意可得: ,
解得x=2;
答:应先安排2人先做4小时.
你能完整解答本题吗?
活动3
探究二:解决生活中工程问题
发散思维
变式1:整理一批图书,由一个人做要40小时完成.现在计划由一部分人先做4小时,然后增加2人与他们一起做8小时,完成这项工作的 .假设这些人的工作效率相同,具体应先安排多少人工作?
找出和活动①条件不同的地方,思考哪里发生了变化?该怎样解决这个问题?
活动3
探究二:解决生活中工程问题
发散思维
活动①中是“完成了整项工作”而本题是“只完成这项工作的 ”.
∴只需将总工作量1换成 即可.
∴方程变为: ,
解得:x=1,∴应先安排1人工作.
活动3
探究二:解决生活中工程问题
发散思维
变式2:整理一批图书,由一个人做要40小时完成.现在计划由一部分人先做4小时,然后增加2人与他们一起做8小时,最后再由增加的2人做6小时,完成这项工作. 假设这些人的工作效率相同,具体应先安排多少人工作?
找出和活动①条件不同的地方,思考哪里发生了变化?该怎样解决这个问题?
活动3
探究二:解决生活中工程问题
发散思维
与活动①相比,多出了一段时间,即最后再由增加的2人做6小时,才完成这项工作.
∴先、后两个时段的工作量之和+增加的2人做6小时的工作量=总工作量“1”
∴方程变为: ,解得:x=1,
∴应先安排1人工作.
总结:通过设置“完成的工作量”的改变,进一步感受“完成的总工作量=各部分工作量之和”.明确工程问题的关键所在,认真读题找到有效的等量关系是解决实际问题的关键所在。
活动4
探究二:解决生活中工程问题
反思过程,发现规律
有关工程问题的应用题中:
(1)通常把全部工作量简单表示为1.
(2)计算工作量的基本公式是:工作量=人均效率×人数×时间,它能对加入“人数”以后的工程问题更好的求解.
(3)用一元一次方程解决实际问题的基本过程:
活动1
探究三:运用知识解决问题
通过前面的探究,我们知道了利用一元一次方程解决实际问题的基本过程,利用这些步骤和方法可以解决一些怎样的工程问题呢?
例1 某项工作,甲单独做需要4小时,乙单独做需要6小时,甲先做30分钟,然后甲乙合作,问:甲乙合作还需要多少小时才能完成全部工作?
活动1
探究三:运用知识解决问题
【解题过程】解:设甲乙合作还需要x小时才能完成全部工作,根据题意得:
或 ,解得:x=2.1 .
答:甲乙合作还需要2.1小时才能完成全部工作.
【思路点拨】
抓工程问题中的基本量:工作量=工作时间×工作效率.
从题中找出等量关系:甲工作量+乙工作量=总工作量1,注意要化单位.
活动1
探究三:运用知识解决问题
练习:一条地下管线由甲工程队单独铺设需要12天,由乙工程队单独铺设需要24天,如果由这两个工程队从两端同时施工,要多少天可以铺设好这条管线?
【解题过程】
解:设要x天可以铺设好这条管线,根据题意得:
解得:x=8 .
答:要8天可以铺设好这条管线.
活动1
探究三:运用知识解决问题
练习:一条地下管线由甲工程队单独铺设需要12天,由乙工程队单独铺设需要24天,如果由这两个工程队从两端同时施工,要多少天可以铺设好这条管线?
【解题过程】
解:设要x天可以铺设好这条管线,根据题意得:
,解得:x=8 .
答:要8天可以铺设好这条管线.
【思路点拨】把总工作量看作1. 抓等量关系:
甲工作量+乙工作量=总工作量1
活动2
探究三:运用知识解决问题
例2 一水池,单开进水管3小时可将水池注满,单开出水管4小时可将满池水放完,现对空水池先打开进水管2小时,然后打开出水管,使进水管、出水管一起开放,问再过几小时可将水池注满?
【解题过程】
解:设经再过x小时可以将水池注满,根据题意得:
,解得:x=4
答:再过4小时可将水池注满.
【思路点拨】注意进水管和出水管同时打开,要将水池注满,则需抓等量关系:“进水管的进水量—出水管的出水量”=1.
活动2
探究三:运用知识解决问题
练习:一件工作,由2个人做要6个月完成,现计划由一部分人先做 1个月,然后再增加4个人和他们一起做1个月,完成这件工作的 ,假设这些人的工作效率相同,问:应先安排多少人工作?
【解题过程】
解:设应先安排x个人工作,
根据题意得: ,解得:x=3 .
答:应先安排3个人工作.
【思路点拨】 本题先要求出的是每个人的人均工作效率 ,然后再根据“先做的工作量+后做的工作量= ”这一等量关系列方程.
活动3
探究三:运用知识解决问题
例3 有一份文件需要录入电脑,由甲单独录入需12小时可以完成,由乙单独录入需8小时可以完成.
(1)这份文件由甲、乙两个共同录入,则需要多少小时完成?
(2)这份文件由甲、乙两个共同录入,如果中间乙休息1小时,那么录完这份文件共需多少小时?
(3)如果这份文件由甲乙轮流打字,每轮中甲先录1小时,再由乙录1小时,那么录完这份文件需要多少小时?
【思路点拨】
弄清每一问中这项工作是怎么完成的?抓等量关系:总工作量=各阶段工作量的和 .
活动3
探究三:运用知识解决问题
【解题过程】
解:(1)设需x小时才能完成, 根据题意,列方程得: ,
解得:x=4.8 . 答:需4.8小时才能完成.
(2)需y小时才能完成,根据题意,列方程得: ,
解得:y=5.4 . 答:需5.4小时才能完成.
(3)甲乙每一轮打完这份文件的 ,因为 ,所以打完这份文件需4轮以上,但不到5轮.
打4轮以后还剩下的打字任务为: ,甲打一小时的工效为 ,故甲打字一小时后剩下的任务为 ,所以乙还需 小时,因此完成任务共需 小时.
活动3
探究三:运用知识解决问题
练习:安装某小区的自来水管,甲单独完成需要14天,乙单独完成需要18天,丙单独完成需要12天,前7天由甲、乙两人合作,但乙中途离开一段时间,后2天由乙、丙合作完成任务,问乙中途离开了几天?
【解题过程】 解:设乙中途离开了x天,根据题意,列方程得: .解得: x=3 . 答:乙中途离开了3天.
【思路点拨】把总工作量看作1. 抓等量关系:甲工作量+乙工作量+丙工作量=总工作量1,关键是表示乙的工作时间.
(1)列一元一次方程解决实际问题的一般步骤:
审、设、列、解、检、答.
(2)在工程问题中,通常把全部工作量简单的表示为1.
(3)如果一件工作需要n小时完成,那么平均每小时完成的工作量就是 .
(4)工程问题中,当人均工作效率相同时:
工作量=人均效率×人数×工作时间
(1)工作量= 工作效率×工作时间;
(2)总工作量=各阶段工作量的和;
(3)工作量= 人均效率×人数×时间.
3.4 实际问题与一元一次方程
第二课时
(1)在小学里我们学过有关工程问题的应用题,这类应用题中一般有工作总量、工作时间、工作效率这三个量.这三个量间的关系是:
①工作总量=_______________________;
② 工作时间=_________________________;
③ 工作效率=_________________________;
人们常规定工程问题中的工作总量为____ .
(2)由以上公式可知:一件工作,甲用a小时完成,则甲的工作量可看成____,工作时间是_____小时,工作效率是_____. 若这件工作甲用6小时完成,则甲的工作效率是_____.
工作时间×工作效率
工作总量÷工作效率
工作总量÷工作时间
1
1
a
?
?
活动1
探究一:工程问题中的基本量
问题:整理一块地,由一个人做要80小时完成.
(1)一个人做1小时完成的工作量是_______;
(2)一个人做4小时完成的工作量是_______;
(3)一个人做x小时完成的工作量是________;
(4)工作效率相同的5个人做1小时完成的工作量是_______;
(5)工作效率相同的m个人做1小时完成的工作量是_______;
(6)工作效率相同的m个人做x小时完成的工作量是_________.
你能快速、准确地完成以上问题吗?
通过引例,回顾旧知
?
?
?
?
?
?
活动1
探究一:工程问题中的基本量
总结:
(1)在工程问题中,通常把全部工作量简单的表示为1.
(2)如果一件工作需要n小时完成,那么平均每小时完成的工作量就是 .
(3)工程问题中,当人均工作效率相同时:
工作量=人均效率×人数×工作时间 .
通过引例,回顾旧知
活动1
探究二:解决生活中工程问题
整理一批图书,由一个人做要40小时完成.现在计划由一部分人先做4小时,然后增加2人与他们一起做8小时,完成这项工作.假设这些人的工作效率相同,具体应先安排多少人工作?
“由一个人做要40小时完成”可以得到什么?
把总工作量设为1,则一个人1小时完成的工作量即人均效率为 .
大胆操作,探究新知
活动1
探究二:解决生活中工程问题
题目中哪些是已知量?哪些是未知的量?如果设先安排x人工作,则后来有________人一起工作;
已知量有:人均效率、总工作量、先后两个段的工作时间;未知量:前段时间安排的人数,如果设先安排x人工作,则后来有(x+2)人一起工作;
大胆操作,探究新知
这件工作是分哪两部分完成的?
一部分人先做4小时,然后增加2人一起再做8小时,完成这项工作.
活动2
探究二:解决生活中工程问题
集思广益,讨论交流解决问题
你能找出题目中的等量关系吗?
先、后两个时段的工作量之和=总工作量“1”.
? 人均功效 人数 工作时间 工作量
先 x 4 ?
后 x+2 8 ?
请快速完成表格.
活动2
探究二:解决生活中工程问题
集思广益,讨论交流解决问题
你能根据相等关系列出方程吗?
解:设先安排x人先做4小时,则后来有(x+2)人一
起做了8小时;
由题意可得: ,
解得x=2;
答:应先安排2人先做4小时.
你能完整解答本题吗?
活动3
探究二:解决生活中工程问题
发散思维
变式1:整理一批图书,由一个人做要40小时完成.现在计划由一部分人先做4小时,然后增加2人与他们一起做8小时,完成这项工作的 .假设这些人的工作效率相同,具体应先安排多少人工作?
找出和活动①条件不同的地方,思考哪里发生了变化?该怎样解决这个问题?
活动3
探究二:解决生活中工程问题
发散思维
活动①中是“完成了整项工作”而本题是“只完成这项工作的 ”.
∴只需将总工作量1换成 即可.
∴方程变为: ,
解得:x=1,∴应先安排1人工作.
活动3
探究二:解决生活中工程问题
发散思维
变式2:整理一批图书,由一个人做要40小时完成.现在计划由一部分人先做4小时,然后增加2人与他们一起做8小时,最后再由增加的2人做6小时,完成这项工作. 假设这些人的工作效率相同,具体应先安排多少人工作?
找出和活动①条件不同的地方,思考哪里发生了变化?该怎样解决这个问题?
活动3
探究二:解决生活中工程问题
发散思维
与活动①相比,多出了一段时间,即最后再由增加的2人做6小时,才完成这项工作.
∴先、后两个时段的工作量之和+增加的2人做6小时的工作量=总工作量“1”
∴方程变为: ,解得:x=1,
∴应先安排1人工作.
总结:通过设置“完成的工作量”的改变,进一步感受“完成的总工作量=各部分工作量之和”.明确工程问题的关键所在,认真读题找到有效的等量关系是解决实际问题的关键所在。
活动4
探究二:解决生活中工程问题
反思过程,发现规律
有关工程问题的应用题中:
(1)通常把全部工作量简单表示为1.
(2)计算工作量的基本公式是:工作量=人均效率×人数×时间,它能对加入“人数”以后的工程问题更好的求解.
(3)用一元一次方程解决实际问题的基本过程:
活动1
探究三:运用知识解决问题
通过前面的探究,我们知道了利用一元一次方程解决实际问题的基本过程,利用这些步骤和方法可以解决一些怎样的工程问题呢?
例1 某项工作,甲单独做需要4小时,乙单独做需要6小时,甲先做30分钟,然后甲乙合作,问:甲乙合作还需要多少小时才能完成全部工作?
活动1
探究三:运用知识解决问题
【解题过程】解:设甲乙合作还需要x小时才能完成全部工作,根据题意得:
或 ,解得:x=2.1 .
答:甲乙合作还需要2.1小时才能完成全部工作.
【思路点拨】
抓工程问题中的基本量:工作量=工作时间×工作效率.
从题中找出等量关系:甲工作量+乙工作量=总工作量1,注意要化单位.
活动1
探究三:运用知识解决问题
练习:一条地下管线由甲工程队单独铺设需要12天,由乙工程队单独铺设需要24天,如果由这两个工程队从两端同时施工,要多少天可以铺设好这条管线?
【解题过程】
解:设要x天可以铺设好这条管线,根据题意得:
解得:x=8 .
答:要8天可以铺设好这条管线.
活动1
探究三:运用知识解决问题
练习:一条地下管线由甲工程队单独铺设需要12天,由乙工程队单独铺设需要24天,如果由这两个工程队从两端同时施工,要多少天可以铺设好这条管线?
【解题过程】
解:设要x天可以铺设好这条管线,根据题意得:
,解得:x=8 .
答:要8天可以铺设好这条管线.
【思路点拨】把总工作量看作1. 抓等量关系:
甲工作量+乙工作量=总工作量1
活动2
探究三:运用知识解决问题
例2 一水池,单开进水管3小时可将水池注满,单开出水管4小时可将满池水放完,现对空水池先打开进水管2小时,然后打开出水管,使进水管、出水管一起开放,问再过几小时可将水池注满?
【解题过程】
解:设经再过x小时可以将水池注满,根据题意得:
,解得:x=4
答:再过4小时可将水池注满.
【思路点拨】注意进水管和出水管同时打开,要将水池注满,则需抓等量关系:“进水管的进水量—出水管的出水量”=1.
活动2
探究三:运用知识解决问题
练习:一件工作,由2个人做要6个月完成,现计划由一部分人先做 1个月,然后再增加4个人和他们一起做1个月,完成这件工作的 ,假设这些人的工作效率相同,问:应先安排多少人工作?
【解题过程】
解:设应先安排x个人工作,
根据题意得: ,解得:x=3 .
答:应先安排3个人工作.
【思路点拨】 本题先要求出的是每个人的人均工作效率 ,然后再根据“先做的工作量+后做的工作量= ”这一等量关系列方程.
活动3
探究三:运用知识解决问题
例3 有一份文件需要录入电脑,由甲单独录入需12小时可以完成,由乙单独录入需8小时可以完成.
(1)这份文件由甲、乙两个共同录入,则需要多少小时完成?
(2)这份文件由甲、乙两个共同录入,如果中间乙休息1小时,那么录完这份文件共需多少小时?
(3)如果这份文件由甲乙轮流打字,每轮中甲先录1小时,再由乙录1小时,那么录完这份文件需要多少小时?
【思路点拨】
弄清每一问中这项工作是怎么完成的?抓等量关系:总工作量=各阶段工作量的和 .
活动3
探究三:运用知识解决问题
【解题过程】
解:(1)设需x小时才能完成, 根据题意,列方程得: ,
解得:x=4.8 . 答:需4.8小时才能完成.
(2)需y小时才能完成,根据题意,列方程得: ,
解得:y=5.4 . 答:需5.4小时才能完成.
(3)甲乙每一轮打完这份文件的 ,因为 ,所以打完这份文件需4轮以上,但不到5轮.
打4轮以后还剩下的打字任务为: ,甲打一小时的工效为 ,故甲打字一小时后剩下的任务为 ,所以乙还需 小时,因此完成任务共需 小时.
活动3
探究三:运用知识解决问题
练习:安装某小区的自来水管,甲单独完成需要14天,乙单独完成需要18天,丙单独完成需要12天,前7天由甲、乙两人合作,但乙中途离开一段时间,后2天由乙、丙合作完成任务,问乙中途离开了几天?
【解题过程】 解:设乙中途离开了x天,根据题意,列方程得: .解得: x=3 . 答:乙中途离开了3天.
【思路点拨】把总工作量看作1. 抓等量关系:甲工作量+乙工作量+丙工作量=总工作量1,关键是表示乙的工作时间.
(1)列一元一次方程解决实际问题的一般步骤:
审、设、列、解、检、答.
(2)在工程问题中,通常把全部工作量简单的表示为1.
(3)如果一件工作需要n小时完成,那么平均每小时完成的工作量就是 .
(4)工程问题中,当人均工作效率相同时:
工作量=人均效率×人数×工作时间
(1)工作量= 工作效率×工作时间;
(2)总工作量=各阶段工作量的和;
(3)工作量= 人均效率×人数×时间.
