6.1.2 平方根 课件
图片预览






文档简介
(共19张PPT)
人教版 初中数学
第五章 相交线与平行线
6.1.2 平方根
复习引入
什么叫做算术平方根?
一般地,如果一个正数x的平方等于a ,即x2=a ,那么这个正数x叫做a的算术平方根。
a的算术平方根记为:____ 读作: ________
a叫做:_________
根号a
被开方数
正数的算术平方根是正数,0的算术平方根是0,负数没有算术平方根。
探究新知
由于 ,
所以这个数是4或-4.
思考
4是16的算术平方根,
-4与16的算术平方根有什么关系?
如果一个数的平方等于16,这个数是多少?
互为相反数
探究新知
根据上面的研究过程填表:
如果我们把 分别叫做
的平方根,你能类比算术平方根的说法,说出什么是平方根吗?
类比
探究新知
一般地,如果一个数的平方等于a,那么这个数叫
做a的平方根或二次方根.这就是说,如果 ,
那么x 叫做a的平方根。
例如:5和-5是25的平方根,
简记为±5是25的平方根。
定义
±5表示+5和-5两个数。
探究新知
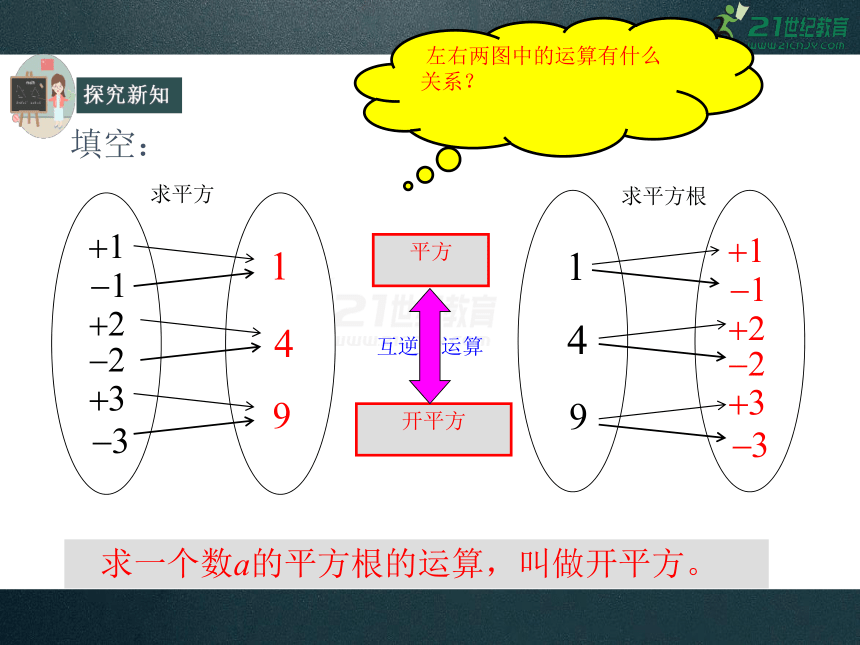
填空:
求平方
求平方根
左右两图中的运算有什么关系?
平方
开平方
互逆 运算
求一个数a的平方根的运算,叫做开平方。
练一练
例1 求下列各数的平方根:
解:(1)因为(±10)2=100,
所以100的平方根是±10,
即
(1) (2) (3) (4) (5)
练一练
例1 求下列各数的平方根:
(1) (2) (3) (4) (5)
解:(2)因为 ,
所以 的平方根是 ,
即 。
练一练
例1 求下列各数的平方根:
(1) (2) (3) (4) (5)
解:(3)因为(±0.5)2=0.25,
所以0.25的平方根是±0.5,
即 。
练一练
例1 求下列各数的平方根:
(1) (2) (3) (4) (5)
解:(4)因为 ,
所以 的平方根是 ,
即 。
练一练
例1 求下列各数的平方根:
(1) (2) (3) (4) (5)
解:(5)因为02=0,
所以0的平方根是0,
即 。
探究新知
正数的平方根有两个,它们互为相反数;
0的平方根就是0 ;
负数没有平方根。
2、0的平方根是多少?
3、负数有平方根吗?
思 考
1、正数的平方根有什么特点?
探究新知
正数的平方根如何表示呢?
正数a的平方根记为 读作: 正、负根号a
表示正数a的算术平方根
表示正数a的负的平方根
练一练
解:(1) ;
(2) ;
(3) 。
说出下列各式的意义,并求它们的值:
如果知道一个数的算术平方根就可以立即写出它的负的平方根,为什么?
(1) (2) (3)
随堂训练
1、下列各式正确的是( ).
A. B.
C. D.
D
2、判断下列说法是否正确。
(1)64的平方根是8;
(2)4是16的平方根;
(3)-6是36的平方根;
(4)81的平方根是 。
×
√
√
√
随堂训练
3、计算下列各式的值:
解:(1) ;
(2) ;
(3) 。
拓展延伸
已知 ,则 的值为多少?
解:∵
∴a+3=0, b2-2b-6=0
解得,a=-3,b2-2b=6,
可得2b2-4b=12,
则2b2-4b-a=12-(-3)=15
课堂小结
今天我们学习了哪些知识?
1、能总结平方根与算术平方根的概念的联系与区别吗?
2、平方根的性质是什么?
https://www.21cnjy.com/help/help_extract.php
人教版 初中数学
第五章 相交线与平行线
6.1.2 平方根
复习引入
什么叫做算术平方根?
一般地,如果一个正数x的平方等于a ,即x2=a ,那么这个正数x叫做a的算术平方根。
a的算术平方根记为:____ 读作: ________
a叫做:_________
根号a
被开方数
正数的算术平方根是正数,0的算术平方根是0,负数没有算术平方根。
探究新知
由于 ,
所以这个数是4或-4.
思考
4是16的算术平方根,
-4与16的算术平方根有什么关系?
如果一个数的平方等于16,这个数是多少?
互为相反数
探究新知
根据上面的研究过程填表:
如果我们把 分别叫做
的平方根,你能类比算术平方根的说法,说出什么是平方根吗?
类比
探究新知
一般地,如果一个数的平方等于a,那么这个数叫
做a的平方根或二次方根.这就是说,如果 ,
那么x 叫做a的平方根。
例如:5和-5是25的平方根,
简记为±5是25的平方根。
定义
±5表示+5和-5两个数。
探究新知
填空:
求平方
求平方根
左右两图中的运算有什么关系?
平方
开平方
互逆 运算
求一个数a的平方根的运算,叫做开平方。
练一练
例1 求下列各数的平方根:
解:(1)因为(±10)2=100,
所以100的平方根是±10,
即
(1) (2) (3) (4) (5)
练一练
例1 求下列各数的平方根:
(1) (2) (3) (4) (5)
解:(2)因为 ,
所以 的平方根是 ,
即 。
练一练
例1 求下列各数的平方根:
(1) (2) (3) (4) (5)
解:(3)因为(±0.5)2=0.25,
所以0.25的平方根是±0.5,
即 。
练一练
例1 求下列各数的平方根:
(1) (2) (3) (4) (5)
解:(4)因为 ,
所以 的平方根是 ,
即 。
练一练
例1 求下列各数的平方根:
(1) (2) (3) (4) (5)
解:(5)因为02=0,
所以0的平方根是0,
即 。
探究新知
正数的平方根有两个,它们互为相反数;
0的平方根就是0 ;
负数没有平方根。
2、0的平方根是多少?
3、负数有平方根吗?
思 考
1、正数的平方根有什么特点?
探究新知
正数的平方根如何表示呢?
正数a的平方根记为 读作: 正、负根号a
表示正数a的算术平方根
表示正数a的负的平方根
练一练
解:(1) ;
(2) ;
(3) 。
说出下列各式的意义,并求它们的值:
如果知道一个数的算术平方根就可以立即写出它的负的平方根,为什么?
(1) (2) (3)
随堂训练
1、下列各式正确的是( ).
A. B.
C. D.
D
2、判断下列说法是否正确。
(1)64的平方根是8;
(2)4是16的平方根;
(3)-6是36的平方根;
(4)81的平方根是 。
×
√
√
√
随堂训练
3、计算下列各式的值:
解:(1) ;
(2) ;
(3) 。
拓展延伸
已知 ,则 的值为多少?
解:∵
∴a+3=0, b2-2b-6=0
解得,a=-3,b2-2b=6,
可得2b2-4b=12,
则2b2-4b-a=12-(-3)=15
课堂小结
今天我们学习了哪些知识?
1、能总结平方根与算术平方根的概念的联系与区别吗?
2、平方根的性质是什么?
https://www.21cnjy.com/help/help_extract.php
