2.11有理数的混合运算课件(共16张PPT)
文档属性
| 名称 | 2.11有理数的混合运算课件(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 562.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-05 23:09:04 | ||
图片预览





文档简介
(共16张PPT)
2.11 有理数的混合运算 (第一课时)
信宜市合水中学
黄坤
学习目标
1.掌握有理数混合运算的法则,并能熟练地进行有理数加、减、乘、除、乘方的混合运算.(重点)
2.在运算过程中能合理地使用运算律简化运算.(难点)
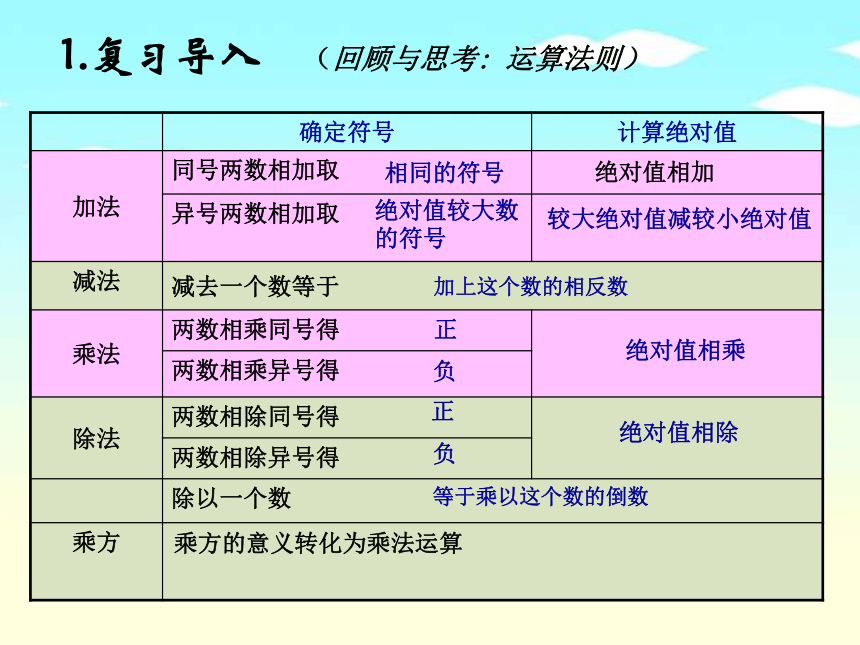
确定符号 计算绝对值
加法 同号两数相加取
异号两数相加取
减法 减去一个数等于
乘法 两数相乘同号得
两数相乘异号得
除法 两数相除同号得
两数相除异号得
除以一个数
乘方
1.复习导入 (回顾与思考: 运算法则)
相同的符号
绝对值相加
较大绝对值减较小绝对值
加上这个数的相反数
正
负
绝对值相乘
正
负
绝对值相除
等于乘以这个数的倒数
乘方的意义转化为乘法运算
绝对值较大数
的符号
1.复习导入 (快速计算)
(1)(-3)+(-2)= (2)(-6)-(-8)=
(3)(+6)×(+3)=
(4)(-18)÷(-9)=
(5)
=
-5
2
18
2
27
思考:我们学习过的运算类型有哪些呢?
加,减是同级运算
乘,除是同级运算
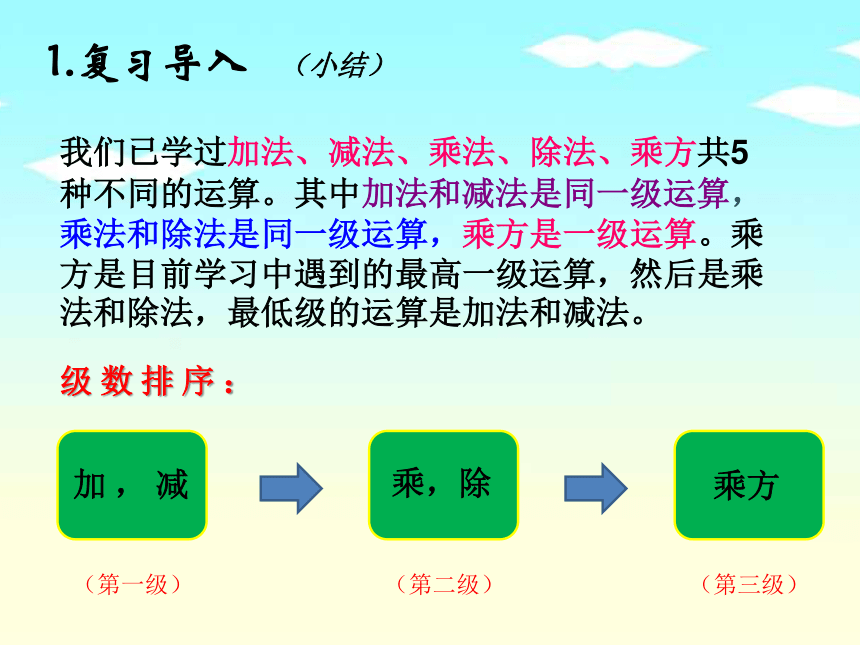
1.复习导入 (小结)
我们已学过加法、减法、乘法、除法、乘方共5种不同的运算。其中加法和减法是同一级运算,乘法和除法是同一级运算,乘方是一级运算。乘方是目前学习中遇到的最高一级运算,然后是乘法和除法,最低级的运算是加法和减法。
乘方
加 , 减
乘,除
(第一级)
(第三级)
(第二级)
级数排序:
2.探索新知
不同级混合运算(例题讲解)
18 - 6 ÷(-2) ×(-)
乘,除(第二级)
加,减(第一级)
解:原式=18 -(-3)×(-)
=18 - 1
= 17
2.探索新知
不同级混合运算(例题讲解)
加,减(第一级)
乘,除(第二级)
乘方(第三级)
解:原式=16 ÷(-8)-(-) ×(-4)
=(-2)-
=-2
先算乘方(第三级)
再算乘除(第二级)
最后算加减(第一级)
2.探索新知
(归纳小结1)
有理数混合运算的法则:
(1)先算乘方,再算乘除,最后算加减;
(2)如有括号,先进行括号里的运算.
先算括号里的
乘方
第三级
加减
第一级
乘除
第二级
2.探索新知
同级,不同级混合运算(练一练)
(1)3×(-4)+(-28)÷7 (2)(-3)×(-4)÷2
(3)4× + 6 (4)
(1)解:原式=(-12)+(-4)
=-16
(2)解:原式=12÷2
=6
(3)解:原式= 4×(-8)+6
=(-32)+6
= - 26
(4)解:原式= 9×
= -11
2.探索新知
(一题多解)
解法一:
解法二:
点拨:在运算过程中,巧用运算律,可简化计算
讨论交流:你认为哪种方法更好呢?
(4)
2.探索新知
(归纳小结2)
加法交换律:a+b=b+a;
加法结合律:(a+b)+c=a+(b+c);
乘法交换律:axb=bxa;
乘法结合律:(axb)xc=ax(bxc);
乘法分配律:ax(b+c)=axb+axc.
解:原式=(-60)× +(-60)×
=(-45)+(-50)
=- 95
3.课堂小测
1.判断下列各式是否成立,成立的打√,不成立的打×
(1)-3+4×2+1=1×3 ( )
(2)-20÷(-4)×(-5)=-20÷20 ( )
(3) ( )
(4) ( )
2.计算下列各题
(1) (2)
×
×
√
√
4.课堂小结
有理数混合运算的法则:
(1)先算乘方,再算乘除,最后算加减;
(2)如有括号,先进行括号里的运算.
加法交换律:a+b=b+a;
加法结合律:(a+b)+c=a+(b+c);
乘法交换律:axb=bxa;
乘法结合律:(axb)xc=ax(bxc);
乘法分配律:ax(b+c)=axb+axc.
5.布置作业
课本:67页 第一题(1)--(6)
你会玩“24点”游戏吗?
从一副扑克牌(去掉大小王)中任意抽取4张,根据牌面上的数字进行混合运算(每张牌只能用一次),使得运算结果为24或-24。其中红色扑克牌代表负数,黑色扑克牌代表正数,J、Q、K分别表示11、12、13。
(1)小飞抽到了
他运用下面的方法凑成了24:
数学游戏
1
-8
-7
3
(2)请将下面的每组扑克牌凑成24。
12×3-(-12)×(-1)=36-12=24
2.11 有理数的混合运算 (第一课时)
信宜市合水中学
黄坤
学习目标
1.掌握有理数混合运算的法则,并能熟练地进行有理数加、减、乘、除、乘方的混合运算.(重点)
2.在运算过程中能合理地使用运算律简化运算.(难点)
确定符号 计算绝对值
加法 同号两数相加取
异号两数相加取
减法 减去一个数等于
乘法 两数相乘同号得
两数相乘异号得
除法 两数相除同号得
两数相除异号得
除以一个数
乘方
1.复习导入 (回顾与思考: 运算法则)
相同的符号
绝对值相加
较大绝对值减较小绝对值
加上这个数的相反数
正
负
绝对值相乘
正
负
绝对值相除
等于乘以这个数的倒数
乘方的意义转化为乘法运算
绝对值较大数
的符号
1.复习导入 (快速计算)
(1)(-3)+(-2)= (2)(-6)-(-8)=
(3)(+6)×(+3)=
(4)(-18)÷(-9)=
(5)
=
-5
2
18
2
27
思考:我们学习过的运算类型有哪些呢?
加,减是同级运算
乘,除是同级运算
1.复习导入 (小结)
我们已学过加法、减法、乘法、除法、乘方共5种不同的运算。其中加法和减法是同一级运算,乘法和除法是同一级运算,乘方是一级运算。乘方是目前学习中遇到的最高一级运算,然后是乘法和除法,最低级的运算是加法和减法。
乘方
加 , 减
乘,除
(第一级)
(第三级)
(第二级)
级数排序:
2.探索新知
不同级混合运算(例题讲解)
18 - 6 ÷(-2) ×(-)
乘,除(第二级)
加,减(第一级)
解:原式=18 -(-3)×(-)
=18 - 1
= 17
2.探索新知
不同级混合运算(例题讲解)
加,减(第一级)
乘,除(第二级)
乘方(第三级)
解:原式=16 ÷(-8)-(-) ×(-4)
=(-2)-
=-2
先算乘方(第三级)
再算乘除(第二级)
最后算加减(第一级)
2.探索新知
(归纳小结1)
有理数混合运算的法则:
(1)先算乘方,再算乘除,最后算加减;
(2)如有括号,先进行括号里的运算.
先算括号里的
乘方
第三级
加减
第一级
乘除
第二级
2.探索新知
同级,不同级混合运算(练一练)
(1)3×(-4)+(-28)÷7 (2)(-3)×(-4)÷2
(3)4× + 6 (4)
(1)解:原式=(-12)+(-4)
=-16
(2)解:原式=12÷2
=6
(3)解:原式= 4×(-8)+6
=(-32)+6
= - 26
(4)解:原式= 9×
= -11
2.探索新知
(一题多解)
解法一:
解法二:
点拨:在运算过程中,巧用运算律,可简化计算
讨论交流:你认为哪种方法更好呢?
(4)
2.探索新知
(归纳小结2)
加法交换律:a+b=b+a;
加法结合律:(a+b)+c=a+(b+c);
乘法交换律:axb=bxa;
乘法结合律:(axb)xc=ax(bxc);
乘法分配律:ax(b+c)=axb+axc.
解:原式=(-60)× +(-60)×
=(-45)+(-50)
=- 95
3.课堂小测
1.判断下列各式是否成立,成立的打√,不成立的打×
(1)-3+4×2+1=1×3 ( )
(2)-20÷(-4)×(-5)=-20÷20 ( )
(3) ( )
(4) ( )
2.计算下列各题
(1) (2)
×
×
√
√
4.课堂小结
有理数混合运算的法则:
(1)先算乘方,再算乘除,最后算加减;
(2)如有括号,先进行括号里的运算.
加法交换律:a+b=b+a;
加法结合律:(a+b)+c=a+(b+c);
乘法交换律:axb=bxa;
乘法结合律:(axb)xc=ax(bxc);
乘法分配律:ax(b+c)=axb+axc.
5.布置作业
课本:67页 第一题(1)--(6)
你会玩“24点”游戏吗?
从一副扑克牌(去掉大小王)中任意抽取4张,根据牌面上的数字进行混合运算(每张牌只能用一次),使得运算结果为24或-24。其中红色扑克牌代表负数,黑色扑克牌代表正数,J、Q、K分别表示11、12、13。
(1)小飞抽到了
他运用下面的方法凑成了24:
数学游戏
1
-8
-7
3
(2)请将下面的每组扑克牌凑成24。
12×3-(-12)×(-1)=36-12=24
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
