1.1.3 导数的几何意义 课件(32张PPT)
文档属性
| 名称 | 1.1.3 导数的几何意义 课件(32张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-10 09:28:25 | ||
图片预览










文档简介
课件32张PPT。1.1.3 导数的几何意义
1.了解导函数的概念;理解导数的几何意义.
2.会求导函数.
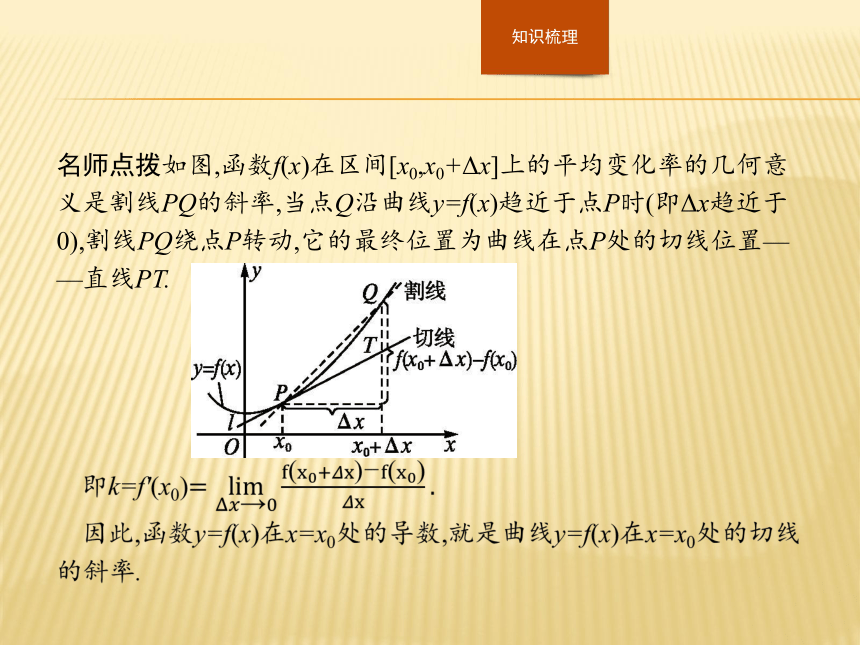
3.根据导数的几何意义,会求曲线上某点处的切线方程.??名师点拨如图,函数f(x)在区间[x0,x0+Δx]上的平均变化率的几何意义是割线PQ的斜率,当点Q沿曲线y=f(x)趋近于点P时(即Δx趋近于0),割线PQ绕点P转动,它的最终位置为曲线在点P处的切线位置——直线PT.?【做一做1-1】 若f'(x0)=0,则曲线y=f(x)在点(x0,f(x0))处的切线( )
A.不存在
B.与x轴平行或重合
C.与x轴垂直
D.与x轴斜交
解析:由导数的几何意义知,曲线y=f(x)在点(x0,f(x0))处的切线斜率为0,故选B.
答案:B??【做一做2-2】 若曲线f(x)的导函数为f'(x)=2x+3,则f'(3)等于( )
A.0 B.2 C.3 D.9
答案:D【做一做2-1】 函数在某一点处的导数是( )
A.在该点的函数值的改变量与自变量的改变量的比
B.一个函数
C.一个常数,不是变数
D.函数在这一点与它附近一点之间的平均变化率
解析:根据函数在一点处的导数的定义,可知选C.
答案:C?2.“用割线的极限位置来定义切线”和“与曲线只有一个公共点的直线是切线”的区别是什么?
剖析:在初中我们学习过圆的切线:当直线和圆有唯一公共点时,我们称直线和圆相切,这时直线叫做圆的切线,唯一的公共点叫做切点,圆是一种特殊的曲线.如果将圆的切线推广为一般曲线的切线:当直线和曲线有唯一公共点时,直线叫做曲线过该点的切线,这种推广是不妥当的.观察图中的曲线C,直线l1虽然与曲线C有唯一的公共点M,但我们不能说直线l1与曲线C相切;而直线l2尽管与曲线C有不止一个公共点,我们还是说直线l2是曲线C在点N处的切线.因此,对于一般的曲线,必须重新寻求曲线切线的定义.?题型一题型二题型三题型四求曲线的切线方程 (1)求在曲线C上横坐标为2的点处的切线方程.
(2)第(1)小题中的切线与曲线C是否还有其他的公共点?
分析解答第(1)小题,可先求出切点坐标及斜率,然后利用直线的点斜式方程求切线方程;解答第(2)小题,可把第(1)小题中求得的直线方程与已知的曲线方程组成方程组,求方程组的解.题型一题型二题型三题型四题型一题型二题型三题型四?反思1.解决这类题,先求出函数y=f(x)在已知点处的导数即曲线在该点处切线的斜率,再由直线的点斜式方程便可求出切线方程.
2.导数的几何意义中所说的点应在曲线上,否则函数在该点处的导数不是斜率.题型一题型二题型三题型四【变式训练1】 已知曲线C:f(x)=2x2+1,求过点P(0,0)且与曲线C相切的切线l的方程.?题型一题型二题型三题型四?题型一题型二题型三题型四求切点坐标
【例2】 已知抛物线y=f(x)=3x2+7,求:
(1)在抛物线上哪一点处的切线的倾斜角为45°?
(2)在抛物线上哪一点处的切线平行于直线6x-y-2=0?
(3)在抛物线上哪一点处的切线垂直于直线x+12y-3=0?
分析:设点的坐标→求出在该点处的导数→
利用条件建立方程→求出点的坐标题型一题型二题型三题型四?题型一题型二题型三题型四(2)因为切线平行于直线6x-y-2=0,
所以切线的斜率为6,即f'(x0)=6x0=6,得x0=1.
所以该点的坐标为(1,10).
(3)因为切线与直线x+12y-3=0垂直,
所以切线的斜率为12,即f'(x0)=6x0=12,得x0=2.
所以该点的坐标为(2,19).题型一题型二题型三题型四反思解答此类题目,所给的直线的倾斜角或斜率是解题的关键,由这些信息可知函数在所求点处的导数,进而可求得此点的横坐标.
具体的解题步骤为:
(1)先设切点坐标为(x0,y0);
(2)求导函数f'(x);
(3)求切线的斜率;
(4)由斜率与导数间的关系列出关于x0的方程,解方程求x0;
(5)切点(x0,y0)在曲线f(x)上,将(x0,y0)代入曲线方程求得切点坐标.题型一题型二题型三题型四【变式训练2】 求曲线y=f(x)=x3在哪一点处的切线,
(1)平行于直线y=3x-5?
(2)垂直于直线x+6y+5=0?
(3)倾斜角为45°?
分析:本题主要考查导数的几何意义和两条直线平行、垂直的条件.解题的关键是设出切点的坐标,求出切线的斜率.题型一题型二题型三题型四?题型一题型二题型三题型四导数几何意义的综合应用
【例3】 设曲线f(x)=x2+1和g(x)=x3+x在其交点处的两条切线的夹角为θ,求cos θ.
分析:本题考查了导数几何意义的综合应用,解决本题的关键是求出两条切线的方向向量,要求cos θ的值,必须先求出两条曲线的交点,再利用导数分别求出在交点处的切线的斜率,通过向量的数量积可求得cos θ.题型一题型二题型三题型四?题型一题型二题型三题型四?反思导数几何意义的综合应用,主要是根据函数y=f(x)在x=x0处的导数即曲线f(x)在x=x0处的切线的斜率去求切点坐标及切线方程,再利用题中所提供的诸如斜率的线性关系、斜率的最值、斜率的范围、直线的方向向量等关系求解相关问题.题型一题型二题型三题型四?题型一题型二题型三题型四题型一题型二题型三题型四?题型一题型二题型三题型四错因分析:在求切线方程时,一定要注意是求过某一点的切线方程还是求在某点处的切线方程.前者可能会有多个结果,而后者通常只有一个结果.题型一题型二题型三题型四反思1.求在某点处的切线,该点就是切点,因此可直接求出切线斜率(该点处导数的值),写出切线方程.
2.求过某点的切线,要注意该点不一定是切点.
因此,在解题时先设出切点,再求出切线斜率(该点处导数的值),根据切点与斜率写出切线方程,最后再将该点坐标代入.在解题过程中不必考虑该点是否为切点.
2.会求导函数.
3.根据导数的几何意义,会求曲线上某点处的切线方程.??名师点拨如图,函数f(x)在区间[x0,x0+Δx]上的平均变化率的几何意义是割线PQ的斜率,当点Q沿曲线y=f(x)趋近于点P时(即Δx趋近于0),割线PQ绕点P转动,它的最终位置为曲线在点P处的切线位置——直线PT.?【做一做1-1】 若f'(x0)=0,则曲线y=f(x)在点(x0,f(x0))处的切线( )
A.不存在
B.与x轴平行或重合
C.与x轴垂直
D.与x轴斜交
解析:由导数的几何意义知,曲线y=f(x)在点(x0,f(x0))处的切线斜率为0,故选B.
答案:B??【做一做2-2】 若曲线f(x)的导函数为f'(x)=2x+3,则f'(3)等于( )
A.0 B.2 C.3 D.9
答案:D【做一做2-1】 函数在某一点处的导数是( )
A.在该点的函数值的改变量与自变量的改变量的比
B.一个函数
C.一个常数,不是变数
D.函数在这一点与它附近一点之间的平均变化率
解析:根据函数在一点处的导数的定义,可知选C.
答案:C?2.“用割线的极限位置来定义切线”和“与曲线只有一个公共点的直线是切线”的区别是什么?
剖析:在初中我们学习过圆的切线:当直线和圆有唯一公共点时,我们称直线和圆相切,这时直线叫做圆的切线,唯一的公共点叫做切点,圆是一种特殊的曲线.如果将圆的切线推广为一般曲线的切线:当直线和曲线有唯一公共点时,直线叫做曲线过该点的切线,这种推广是不妥当的.观察图中的曲线C,直线l1虽然与曲线C有唯一的公共点M,但我们不能说直线l1与曲线C相切;而直线l2尽管与曲线C有不止一个公共点,我们还是说直线l2是曲线C在点N处的切线.因此,对于一般的曲线,必须重新寻求曲线切线的定义.?题型一题型二题型三题型四求曲线的切线方程 (1)求在曲线C上横坐标为2的点处的切线方程.
(2)第(1)小题中的切线与曲线C是否还有其他的公共点?
分析解答第(1)小题,可先求出切点坐标及斜率,然后利用直线的点斜式方程求切线方程;解答第(2)小题,可把第(1)小题中求得的直线方程与已知的曲线方程组成方程组,求方程组的解.题型一题型二题型三题型四题型一题型二题型三题型四?反思1.解决这类题,先求出函数y=f(x)在已知点处的导数即曲线在该点处切线的斜率,再由直线的点斜式方程便可求出切线方程.
2.导数的几何意义中所说的点应在曲线上,否则函数在该点处的导数不是斜率.题型一题型二题型三题型四【变式训练1】 已知曲线C:f(x)=2x2+1,求过点P(0,0)且与曲线C相切的切线l的方程.?题型一题型二题型三题型四?题型一题型二题型三题型四求切点坐标
【例2】 已知抛物线y=f(x)=3x2+7,求:
(1)在抛物线上哪一点处的切线的倾斜角为45°?
(2)在抛物线上哪一点处的切线平行于直线6x-y-2=0?
(3)在抛物线上哪一点处的切线垂直于直线x+12y-3=0?
分析:设点的坐标→求出在该点处的导数→
利用条件建立方程→求出点的坐标题型一题型二题型三题型四?题型一题型二题型三题型四(2)因为切线平行于直线6x-y-2=0,
所以切线的斜率为6,即f'(x0)=6x0=6,得x0=1.
所以该点的坐标为(1,10).
(3)因为切线与直线x+12y-3=0垂直,
所以切线的斜率为12,即f'(x0)=6x0=12,得x0=2.
所以该点的坐标为(2,19).题型一题型二题型三题型四反思解答此类题目,所给的直线的倾斜角或斜率是解题的关键,由这些信息可知函数在所求点处的导数,进而可求得此点的横坐标.
具体的解题步骤为:
(1)先设切点坐标为(x0,y0);
(2)求导函数f'(x);
(3)求切线的斜率;
(4)由斜率与导数间的关系列出关于x0的方程,解方程求x0;
(5)切点(x0,y0)在曲线f(x)上,将(x0,y0)代入曲线方程求得切点坐标.题型一题型二题型三题型四【变式训练2】 求曲线y=f(x)=x3在哪一点处的切线,
(1)平行于直线y=3x-5?
(2)垂直于直线x+6y+5=0?
(3)倾斜角为45°?
分析:本题主要考查导数的几何意义和两条直线平行、垂直的条件.解题的关键是设出切点的坐标,求出切线的斜率.题型一题型二题型三题型四?题型一题型二题型三题型四导数几何意义的综合应用
【例3】 设曲线f(x)=x2+1和g(x)=x3+x在其交点处的两条切线的夹角为θ,求cos θ.
分析:本题考查了导数几何意义的综合应用,解决本题的关键是求出两条切线的方向向量,要求cos θ的值,必须先求出两条曲线的交点,再利用导数分别求出在交点处的切线的斜率,通过向量的数量积可求得cos θ.题型一题型二题型三题型四?题型一题型二题型三题型四?反思导数几何意义的综合应用,主要是根据函数y=f(x)在x=x0处的导数即曲线f(x)在x=x0处的切线的斜率去求切点坐标及切线方程,再利用题中所提供的诸如斜率的线性关系、斜率的最值、斜率的范围、直线的方向向量等关系求解相关问题.题型一题型二题型三题型四?题型一题型二题型三题型四题型一题型二题型三题型四?题型一题型二题型三题型四错因分析:在求切线方程时,一定要注意是求过某一点的切线方程还是求在某点处的切线方程.前者可能会有多个结果,而后者通常只有一个结果.题型一题型二题型三题型四反思1.求在某点处的切线,该点就是切点,因此可直接求出切线斜率(该点处导数的值),写出切线方程.
2.求过某点的切线,要注意该点不一定是切点.
因此,在解题时先设出切点,再求出切线斜率(该点处导数的值),根据切点与斜率写出切线方程,最后再将该点坐标代入.在解题过程中不必考虑该点是否为切点.
