1.3.1 函数的单调性与导数 课件(25张PPT)
文档属性
| 名称 | 1.3.1 函数的单调性与导数 课件(25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 957.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-10 09:37:33 | ||
图片预览








文档简介
课件25张PPT。1.3.1 函数的单调性与导数
1.结合实例,直观探索并掌握函数的单调性与导数的关系.
2.能利用导数研究函数的单调性.
3.会求函数的单调区间(其中多项式函数一般不超过三次).1.一般地,函数的单调性与其导函数的正负有如下关系:在某个区间(a,b)内,如果f'(x)>0,那么函数y=f(x)在这个区间内单调递增;如果f'(x)<0,那么函数y=f(x)在这个区间内单调递减.名师点拨用曲线的切线的斜率来理解单调性与导函数的关系:当切线斜率为正时,切线的倾斜角小于90°,函数曲线呈向上增加状态;当切线斜率为负时,切线的倾斜角大于90°且小于180°,函数曲线呈向下减少状态.【做一做1】 函数f(x)=5x3-15x的单调递增区间是( )
A.(-∞,-1),(1,+∞) B.(-∞,-1)
C.(1,+∞) D.(-1,1)
答案:A2.一般地,如果一个函数在某一范围内导数的绝对值较大,那么函数在这个范围内变化得快,这时,函数的图象就比较“陡峭”(向上或向下);反之,函数的图象就“平缓”一些.名师点拨通过函数图象,不仅可以看出函数的单调性,还可以看出函数变化的快慢.
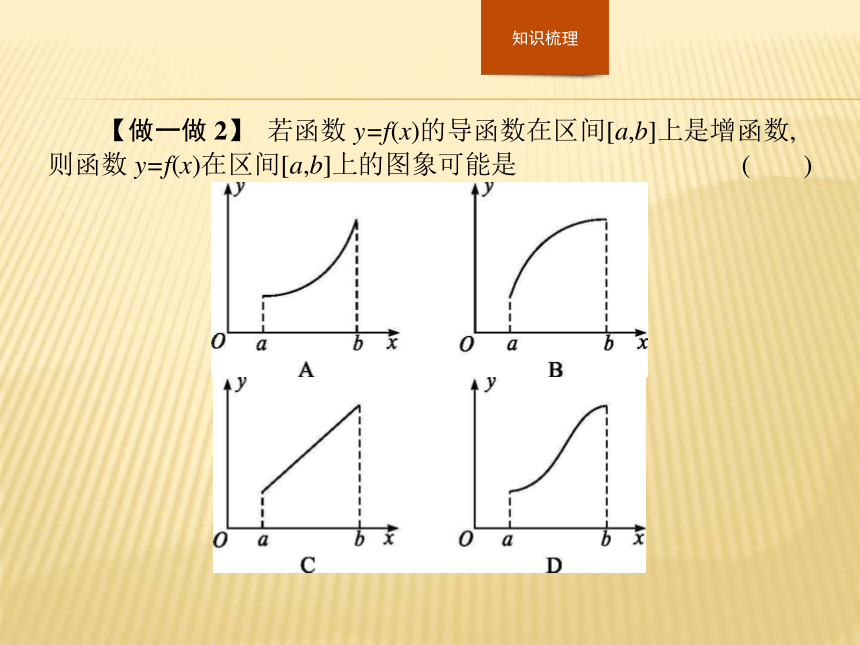
“函数变化快慢与其导数的关系”如下:解析:因为y=f(x)的导函数在区间[a,b]内是增函数,所以从左到右函数f(x)图象上的点处的切线斜率是递增的.
答案:A1.如何理解函数的单调性与导数的关系?
剖析:(1)在利用导数来讨论函数的单调区间时,先要确定函数的定义域,再在定义域内通过讨论导数的符号来判断函数的单调区间.
(2)一般利用使导数等于零的点来划分函数的单调区间.
(3)若函数在某个区间内恒有f'(x)=0,则f(x)在此区间内为常数函数.如f(x)=3,则f'(x)=3'=0.
(4)利用导数的符号判断函数的增减性,这是导数在研究曲线变化规律中的一个应用,它充分体现了数形结合思想.名师点拨对于可导函数f(x)来说,“f'(x)>0”是“f(x)在(a,b)内单调递增”的充分不必要条件,“f'(x)<0”是“f(x)在(a,b)内单调递减”的充分不必要条件.例如f(x)=x3在R上为增函数,但f'(0)=0,所以在x=0处不满足f'(x)>0.2.求可导函数单调区间的一般步骤是什么?
剖析:第一步,确定函数f(x)的定义域.
第二步,求f'(x),令f'(x)=0,解此方程,求出它在定义域内的一切实根.
第三步,把函数f(x)在间断点(即f(x)的无定义点)的横坐标和上面的各实根按从小到大的顺序排列起来,然后用这些点把函数f(x)的定义域分成若干个小区间.
第四步,确定f'(x)在各个小区间内的符号,根据f'(x)的符号判定函数f(x)在每个相应小区间内的增减性.3.已知函数的单调性,如何求参数的取值范围?
剖析“f'(x)>0(或f'(x)<0)”是“函数单调递增(或单调递减)”的充分条件,但这个条件并不是必要的.在(a,b)内可导的函数f(x)在(a,b)内单调递增(或单调递减)的充要条件是f'(x)≥0(或f'(x)≤0)恒成立,且f'(x)在(a,b)的任意子区间内都不恒等于0.这就是说,函数f(x)在区间上的单调性并不排斥在区间内个别点处有f'(x0)=0,甚至可以在无穷多个点处f'(x0)=0,只是这样的点不能充满所给区间的任何一个子区间.因此,在已知函数f(x)单调递增(或单调递减)的条件下求参数的取值范围时,应令f'(x)≥0(或f'(x)≤0)恒成立,解出参数的取值范围(一般可用不等式恒成立来求解),然后检验参数的取值能否使f'(x)在所给区间的任何一个子区间内不恒为零,从而求得参数的取值范围.题型一题型二题型三题型四?题型一题型二题型三题型四由f(x)有唯一的一个负零点,可知f(x)=0有唯一的一个负实根.
综上可知,函数图象的大致形状如图所示.题型一题型二题型三题型四反思在研究一个函数的图象与其导函数的图象之间的关系时,要注意抓住各自的关键要素.对原函数,我们重点考察其图象在哪个区间内单调递增,在哪个区间内单调递减;而对于导函数,则应考察其函数值在哪个区间内大于零,在哪个区间内小于零,并考察这些区间与原函数的单调区间是否一致.题型一题型二题型三题型四解析:由f(x)的增减性与f'(x)的正负之间的关系进行判断,当x∈(2,4)时,f'(x)<0,故f(x)在(2,4)内单调递减,其他判断均错,故选C.
答案:C题型一题型二题型三题型四求函数的单调区间
【例2】 求下列函数的单调区间:
(1)f(x)=x3-x;
(2)f(x)=3x2-2ln x.
分析:解答本题需先确定函数的定义域,然后对函数求导,求解不等式f'(x)>0,f'(x)<0,并与定义域求交集得到相应的单调区间.题型一题型二题型三题型四题型一题型二题型三题型四反思1.当f(x)不含参数时,可通过解不等式f'(x)>0(或f'(x)<0)直接得到单调递增(或递减)区间.
2.当求得的单调区间不止一个时,单调区间之间要用“,”隔开,或用“和”相连.题型一题型二题型三题型四题型一题型二题型三题型四?题型一题型二题型三题型四?题型一题型二题型三题型四?题型一题型二题型三题型四题型一题型二题型三题型四反思先由函数f(x)在区间(a,b)内单调递增(递减)推出f'(x)≥0(f'(x)≤0)在区间(a,b)内恒成立,再利用分离参数或函数性质求解恒成立问题,对等号成立可单独验证说明.题型一题型二题型三题型四?题型一题型二题型三题型四?反思在解题中,常常会将必要条件作充分条件或将既不充分也不必要条件作充要条件等使用而导致错误,这需要在学习过程中注意思维的严密性.
2.能利用导数研究函数的单调性.
3.会求函数的单调区间(其中多项式函数一般不超过三次).1.一般地,函数的单调性与其导函数的正负有如下关系:在某个区间(a,b)内,如果f'(x)>0,那么函数y=f(x)在这个区间内单调递增;如果f'(x)<0,那么函数y=f(x)在这个区间内单调递减.名师点拨用曲线的切线的斜率来理解单调性与导函数的关系:当切线斜率为正时,切线的倾斜角小于90°,函数曲线呈向上增加状态;当切线斜率为负时,切线的倾斜角大于90°且小于180°,函数曲线呈向下减少状态.【做一做1】 函数f(x)=5x3-15x的单调递增区间是( )
A.(-∞,-1),(1,+∞) B.(-∞,-1)
C.(1,+∞) D.(-1,1)
答案:A2.一般地,如果一个函数在某一范围内导数的绝对值较大,那么函数在这个范围内变化得快,这时,函数的图象就比较“陡峭”(向上或向下);反之,函数的图象就“平缓”一些.名师点拨通过函数图象,不仅可以看出函数的单调性,还可以看出函数变化的快慢.
“函数变化快慢与其导数的关系”如下:解析:因为y=f(x)的导函数在区间[a,b]内是增函数,所以从左到右函数f(x)图象上的点处的切线斜率是递增的.
答案:A1.如何理解函数的单调性与导数的关系?
剖析:(1)在利用导数来讨论函数的单调区间时,先要确定函数的定义域,再在定义域内通过讨论导数的符号来判断函数的单调区间.
(2)一般利用使导数等于零的点来划分函数的单调区间.
(3)若函数在某个区间内恒有f'(x)=0,则f(x)在此区间内为常数函数.如f(x)=3,则f'(x)=3'=0.
(4)利用导数的符号判断函数的增减性,这是导数在研究曲线变化规律中的一个应用,它充分体现了数形结合思想.名师点拨对于可导函数f(x)来说,“f'(x)>0”是“f(x)在(a,b)内单调递增”的充分不必要条件,“f'(x)<0”是“f(x)在(a,b)内单调递减”的充分不必要条件.例如f(x)=x3在R上为增函数,但f'(0)=0,所以在x=0处不满足f'(x)>0.2.求可导函数单调区间的一般步骤是什么?
剖析:第一步,确定函数f(x)的定义域.
第二步,求f'(x),令f'(x)=0,解此方程,求出它在定义域内的一切实根.
第三步,把函数f(x)在间断点(即f(x)的无定义点)的横坐标和上面的各实根按从小到大的顺序排列起来,然后用这些点把函数f(x)的定义域分成若干个小区间.
第四步,确定f'(x)在各个小区间内的符号,根据f'(x)的符号判定函数f(x)在每个相应小区间内的增减性.3.已知函数的单调性,如何求参数的取值范围?
剖析“f'(x)>0(或f'(x)<0)”是“函数单调递增(或单调递减)”的充分条件,但这个条件并不是必要的.在(a,b)内可导的函数f(x)在(a,b)内单调递增(或单调递减)的充要条件是f'(x)≥0(或f'(x)≤0)恒成立,且f'(x)在(a,b)的任意子区间内都不恒等于0.这就是说,函数f(x)在区间上的单调性并不排斥在区间内个别点处有f'(x0)=0,甚至可以在无穷多个点处f'(x0)=0,只是这样的点不能充满所给区间的任何一个子区间.因此,在已知函数f(x)单调递增(或单调递减)的条件下求参数的取值范围时,应令f'(x)≥0(或f'(x)≤0)恒成立,解出参数的取值范围(一般可用不等式恒成立来求解),然后检验参数的取值能否使f'(x)在所给区间的任何一个子区间内不恒为零,从而求得参数的取值范围.题型一题型二题型三题型四?题型一题型二题型三题型四由f(x)有唯一的一个负零点,可知f(x)=0有唯一的一个负实根.
综上可知,函数图象的大致形状如图所示.题型一题型二题型三题型四反思在研究一个函数的图象与其导函数的图象之间的关系时,要注意抓住各自的关键要素.对原函数,我们重点考察其图象在哪个区间内单调递增,在哪个区间内单调递减;而对于导函数,则应考察其函数值在哪个区间内大于零,在哪个区间内小于零,并考察这些区间与原函数的单调区间是否一致.题型一题型二题型三题型四解析:由f(x)的增减性与f'(x)的正负之间的关系进行判断,当x∈(2,4)时,f'(x)<0,故f(x)在(2,4)内单调递减,其他判断均错,故选C.
答案:C题型一题型二题型三题型四求函数的单调区间
【例2】 求下列函数的单调区间:
(1)f(x)=x3-x;
(2)f(x)=3x2-2ln x.
分析:解答本题需先确定函数的定义域,然后对函数求导,求解不等式f'(x)>0,f'(x)<0,并与定义域求交集得到相应的单调区间.题型一题型二题型三题型四题型一题型二题型三题型四反思1.当f(x)不含参数时,可通过解不等式f'(x)>0(或f'(x)<0)直接得到单调递增(或递减)区间.
2.当求得的单调区间不止一个时,单调区间之间要用“,”隔开,或用“和”相连.题型一题型二题型三题型四题型一题型二题型三题型四?题型一题型二题型三题型四?题型一题型二题型三题型四?题型一题型二题型三题型四题型一题型二题型三题型四反思先由函数f(x)在区间(a,b)内单调递增(递减)推出f'(x)≥0(f'(x)≤0)在区间(a,b)内恒成立,再利用分离参数或函数性质求解恒成立问题,对等号成立可单独验证说明.题型一题型二题型三题型四?题型一题型二题型三题型四?反思在解题中,常常会将必要条件作充分条件或将既不充分也不必要条件作充要条件等使用而导致错误,这需要在学习过程中注意思维的严密性.
