人教新课标A版选修2-2第三章 数系的扩充与复数的引入3.1.2 复数的几何意义(20张PPT)
文档属性
| 名称 | 人教新课标A版选修2-2第三章 数系的扩充与复数的引入3.1.2 复数的几何意义(20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 967.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-09 00:00:00 | ||
图片预览








文档简介
课件20张PPT。3.1.2 复数的几何意义
1.了解复数的几何意义.
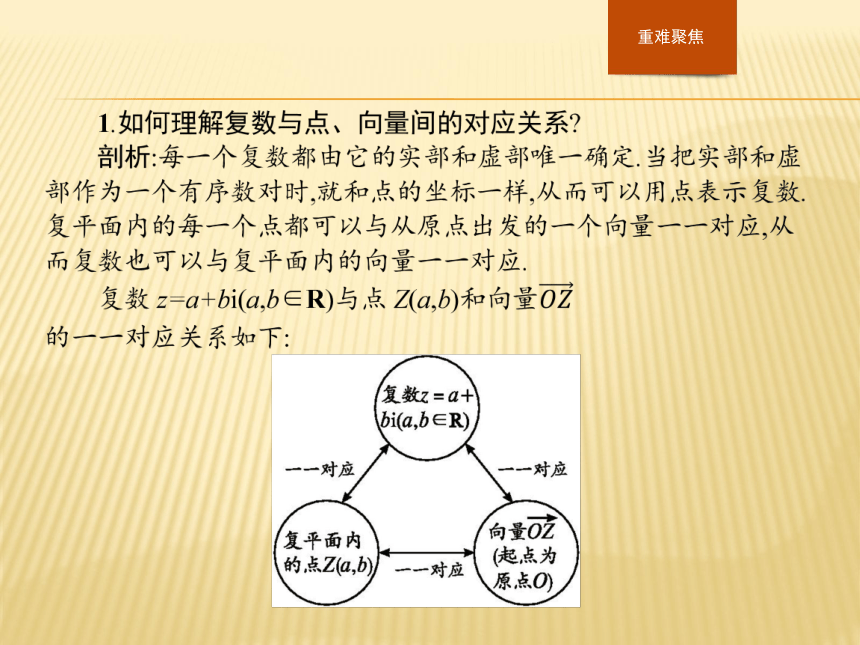
2.理解复数的模的概念,会求复数的模.?题型一题型二题型三题型一题型二题型三题型一题型二题型三反思复数的几何意义包含两种情况:
(1)复数与复平面内点的对应:复数的实部、虚部分别是该点的横坐标、纵坐标,利用这一点,可把复数问题转化为平面内点的坐标问题.
(2)复数与复平面内向量的对应:复数的实部、虚部是对应向量的坐标,利用这一点,可把复数问题转化为向量问题.题型一题型二题型三题型一题型二题型三?反思复数一般不能比较大小,但复数的模可以比较大小.题型一题型二题型三?题型一题型二题型三题型一题型二题型三?反思1.利用模的定义,得到关于a的不等式,与利用复数相等的充要条件一样,都贯彻了复数问题实数化的思想,这是本章的一种重要思想方法.
2.从几何意义上理解,复数的模表示复数对应的点到原点的距离,所以|z|=r表示以原点为圆心,r为半径的圆.题型一题型二题型三【变式训练3】 设z=a+bi(a,b∈R),求在复平面内满足下列条件的点所组成的图形.
(1)|a|<2,且|b|<2;
(2)|z|≤2,且|b|>1;
(3)|z|=2,且a>b;
(4)1≤|z|≤2.
解:(1)在复平面内,满足不等式|a|<2的点组成的图形是位于两条平行直线x=±2之间的长条带状(不包括两条平行直线).满足不等式|b|<2的点组成的图形是位于两条平行直线y=±2之间的长条带状(不包括两条平行直线),两者的公共部分即为所求.故满足条件的点所组成的图形是以原点为中心,边长等于4,各边分别平行于坐标轴的正方形内部的点,但不包括边界,如图①所示.题型一题型二题型三(2)不等式|z|≤2的解集对应的点是以原点为圆心,以2为半径的圆的内部及其边界上的点组成的图形.满足条件|b|>1的点是直线y=1以上及直线y=-1以下的点,两者的公共部分即为所求.故满足条件的点所组成的图形是以原点为圆心、以2为半径的圆被直线y=±1所截得的两个弓形,但不包括弦上的点,如图②所示.
(3)方程|z|=2对应点的集合是以原点为圆心,以2为半径的圆周.满足条件a>b的点组成的图形是位于直线y=x下方的半平面,其中不包括直线y=x上的点.两者的公共部分即为所求,如图③所示.题型一题型二题型三
2.理解复数的模的概念,会求复数的模.?题型一题型二题型三题型一题型二题型三题型一题型二题型三反思复数的几何意义包含两种情况:
(1)复数与复平面内点的对应:复数的实部、虚部分别是该点的横坐标、纵坐标,利用这一点,可把复数问题转化为平面内点的坐标问题.
(2)复数与复平面内向量的对应:复数的实部、虚部是对应向量的坐标,利用这一点,可把复数问题转化为向量问题.题型一题型二题型三题型一题型二题型三?反思复数一般不能比较大小,但复数的模可以比较大小.题型一题型二题型三?题型一题型二题型三题型一题型二题型三?反思1.利用模的定义,得到关于a的不等式,与利用复数相等的充要条件一样,都贯彻了复数问题实数化的思想,这是本章的一种重要思想方法.
2.从几何意义上理解,复数的模表示复数对应的点到原点的距离,所以|z|=r表示以原点为圆心,r为半径的圆.题型一题型二题型三【变式训练3】 设z=a+bi(a,b∈R),求在复平面内满足下列条件的点所组成的图形.
(1)|a|<2,且|b|<2;
(2)|z|≤2,且|b|>1;
(3)|z|=2,且a>b;
(4)1≤|z|≤2.
解:(1)在复平面内,满足不等式|a|<2的点组成的图形是位于两条平行直线x=±2之间的长条带状(不包括两条平行直线).满足不等式|b|<2的点组成的图形是位于两条平行直线y=±2之间的长条带状(不包括两条平行直线),两者的公共部分即为所求.故满足条件的点所组成的图形是以原点为中心,边长等于4,各边分别平行于坐标轴的正方形内部的点,但不包括边界,如图①所示.题型一题型二题型三(2)不等式|z|≤2的解集对应的点是以原点为圆心,以2为半径的圆的内部及其边界上的点组成的图形.满足条件|b|>1的点是直线y=1以上及直线y=-1以下的点,两者的公共部分即为所求.故满足条件的点所组成的图形是以原点为圆心、以2为半径的圆被直线y=±1所截得的两个弓形,但不包括弦上的点,如图②所示.
(3)方程|z|=2对应点的集合是以原点为圆心,以2为半径的圆周.满足条件a>b的点组成的图形是位于直线y=x下方的半平面,其中不包括直线y=x上的点.两者的公共部分即为所求,如图③所示.题型一题型二题型三
