人教新课标A版选修2-3第二章 随机变量及其分布2.4 正态分布(24张PPT)
文档属性
| 名称 | 人教新课标A版选修2-3第二章 随机变量及其分布2.4 正态分布(24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 556.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-09 10:52:06 | ||
图片预览








文档简介
课件24张PPT。2.4 正态分布1.了解正态分布的意义.
2.借助正态曲线理解正态分布的性质.
3.了解正态曲线的意义和性质.
4.会利用φ(x),F(x)的意义求正态总体小于X的概率.123412342.正态分布
一般地,如果对于任何实数a,b(a正态分布完全由参数μ和σ确定,因此正态分布常记作N(μ,σ2).
知识拓展1.参数μ是反映随机变量取值的平均水平的特征数,可以用样本均值去估计;σ是衡量随机变量总体波动大小的特征数,可以用样本标准差去估计.把μ=0,σ=1的正态分布叫做标准正态分布.
2.正态分布是自然界中最常见的一种分布,许多现象都近似地服从正态分布.如长度测量误差,正常生产条件下各种产品的质量指标等.1234答案:B 12343.正态曲线的特点
(1)曲线位于x轴上方,与x轴不相交.
(2)曲线是单峰的,它关于直线x=μ对称.
(4)曲线与x轴之间的面积为1.
(5)当σ一定时,曲线位置由μ确定,曲线随着μ的变化而沿x轴平移.
(6)当μ一定时,曲线的形状由σ确定,σ越小,曲线越“瘦高”,表示总体的分布越集中;σ越大,曲线越“矮胖”,表示总体的分布越分散.1234知识拓展 1234【做一做2】 设随机变量ξ~N(μ,σ2),且P(ξ≤C)=P(ξ>C),则C等于( )
A.0 B.σ
C.-μ D.μ
解析:正态分布在x=μ对称的区间上概率相等,则C=μ.
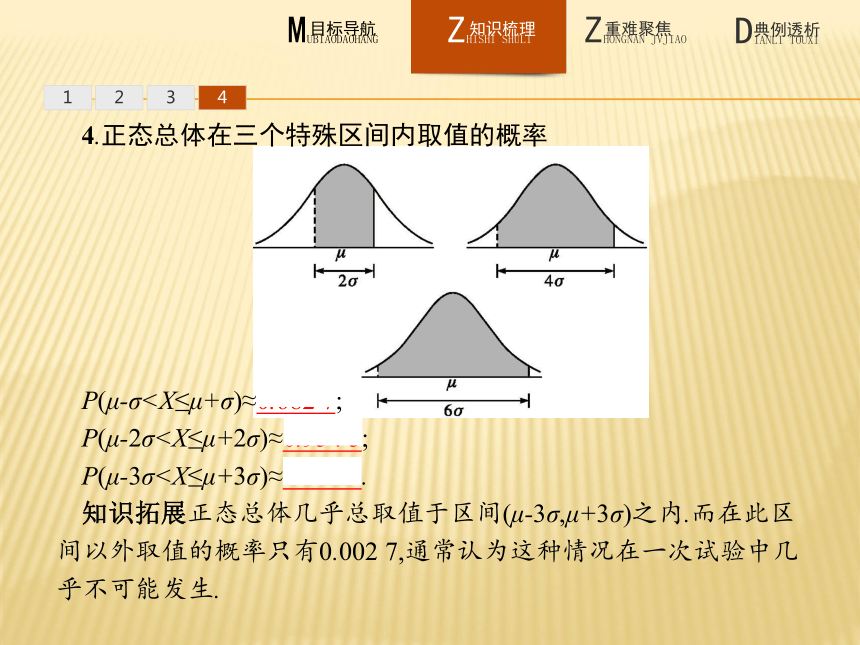
答案:D12344.正态总体在三个特殊区间内取值的概率
P(μ-σP(μ-2σP(μ-3σ知识拓展正态总体几乎总取值于区间(μ-3σ,μ+3σ)之内.而在此区间以外取值的概率只有0.002 7,通常认为这种情况在一次试验中几乎不可能发生.121.如何求服从正态分布的随机变量X在某区间内取值的概率
剖析首先找出随机变量X服从正态分布时μ,σ的值,再利用3σ原则求随机变量X在某一个区间上取值的概率,最后利用随机变量X在关于X=μ对称的区间上取值的概率相等求得结果.122.正态总体在某个区间内取值概率的求解策略
剖析(1)充分利用正态曲线的对称性和曲线与x轴之间面积为1.
(2)熟记P(μ-σ(3)注意概率值的求解转化:
①P(X②P(X<μ-a)=P(X≥μ+a);题型一题型二题型三题型四【例1】 如图是一条正态曲线,试根据图象写出该正态分布密度曲线的函数解析式,求出总体随机变量的均值和方差.
分析该曲线的对称轴和最高点从图中容易看出,从而求出总体随机变量的均值、标准差以及正态曲线的函数解析式.题型一题型二题型三题型四反思1.要特别注意方差是标准差的平方.
2.用待定系数法求正态分布密度曲线的函数表达式,关键是确定参数μ与σ的值.
3.当x=μ时,正态分布密度曲线的函数取得最大值,即
注意该式在解题中的运用.题型一题型二题型三题型四【变式训练1】 关于正态曲线特点的描述:
①曲线关于直线x=μ对称,这条曲线在x轴上方;
②曲线关于直线x=σ对称,这条曲线只有当x∈(-3σ,3σ)时才在x轴上方;
③曲线关于y轴对称,因为曲线对应的正态分布密度函数是一个偶函数;
④曲线在x=μ时处于最高点,由这一点向左右两边延伸时,曲线逐渐降低;
⑤曲线的对称轴由μ确定,曲线的形状由σ确定;
⑥σ越大,曲线越“矮胖”;σ越小,曲线越“高瘦”.
说法正确的是( )
A.①④⑤⑥ B.②④⑤ C.③④⑤⑥ D.①⑤⑥题型一题型二题型三题型四解析:参照正态曲线的性质,正态曲线位于x轴上方,且只有当μ=0时,正态曲线才关于y轴对称,因此知A选项正确.
答案:A题型一题型二题型三题型四【例2】 设ξ~N(1,4),试求:
(1)P(-1<ξ≤3);
(2)P(3<ξ≤5);
(3)P(ξ≥5).
分析首先确定μ,σ,然后根据正态曲线的对称性和P(μ-σ(1)求证:P(1(2)若P(X≤2)=a,求P(10(1)证明∵X~N(10,1),
∴正态曲线φμ,σ(x)关于直线x=10对称,
而区间(1,2)和(18,19)关于直线x=10对称,
即P(1∴P(X≤2)=P(X≥18)=a,P(2分析欲判定这批零件是否合格,关键是看随机抽查的一件产品的尺寸是在(μ-3σ,μ+3σ)内,还是在(μ-3σ,μ+3σ)之外.
解:由于圆柱形零件的外径X~N(4,0.25),由正态分布的特征可知,正态分布N(4,0.25)在区间(4-3×0.5,4+3×0.5)即(2.5,5.5)之外取值的概率只有0.002 7,而5.7?(2.5,5.5),这说明在一次试验中,出现了几乎不可能发生的小概率事件,故可以认为该厂生产的这批产品是不合格的.题型一题型二题型三题型四反思在试验应用中,通常认为服从正态分布N(μ,σ2)的随机变量X只取(μ-3σ,μ+3σ)之间的值,并简称为3σ原则.如果服从正态分布的随机变量的某些取值超出了这个范围,就说明出现了意外情况.题型一题型二题型三题型四【变式训练3】 一建筑工地所需要的钢筋的长度服从正态分布,其中μ=8,σ=2.质检员在检查一大批钢筋的质量时发现有的钢筋长度小于2 m.这时,他让钢筋工继续用钢筋切割机切割钢筋,还是让钢筋工停止生产,检修钢筋切割机?
解:设检验出钢筋长为x m,则x<2.
由题意X~N(μ,σ2),其中μ=8,σ=2,则μ-3σ=2,μ+3σ=14.因为x?(2,14),
所以这一钢筋的长度出现在区间(μ-3σ,μ+3σ)之外,所以检验员应马上让钢筋工停止生产,立即检修钢筋切割机.题型一题型二题型三题型四易错点:混淆密度函数中μ,σ意义而致错
【例4】 把一条正态曲线C1沿着横轴方向向右移动2个单位长度,得到一条新的曲线C2,下列说法不正确的是( )
A.曲线C2仍是正态曲线
B.曲线C1,C2的最高点的纵坐标相等
C.以曲线C2为正态曲线的总体的方差比以曲线C1为正态曲线的总体的方差大2
D.以曲线C2为正态曲线的总体的均值比以曲线C1为正态曲线的总体的均值大2
错解:D
错因分析把正态密度函数中μ,σ的意义混淆了.题型一题型二题型三题型四度后,曲线形状没变,仍为正态曲线,且最高点的纵坐标f(μ)没变,从而σ没变,所以方差没变,而平移前后对称轴变了,即μ变了,因为曲线向右平移2个单位长度,所以均值μ增大了2个单位长度.
答案:C
反思正态曲线的左右平移只改变其均值的大小,不改变方差的大小.也就是平移变换不改变随机变量的方差,只有沿y轴方向的伸缩变换才改变其方差.
2.借助正态曲线理解正态分布的性质.
3.了解正态曲线的意义和性质.
4.会利用φ(x),F(x)的意义求正态总体小于X的概率.123412342.正态分布
一般地,如果对于任何实数a,b(a
知识拓展1.参数μ是反映随机变量取值的平均水平的特征数,可以用样本均值去估计;σ是衡量随机变量总体波动大小的特征数,可以用样本标准差去估计.把μ=0,σ=1的正态分布叫做标准正态分布.
2.正态分布是自然界中最常见的一种分布,许多现象都近似地服从正态分布.如长度测量误差,正常生产条件下各种产品的质量指标等.1234答案:B 12343.正态曲线的特点
(1)曲线位于x轴上方,与x轴不相交.
(2)曲线是单峰的,它关于直线x=μ对称.
(4)曲线与x轴之间的面积为1.
(5)当σ一定时,曲线位置由μ确定,曲线随着μ的变化而沿x轴平移.
(6)当μ一定时,曲线的形状由σ确定,σ越小,曲线越“瘦高”,表示总体的分布越集中;σ越大,曲线越“矮胖”,表示总体的分布越分散.1234知识拓展 1234【做一做2】 设随机变量ξ~N(μ,σ2),且P(ξ≤C)=P(ξ>C),则C等于( )
A.0 B.σ
C.-μ D.μ
解析:正态分布在x=μ对称的区间上概率相等,则C=μ.
答案:D12344.正态总体在三个特殊区间内取值的概率
P(μ-σ
剖析首先找出随机变量X服从正态分布时μ,σ的值,再利用3σ原则求随机变量X在某一个区间上取值的概率,最后利用随机变量X在关于X=μ对称的区间上取值的概率相等求得结果.122.正态总体在某个区间内取值概率的求解策略
剖析(1)充分利用正态曲线的对称性和曲线与x轴之间面积为1.
(2)熟记P(μ-σ
①P(X
分析该曲线的对称轴和最高点从图中容易看出,从而求出总体随机变量的均值、标准差以及正态曲线的函数解析式.题型一题型二题型三题型四反思1.要特别注意方差是标准差的平方.
2.用待定系数法求正态分布密度曲线的函数表达式,关键是确定参数μ与σ的值.
3.当x=μ时,正态分布密度曲线的函数取得最大值,即
注意该式在解题中的运用.题型一题型二题型三题型四【变式训练1】 关于正态曲线特点的描述:
①曲线关于直线x=μ对称,这条曲线在x轴上方;
②曲线关于直线x=σ对称,这条曲线只有当x∈(-3σ,3σ)时才在x轴上方;
③曲线关于y轴对称,因为曲线对应的正态分布密度函数是一个偶函数;
④曲线在x=μ时处于最高点,由这一点向左右两边延伸时,曲线逐渐降低;
⑤曲线的对称轴由μ确定,曲线的形状由σ确定;
⑥σ越大,曲线越“矮胖”;σ越小,曲线越“高瘦”.
说法正确的是( )
A.①④⑤⑥ B.②④⑤ C.③④⑤⑥ D.①⑤⑥题型一题型二题型三题型四解析:参照正态曲线的性质,正态曲线位于x轴上方,且只有当μ=0时,正态曲线才关于y轴对称,因此知A选项正确.
答案:A题型一题型二题型三题型四【例2】 设ξ~N(1,4),试求:
(1)P(-1<ξ≤3);
(2)P(3<ξ≤5);
(3)P(ξ≥5).
分析首先确定μ,σ,然后根据正态曲线的对称性和P(μ-σ
∴正态曲线φμ,σ(x)关于直线x=10对称,
而区间(1,2)和(18,19)关于直线x=10对称,
即P(1
解:由于圆柱形零件的外径X~N(4,0.25),由正态分布的特征可知,正态分布N(4,0.25)在区间(4-3×0.5,4+3×0.5)即(2.5,5.5)之外取值的概率只有0.002 7,而5.7?(2.5,5.5),这说明在一次试验中,出现了几乎不可能发生的小概率事件,故可以认为该厂生产的这批产品是不合格的.题型一题型二题型三题型四反思在试验应用中,通常认为服从正态分布N(μ,σ2)的随机变量X只取(μ-3σ,μ+3σ)之间的值,并简称为3σ原则.如果服从正态分布的随机变量的某些取值超出了这个范围,就说明出现了意外情况.题型一题型二题型三题型四【变式训练3】 一建筑工地所需要的钢筋的长度服从正态分布,其中μ=8,σ=2.质检员在检查一大批钢筋的质量时发现有的钢筋长度小于2 m.这时,他让钢筋工继续用钢筋切割机切割钢筋,还是让钢筋工停止生产,检修钢筋切割机?
解:设检验出钢筋长为x m,则x<2.
由题意X~N(μ,σ2),其中μ=8,σ=2,则μ-3σ=2,μ+3σ=14.因为x?(2,14),
所以这一钢筋的长度出现在区间(μ-3σ,μ+3σ)之外,所以检验员应马上让钢筋工停止生产,立即检修钢筋切割机.题型一题型二题型三题型四易错点:混淆密度函数中μ,σ意义而致错
【例4】 把一条正态曲线C1沿着横轴方向向右移动2个单位长度,得到一条新的曲线C2,下列说法不正确的是( )
A.曲线C2仍是正态曲线
B.曲线C1,C2的最高点的纵坐标相等
C.以曲线C2为正态曲线的总体的方差比以曲线C1为正态曲线的总体的方差大2
D.以曲线C2为正态曲线的总体的均值比以曲线C1为正态曲线的总体的均值大2
错解:D
错因分析把正态密度函数中μ,σ的意义混淆了.题型一题型二题型三题型四度后,曲线形状没变,仍为正态曲线,且最高点的纵坐标f(μ)没变,从而σ没变,所以方差没变,而平移前后对称轴变了,即μ变了,因为曲线向右平移2个单位长度,所以均值μ增大了2个单位长度.
答案:C
反思正态曲线的左右平移只改变其均值的大小,不改变方差的大小.也就是平移变换不改变随机变量的方差,只有沿y轴方向的伸缩变换才改变其方差.
