三年级下册数学试题-第2单元 长方形和正方形的面积(含解析答案)西师大版
文档属性
| 名称 | 三年级下册数学试题-第2单元 长方形和正方形的面积(含解析答案)西师大版 |
|
|
| 格式 | zip | ||
| 文件大小 | 91.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-05 15:04:08 | ||
图片预览

文档简介
第2单元 长方形和正方形的面积
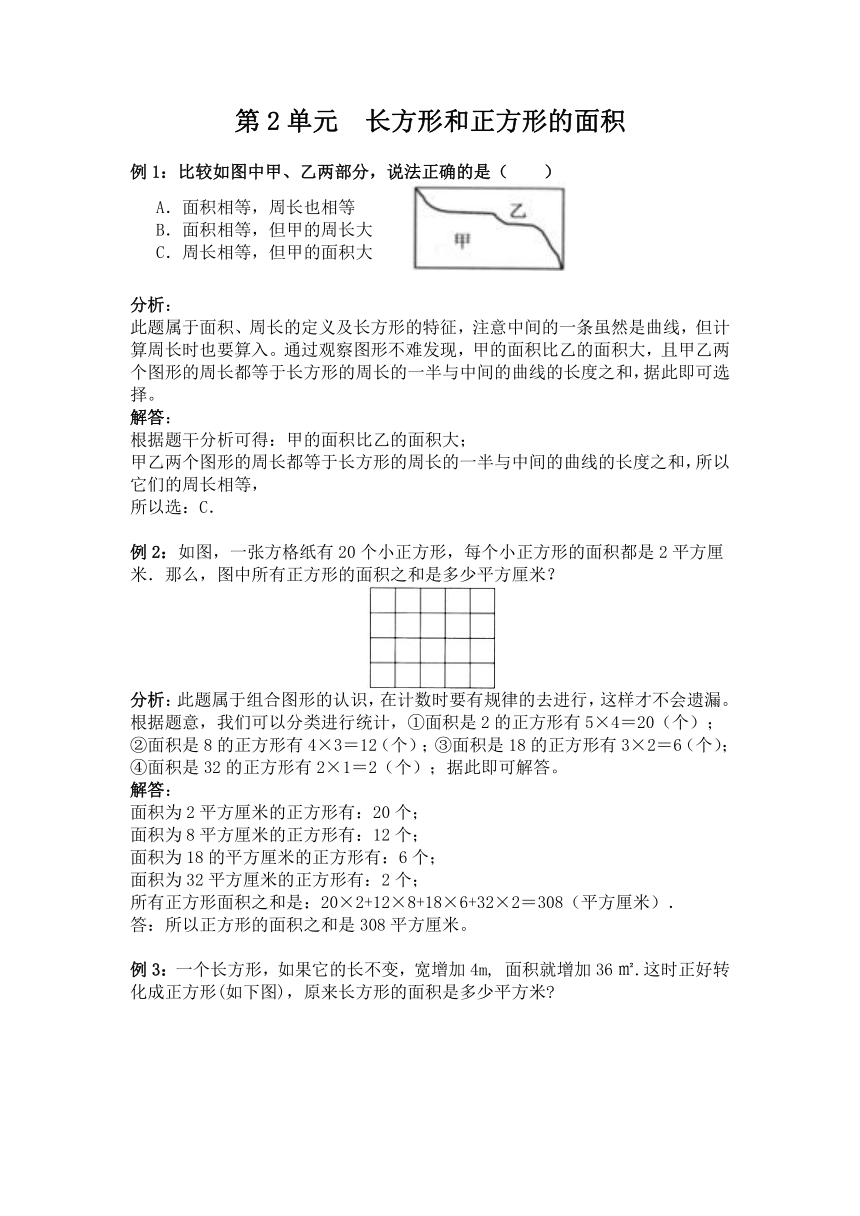
例1:比较如图中甲、乙两部分,说法正确的是( )
/
分析:
此题属于面积、周长的定义及长方形的特征,注意中间的一条虽然是曲线,但计算周长时也要算入。通过观察图形不难发现,甲的面积比乙的面积大,且甲乙两个图形的周长都等于长方形的周长的一半与中间的曲线的长度之和,据此即可选择。
解答:
根据题干分析可得:甲的面积比乙的面积大;
甲乙两个图形的周长都等于长方形的周长的一半与中间的曲线的长度之和,所以它们的周长相等,
所以选:C.
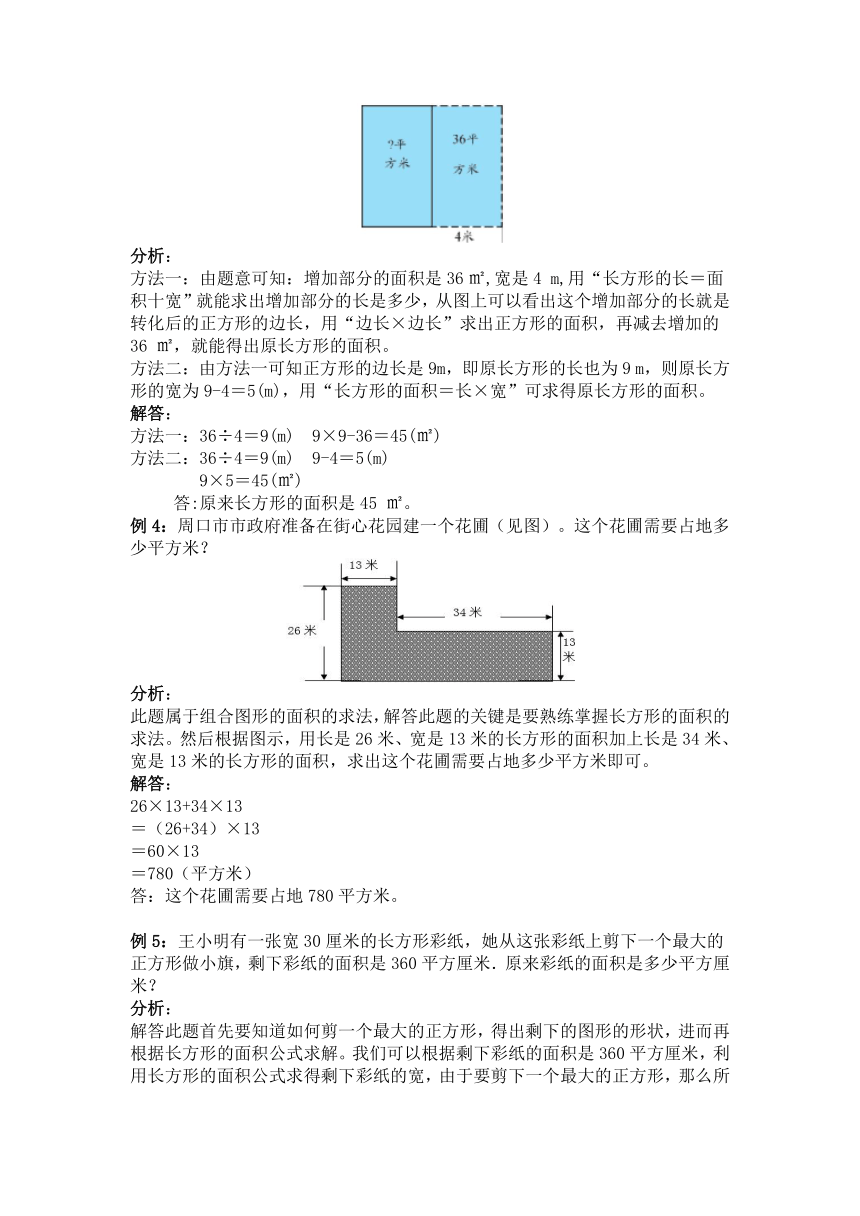
例2:如图,一张方格纸有20个小正方形,每个小正方形的面积都是2平方厘米.那么,图中所有正方形的面积之和是多少平方厘米?
/
分析:此题属于组合图形的认识,在计数时要有规律的去进行,这样才不会遗漏。
根据题意,我们可以分类进行统计,①面积是2的正方形有5×4=20(个);②面积是8的正方形有4×3=12(个);③面积是18的正方形有3×2=6(个);④面积是32的正方形有2×1=2(个);据此即可解答。
解答:
面积为2平方厘米的正方形有:20个;
面积为8平方厘米的正方形有:12个;
面积为18的平方厘米的正方形有:6个;
面积为32平方厘米的正方形有:2个;
所有正方形面积之和是:20×2+12×8+18×6+32×2=308(平方厘米).
答:所以正方形的面积之和是308平方厘米。
例3:一个长方形,如果它的长不变,宽增加4m, 面积就增加36㎡.这时正好转化成正方形(如下图),原来长方形的面积是多少平方米?
/
分析:
方法一:由题意可知:增加部分的面积是36㎡,宽是4 m,用“长方形的长=面积十宽”就能求出增加部分的长是多少,从图上可以看出这个增加部分的长就是转化后的正方形的边长,用“边长×边长”求出正方形的面积,再减去增加的36 ㎡,就能得出原长方形的面积。
方法二:由方法一可知正方形的边长是9m,即原长方形的长也为9 m,则原长方形的宽为9-4=5(m),用“长方形的面积=长×宽”可求得原长方形的面积。
解答:
方法一:36÷4=9(m) 9×9-36=45(㎡)
方法二:36÷4=9(m) 9-4=5(m)
9×5=45(㎡)
答:原来长方形的面积是45 ㎡。
例4:周口市市政府准备在街心花园建一个花圃(见图)。这个花圃需要占地多少平方米?
/
分析:
此题属于组合图形的面积的求法,解答此题的关键是要熟练掌握长方形的面积的求法。然后根据图示,用长是26米、宽是13米的长方形的面积加上长是34米、宽是13米的长方形的面积,求出这个花圃需要占地多少平方米即可。
解答:
26×13+34×13
=(26+34)×13
=60×13
=780(平方米)
答:这个花圃需要占地780平方米。
例5:王小明有一张宽30厘米的长方形彩纸,她从这张彩纸上剪下一个最大的正方形做小旗,剩下彩纸的面积是360平方厘米.原来彩纸的面积是多少平方厘米?
分析:
解答此题首先要知道如何剪一个最大的正方形,得出剩下的图形的形状,进而再根据长方形的面积公式求解。我们可以根据剩下彩纸的面积是360平方厘米,利用长方形的面积公式求得剩下彩纸的宽,由于要剪下一个最大的正方形,那么所剪的正方形的边长必须是长方形彩纸的宽30厘米,依此得到原来彩纸的长和宽,再根据长方形的面积公式解答。
解答:
360÷30=12(厘米)
30+12=42(厘米)
42×30=1260(平方厘米)
答:原来彩纸的面积是1260平方厘米。
例6:学校原有一块边长15米的正方形草坪,重新规划时,一条边增加3米,另一条边增加了5米,这样就变成了一个长方形,这个长方形草坪和原来相比,面积增加了多少平方米?(画图解答)
分析:
可以根据长方形和正方形的面积公式,用扩建后的长方形的面积减去原来正方形的面积即可。
解答:
如下图:
/
(15+5)×(15+3)-15×15
=20×18-225
=360-225
=135(平方米)
答:面积增加了135平方米。
例7:有一块小麦实验田,长为10米,宽50分米,这块实验田的面积是多少平方米?如果每平方米收小麦12千克,这块小麦实验田一共收小麦多少千克?
分析:
我们可以先依据长方形的面积公式:S=ab,求出实验田的面积,再乘12,即可得解.
解答:
50分米=5米
10×5=50(平方米)
50×12=600(千克).
答:这块实验田的面积是50平方米,这块小麦实验田一共收小麦600千克。
例8:图中的每个数字分别表示所对应的线段的长度(单位:米)。这个图形
的面积等于多少平方米?
/
分析:
我们可以将图形分割成若干个长方形,然后求出图形的面积,
(1)图形的面积等于下图中三个长方形的面积之和,三个长方形的长和宽从上到下分别是,长5米,宽2米;长(5+3)米,宽3米;长(5+3+4)米,宽2米,据此利用长方形的面积公式即可解决。
/
(2)图形的面积等于下图中三个长方形的面积之和,三个长方形的长和宽从左到右分别是,长(2+3+2)米,宽5米;长(2+3)米,宽3米;长4米,宽2米,据此利用长方形的面积公式即可解决。
/
我们也可以将图形添补成一个大长方形,然后利用大长方形与两个小长方形的
面积之差求出图形的面积。
(3)图形的面积等于下图中大个长方形减去两个小长方形的面积,三个长方形的长和宽从左到右分别是,长(5+3+4)米,宽(2+3+2)米;长2米,宽3米;长(2+3)米,宽4米,据此利用长方形的面积公式即可解决。
/
(4)图形的面积等于下图中大个长方形减去两个小长方形的面积,三个长方形的长和宽从左到右分别是,长(5+3+4)米,宽(2+3+2)米;长(3+4)米,宽2米;长4米,宽3米,据此利用长方形的面积公式即可解决。
/
解答:
(1)5×2+(5+3)×3+(5+3+4)×2=58(平方米)
(2)5×(2+3+2)+3×(2+3)+4×2=58(平方米)
(3)(5+3+4) × (2+3+2)-2×3-(2+3)×4=58(平方米)
(4)(5+3+4) ×(2+3+2)-2×(3+4)-3×4=58(平方米)
例9:在一个长50米,宽20米的长方形游泳池四周,铺上宽2米的防滑垫(如图),游泳池的面积是多少平方米??防滑垫的面积是多少平方米?
/
分析:
此题属于长方形的面积公式S=ab的实际应用;解题时要注意铺2米宽的防滑垫后长方形的长和宽都增加了4米。
(1)根据长方形的面积公式:S=ab,代入数据,列式解决问题;
(2)求出长是50+2+2米,宽是20+2+2米的长方形的面积,再减去游泳池的面积就是防滑垫的面积。
解答:
(1)50×20=1000(平方米)
(2)(50+2+2)×(20+2+2)-1000
=54×24-1000
=1296-1000
=296(平方米)
答:游泳池的面积是1000平方米,防滑垫的面积是296平方米.
例10:一张长方形纸,长90cm,宽60cm,把它分成边长是3dm的正方形,可分成多少个正方形?
分析:
本题的单位不统一,我们可以先统一单位,然后求出长方形纸的面积,再求出小正方形的面积,最后用长方形的面积除以小正方形的面积。
解答:
90cm=9dm 60cm=6dm
9×6=54(dm2)3×3=9(dm2)
54÷=6(个)
答:可以分成6个边长为3dm的正方形。
例1:比较如图中甲、乙两部分,说法正确的是( )
/
分析:
此题属于面积、周长的定义及长方形的特征,注意中间的一条虽然是曲线,但计算周长时也要算入。通过观察图形不难发现,甲的面积比乙的面积大,且甲乙两个图形的周长都等于长方形的周长的一半与中间的曲线的长度之和,据此即可选择。
解答:
根据题干分析可得:甲的面积比乙的面积大;
甲乙两个图形的周长都等于长方形的周长的一半与中间的曲线的长度之和,所以它们的周长相等,
所以选:C.
例2:如图,一张方格纸有20个小正方形,每个小正方形的面积都是2平方厘米.那么,图中所有正方形的面积之和是多少平方厘米?
/
分析:此题属于组合图形的认识,在计数时要有规律的去进行,这样才不会遗漏。
根据题意,我们可以分类进行统计,①面积是2的正方形有5×4=20(个);②面积是8的正方形有4×3=12(个);③面积是18的正方形有3×2=6(个);④面积是32的正方形有2×1=2(个);据此即可解答。
解答:
面积为2平方厘米的正方形有:20个;
面积为8平方厘米的正方形有:12个;
面积为18的平方厘米的正方形有:6个;
面积为32平方厘米的正方形有:2个;
所有正方形面积之和是:20×2+12×8+18×6+32×2=308(平方厘米).
答:所以正方形的面积之和是308平方厘米。
例3:一个长方形,如果它的长不变,宽增加4m, 面积就增加36㎡.这时正好转化成正方形(如下图),原来长方形的面积是多少平方米?
/
分析:
方法一:由题意可知:增加部分的面积是36㎡,宽是4 m,用“长方形的长=面积十宽”就能求出增加部分的长是多少,从图上可以看出这个增加部分的长就是转化后的正方形的边长,用“边长×边长”求出正方形的面积,再减去增加的36 ㎡,就能得出原长方形的面积。
方法二:由方法一可知正方形的边长是9m,即原长方形的长也为9 m,则原长方形的宽为9-4=5(m),用“长方形的面积=长×宽”可求得原长方形的面积。
解答:
方法一:36÷4=9(m) 9×9-36=45(㎡)
方法二:36÷4=9(m) 9-4=5(m)
9×5=45(㎡)
答:原来长方形的面积是45 ㎡。
例4:周口市市政府准备在街心花园建一个花圃(见图)。这个花圃需要占地多少平方米?
/
分析:
此题属于组合图形的面积的求法,解答此题的关键是要熟练掌握长方形的面积的求法。然后根据图示,用长是26米、宽是13米的长方形的面积加上长是34米、宽是13米的长方形的面积,求出这个花圃需要占地多少平方米即可。
解答:
26×13+34×13
=(26+34)×13
=60×13
=780(平方米)
答:这个花圃需要占地780平方米。
例5:王小明有一张宽30厘米的长方形彩纸,她从这张彩纸上剪下一个最大的正方形做小旗,剩下彩纸的面积是360平方厘米.原来彩纸的面积是多少平方厘米?
分析:
解答此题首先要知道如何剪一个最大的正方形,得出剩下的图形的形状,进而再根据长方形的面积公式求解。我们可以根据剩下彩纸的面积是360平方厘米,利用长方形的面积公式求得剩下彩纸的宽,由于要剪下一个最大的正方形,那么所剪的正方形的边长必须是长方形彩纸的宽30厘米,依此得到原来彩纸的长和宽,再根据长方形的面积公式解答。
解答:
360÷30=12(厘米)
30+12=42(厘米)
42×30=1260(平方厘米)
答:原来彩纸的面积是1260平方厘米。
例6:学校原有一块边长15米的正方形草坪,重新规划时,一条边增加3米,另一条边增加了5米,这样就变成了一个长方形,这个长方形草坪和原来相比,面积增加了多少平方米?(画图解答)
分析:
可以根据长方形和正方形的面积公式,用扩建后的长方形的面积减去原来正方形的面积即可。
解答:
如下图:
/
(15+5)×(15+3)-15×15
=20×18-225
=360-225
=135(平方米)
答:面积增加了135平方米。
例7:有一块小麦实验田,长为10米,宽50分米,这块实验田的面积是多少平方米?如果每平方米收小麦12千克,这块小麦实验田一共收小麦多少千克?
分析:
我们可以先依据长方形的面积公式:S=ab,求出实验田的面积,再乘12,即可得解.
解答:
50分米=5米
10×5=50(平方米)
50×12=600(千克).
答:这块实验田的面积是50平方米,这块小麦实验田一共收小麦600千克。
例8:图中的每个数字分别表示所对应的线段的长度(单位:米)。这个图形
的面积等于多少平方米?
/
分析:
我们可以将图形分割成若干个长方形,然后求出图形的面积,
(1)图形的面积等于下图中三个长方形的面积之和,三个长方形的长和宽从上到下分别是,长5米,宽2米;长(5+3)米,宽3米;长(5+3+4)米,宽2米,据此利用长方形的面积公式即可解决。
/
(2)图形的面积等于下图中三个长方形的面积之和,三个长方形的长和宽从左到右分别是,长(2+3+2)米,宽5米;长(2+3)米,宽3米;长4米,宽2米,据此利用长方形的面积公式即可解决。
/
我们也可以将图形添补成一个大长方形,然后利用大长方形与两个小长方形的
面积之差求出图形的面积。
(3)图形的面积等于下图中大个长方形减去两个小长方形的面积,三个长方形的长和宽从左到右分别是,长(5+3+4)米,宽(2+3+2)米;长2米,宽3米;长(2+3)米,宽4米,据此利用长方形的面积公式即可解决。
/
(4)图形的面积等于下图中大个长方形减去两个小长方形的面积,三个长方形的长和宽从左到右分别是,长(5+3+4)米,宽(2+3+2)米;长(3+4)米,宽2米;长4米,宽3米,据此利用长方形的面积公式即可解决。
/
解答:
(1)5×2+(5+3)×3+(5+3+4)×2=58(平方米)
(2)5×(2+3+2)+3×(2+3)+4×2=58(平方米)
(3)(5+3+4) × (2+3+2)-2×3-(2+3)×4=58(平方米)
(4)(5+3+4) ×(2+3+2)-2×(3+4)-3×4=58(平方米)
例9:在一个长50米,宽20米的长方形游泳池四周,铺上宽2米的防滑垫(如图),游泳池的面积是多少平方米??防滑垫的面积是多少平方米?
/
分析:
此题属于长方形的面积公式S=ab的实际应用;解题时要注意铺2米宽的防滑垫后长方形的长和宽都增加了4米。
(1)根据长方形的面积公式:S=ab,代入数据,列式解决问题;
(2)求出长是50+2+2米,宽是20+2+2米的长方形的面积,再减去游泳池的面积就是防滑垫的面积。
解答:
(1)50×20=1000(平方米)
(2)(50+2+2)×(20+2+2)-1000
=54×24-1000
=1296-1000
=296(平方米)
答:游泳池的面积是1000平方米,防滑垫的面积是296平方米.
例10:一张长方形纸,长90cm,宽60cm,把它分成边长是3dm的正方形,可分成多少个正方形?
分析:
本题的单位不统一,我们可以先统一单位,然后求出长方形纸的面积,再求出小正方形的面积,最后用长方形的面积除以小正方形的面积。
解答:
90cm=9dm 60cm=6dm
9×6=54(dm2)3×3=9(dm2)
54÷=6(个)
答:可以分成6个边长为3dm的正方形。
