人教版九年级物理 17.4欧姆定律在串、并联电路中的应用 教案
文档属性
| 名称 | 人教版九年级物理 17.4欧姆定律在串、并联电路中的应用 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 41.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2019-12-07 07:30:59 | ||
图片预览

文档简介
第四节 欧姆定律在串并联电路中的应用
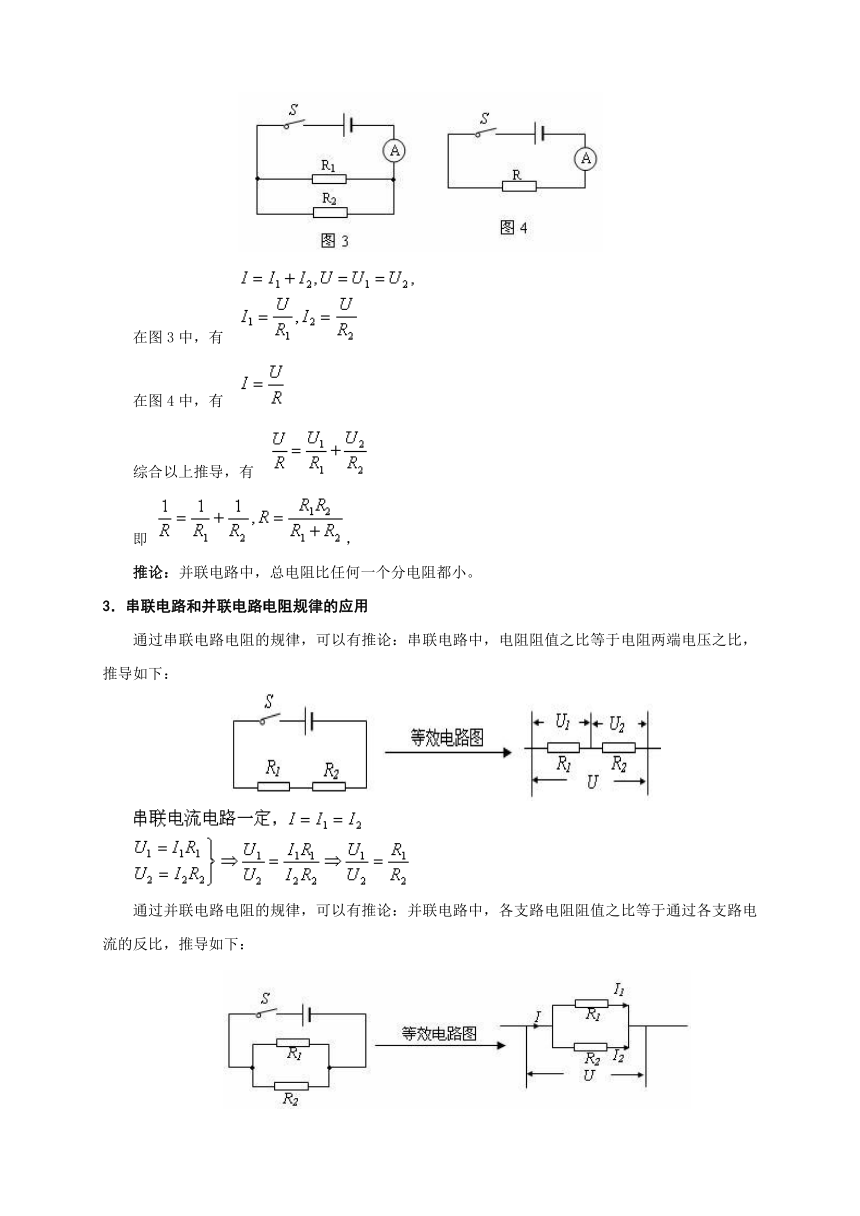
一、知识和技能要求 1. 理解欧姆定律,能运用欧姆定律进行简单的计算; 2. 能根据欧姆定律以及电路的特点,得出串、并联电路中电阻的关系。 二、重点难点精析 1. 等效电阻 在电路中,如果一个电阻的效果和几个电阻在同一电路中的效果相同,可以认为这个电阻是几个电阻的等效电阻。这个概念可以结合“合力与分力的关系”对照理解。 电阻在电路中的作用即对电流的阻碍作用。这里的“等效”可以理解为在同一个电路中,即电源电压相同,电阻对电流的阻碍作用相同,电路中的电流大小相同。 如果电源电压相同,在图1和图2中电流表示数相同,可以认为R为R1和R2串联后的等效电阻,也称总电阻。 2. 串联、并联电路中等效电阻与各分电阻的关系 (1)串联电路 在图1中,因为R1和R2串联,因此通过它们的电流相同,设R1两端电压为U1,R2两端电压为U2,则有 , 图2中有:, 综合以上推导,有:, 因此可以得到有串联电路总电阻和分电阻的关系: , 推论:串联电路的总电阻比任何一个分电阻都大。 (2) 并联电路 等效电阻电路如图3、图4所示。两个图中电流表示数相同,说明R和R1、R2并联的效果相同,可以认为R是其等效电阻。 在图3中,有 在图4中,有 综合以上推导,有 即 , 推论:并联电路中,总电阻比任何一个分电阻都小。 3.串联电路和并联电路电阻规律的应用 通过串联电路电阻的规律,可以有推论:串联电路中,电阻阻值之比等于电阻两端电压之比,推导如下: 通过并联电路电阻的规律,可以有推论:并联电路中,各支路电阻阻值之比等于通过各支路电流的反比,推导如下: 三、典型例题 1:一只灯泡两端的电压是3V,能正常发光,此时的电阻是6Ω。如果把这只灯泡接到电压为9V的电源上,电路中应串联一个多大的电阻,灯泡才能正常发光? 分析与解: 解电路题时,需要先把题中描述的等效电路图画好。通过题中叙述可知,电源电压高于灯泡正常发光所需要的电压,因此需要串联一个电阻分担电源电压。此电路是一个串联电路。在等效电路中标出必要字母和数据。 电路问题中,关键是解决各电阻的阻值问题。解答串联电路电阻问题时一般有三种解法。 解法一:常规解法。 即根据公式,分别找到电阻两端的电压和通过电阻的电流,再算出电阻的大小,解法如下。 解法二: 通过串联电路的电阻规律:,计算出串联电路总电阻和其中一个电阻,再算出另一个电阻,具体解法如下。 解法三: 利用串联电路中电阻和电压成正比,,只需要分别找出两个电阻两端电压的比值,即可直接算出待求电阻的大小。 电学中由于公式之间的互通性,因此一题多解常常出现,需要多加练习。一般来说,在题目中最方便快捷的方法就是比例法。 2:如图所示电源电压9伏,电阻R1=6欧,通过R1的电流是0.5安,干路中的电流是2安,求电阻R2的阻值,和R1、R2的等效电阻? 分析与解: 初看此题,可以发现实质上这是一个混联电路,超过初中电学的要求。但是仔细审题可以发现其实需要解决的问题都在并联部分,和混联无关,因此这道题可以看成一道并联的题。由于滑动变阻器阻值不为0,因此电源电压和并联部分的电压一定不同,题中告诉电源电压值对解中道题没有帮助,是一个迷惑条件。 此题也至少可以用两种方法求解。 解法一:常规解法,即算出电阻两端电压和电流再算出电阻,具体解法如下。 解法二: 利用并联电路中,通过各支路的电流之比和各支路电阻的比值成反比,具体解法如下。
一、知识和技能要求 1. 理解欧姆定律,能运用欧姆定律进行简单的计算; 2. 能根据欧姆定律以及电路的特点,得出串、并联电路中电阻的关系。 二、重点难点精析 1. 等效电阻 在电路中,如果一个电阻的效果和几个电阻在同一电路中的效果相同,可以认为这个电阻是几个电阻的等效电阻。这个概念可以结合“合力与分力的关系”对照理解。 电阻在电路中的作用即对电流的阻碍作用。这里的“等效”可以理解为在同一个电路中,即电源电压相同,电阻对电流的阻碍作用相同,电路中的电流大小相同。 如果电源电压相同,在图1和图2中电流表示数相同,可以认为R为R1和R2串联后的等效电阻,也称总电阻。 2. 串联、并联电路中等效电阻与各分电阻的关系 (1)串联电路 在图1中,因为R1和R2串联,因此通过它们的电流相同,设R1两端电压为U1,R2两端电压为U2,则有 , 图2中有:, 综合以上推导,有:, 因此可以得到有串联电路总电阻和分电阻的关系: , 推论:串联电路的总电阻比任何一个分电阻都大。 (2) 并联电路 等效电阻电路如图3、图4所示。两个图中电流表示数相同,说明R和R1、R2并联的效果相同,可以认为R是其等效电阻。 在图3中,有 在图4中,有 综合以上推导,有 即 , 推论:并联电路中,总电阻比任何一个分电阻都小。 3.串联电路和并联电路电阻规律的应用 通过串联电路电阻的规律,可以有推论:串联电路中,电阻阻值之比等于电阻两端电压之比,推导如下: 通过并联电路电阻的规律,可以有推论:并联电路中,各支路电阻阻值之比等于通过各支路电流的反比,推导如下: 三、典型例题 1:一只灯泡两端的电压是3V,能正常发光,此时的电阻是6Ω。如果把这只灯泡接到电压为9V的电源上,电路中应串联一个多大的电阻,灯泡才能正常发光? 分析与解: 解电路题时,需要先把题中描述的等效电路图画好。通过题中叙述可知,电源电压高于灯泡正常发光所需要的电压,因此需要串联一个电阻分担电源电压。此电路是一个串联电路。在等效电路中标出必要字母和数据。 电路问题中,关键是解决各电阻的阻值问题。解答串联电路电阻问题时一般有三种解法。 解法一:常规解法。 即根据公式,分别找到电阻两端的电压和通过电阻的电流,再算出电阻的大小,解法如下。 解法二: 通过串联电路的电阻规律:,计算出串联电路总电阻和其中一个电阻,再算出另一个电阻,具体解法如下。 解法三: 利用串联电路中电阻和电压成正比,,只需要分别找出两个电阻两端电压的比值,即可直接算出待求电阻的大小。 电学中由于公式之间的互通性,因此一题多解常常出现,需要多加练习。一般来说,在题目中最方便快捷的方法就是比例法。 2:如图所示电源电压9伏,电阻R1=6欧,通过R1的电流是0.5安,干路中的电流是2安,求电阻R2的阻值,和R1、R2的等效电阻? 分析与解: 初看此题,可以发现实质上这是一个混联电路,超过初中电学的要求。但是仔细审题可以发现其实需要解决的问题都在并联部分,和混联无关,因此这道题可以看成一道并联的题。由于滑动变阻器阻值不为0,因此电源电压和并联部分的电压一定不同,题中告诉电源电压值对解中道题没有帮助,是一个迷惑条件。 此题也至少可以用两种方法求解。 解法一:常规解法,即算出电阻两端电压和电流再算出电阻,具体解法如下。 解法二: 利用并联电路中,通过各支路的电流之比和各支路电阻的比值成反比,具体解法如下。
同课章节目录
- 第十三章 内能
- 第1节 分子热运动
- 第2节 内能
- 第3节 比热容
- 第十四章 内能的利用
- 第1节 热机
- 第2节 热机的效率
- 第3节 能量的转化和守恒
- 第十五章 电流和电路
- 第1节 两种电荷
- 第2节 电流和电路
- 第3节 串联和并联
- 第4节 电流的测量
- 第5节 串、并联电路中电流的规律
- 第十六章 电压 电阻
- 第1节 电压
- 第2节 串、并联电路电压的规律
- 第3节 电阻
- 第4节 变阻器
- 第十七章 欧姆定律
- 第1节 电流与电压和电阻的关系
- 第2节 欧姆定律
- 第3节 电阻的测量
- 第4节 欧姆定律在串、并联电路中的应用
- 第十八章 电功率
- 第1节 电能 电功
- 第2节 电功率
- 第3节 测量小灯泡的电功率
- 第4节 焦耳定律
- 第十九章 生活用电
- 第1节 家庭电路
- 第2节 家庭电路电流过大的原因
- 第3节 安全用电
- 第二十章 电与磁
- 第1节 磁现象 磁场
- 第2节 电生磁
- 第3节 电磁铁 电磁继电器
- 第4节 电动机
- 第5节 磁生电
- 第二十一章 信息的传递
- 第1节 现代顺风耳──电话
- 第2节 电磁波的海洋
- 第3节 广播、电视和移动通信
- 第4节 越来越宽的信息之路
- 第二十二章 能源与可持续发展
- 第1节 能源
- 第2节 核能
- 第3节 太阳能
- 第4节 能源与可持续发展
