四年级上册数学单元测试-8.不确定现象 西师大版(含答案)
文档属性
| 名称 | 四年级上册数学单元测试-8.不确定现象 西师大版(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 64.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-05 13:16:40 | ||
图片预览


文档简介
四年级上册数学单元测试-8.不确定现象
一、单选题
1.掷硬币的结果是(??? )
A.?正面朝上???????????????????????????????????B.?背面朝上???????????????????????????????????C.?不确定
2.哈尔滨的冬天(??? )会下雪
A.?一定????????????????????????????????????????B.?可能????????????????????????????????????????C.?不可能
3.盒子里有2个红球和5个黄球(球的大小、质地相同),任意摸出一个球,摸出红球的可能性是(? )
A.???????????????????????????????????????????B.???????????????????????????????????????????C.?
4.下列现象不可能发生的是(??????? )。
A.?太阳总是从东方升起???????????????B.?三天后下雨???????????????C.?在装满白色球的盒子里摸出红球
二、判断题
5.判断对错。 二十几加上二十几一定等于四十几。
6.判断 盒子里有9个红色棋子,2个黄色棋子,任意摸出一个,摸到的肯定是红色棋子.
7.张明抛6次硬币,3次正面向上,2次反面向上,他第6次抛硬币时正面向上的可能性是 .(判断对错)
8.箱子里放有4个红球和6个白球,若一次摸一个球,每次摸到红球的可能性是五分之二.(判断对错)
三、填空题
9.把一些白色围棋子放在书包里,从中任意摸出一个,________是白棋子。(填“可能”/“不可能”/“一定”)
10.如图,小明正在玩飞镖游戏,如果小明将飞镖随意投中如图所示的正方体木框中,那么投中阴影部分的可能性是________.
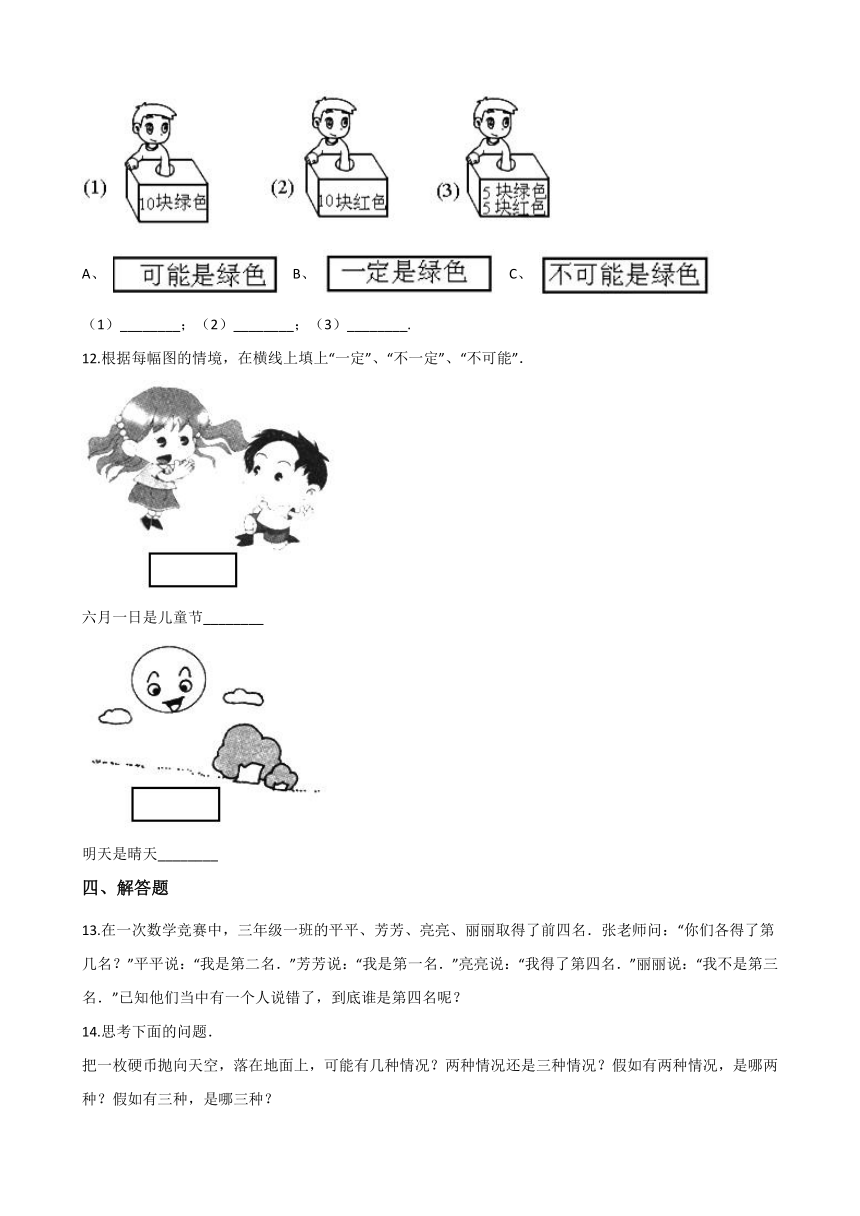
11.下面3个盒子里,每盒都放着10块水果糖,分别任意摸出1块,一定是绿色的吗?
A、 ?? B、 ?? C、 (1)________;(2)________;(3)________.
12.根据每幅图的情境,在横线上填上“一定”、“不一定”、“不可能”. 六月一日是儿童节________ 明天是晴天________
四、解答题
13.在一次数学竞赛中,三年级一班的平平、芳芳、亮亮、丽丽取得了前四名.张老师问:“你们各得了第几名?”平平说:“我是第二名.”芳芳说:“我是第一名.”亮亮说:“我得了第四名.”丽丽说:“我不是第三名.”已知他们当中有一个人说错了,到底谁是第四名呢?
14.思考下面的问题.
把一枚硬币抛向天空,落在地面上,可能有几种情况?两种情况还是三种情况?假如有两种情况,是哪两种?假如有三种,是哪三种?
五、综合题
15.下列哪些事件是确定的?哪些是不确定的?
(1)车辆随机经过一个路口,遇到红灯。
(2)三角形中有三条线段。
(3)400人中有两人的生日在同一天。
六、应用题
16.袋中有红球和白球各两个,任摸一次,小宁想摸到红球就一定能摸到吗?
参考答案
一、单选题
1.【答案】C
【解析】【解答】抛硬币的结果是不确定的 【分析】考查了判断事情的确定性和不确定性的能力
2.【答案】 A
【解析】【解答】哈尔滨的冬天一定会下雪,这是确定的事件 【分析】考查了判断事情的确定性和不确定性的能力
3.【答案】C
【解析】【解答】解:2+5=7(个),红球有2个,
所以摸出红球的可能性为:2÷7= .
故选:C.
【分析】求摸到红球的可能性,根据求可能性的方法:求一个数是另一个数的几分之几,用除法解答即可.解决此类问题的关键是分两种情况:(1)需要计算可能性的大小的准确值时,根据求可能性的方法:求一个数是另一个数的几分之几,用除法列式解答即可;(2)不需要计算可能性的大小的准确值时,可以根据各种球数量的多少,直接判断可能性的大小.
4.【答案】C
【解析】【解答】A.太阳总是从东方升起,是自然规律,属于确定事件中的一定事件;
B.三天后下雨,属于可能性中的不确定事件,在一定条件下可能发生,也可能不发生的事件;
C.在装满白色球的盒子里摸出红球,属于确定事件中的不可能事件,在装满白色球的盒子里不可能摸出红球,
故选:C.
【分析】“一定”表示确定事件,“可能”表示不确定事件,“不可能”属千确定事件中的必然事件,结合实际生活,按要求写出即可。
二、判断题
5.【答案】错误
【解析】【解答】解:因为二十几加上二十几可能等于四十几,可能等于五十几,如:23+25=48,28+26=54;所以二十几加上二十几一定等于四十几说法错误, 故答案为:错误。 【分析】根据事件的确定性与不确定性,确定性是一定发生的或不可能发生,不确定是可能发生的事,因为因为二十几加上二十几可能等于四十几,可能等于五十几;据此即可解答此题。
6.【答案】错误
【解析】【分析】摸到的可能是红色棋子,也可能是黄色棋子,不能说肯定是红色棋子。 【分析】盒子里每一个棋子被摸到的可能性是相等的,所以摸到的棋子可能是红色的,也可能是黄色的,只不过是红色棋子的数量较多,摸出的可能性较大。
7.【答案】 错误
【解析】【解答】解:1÷2=
答:第6次抛硬币时正面向上的可能性是 .
故答案为:错误.
【分析】首先根据随机事件发生的独立性,可得投掷第6次正面朝上的可能性与前5次结果无关;然后根据求可能性的方法:求一个数是另一个数的几分之几,用除法列式解答即可.此题主要考查了随机事件发生的独立性,根据求可能性的方法:求一个数是另一个数的几分之几,用除法列式解答即可.
8.【答案】 正确
【解析】【解答】解:4÷(4+6)=4÷10=
所以每次摸到红球的可能性是五分之二,题中说法正确.
故答案为:正确.
【分析】首先根据箱子里放有4个红球和6个白球,求出箱子中球的总量;然后根据求可能性的方法:求一个数是另一个数的几分之几,用除法列式解答,用红球的数量除以球的总量,求出每次摸到红球的可能性是多少即可.解决此类问题的关键是分两种情况:(1)需要计算可能性的大小的准确值时,根据求可能性的方法:求一个数是另一个数的几分之几,用除法列式解答即可;(2)不需要计算可能性的大小的准确值时,可以根据各种球数量的多少,直接判断可能性的大小.
三、填空题
9.【答案】一定
【解析】【解答】把一些白色围棋子放在书包里,从中任意摸出一个,一定是白棋子。 【分析】根据事件的确定性与不确定性,即得把一些白色围棋子放在书包里,从中任意摸出一个,一定是白棋子。
10.【答案】
【解析】【解答】解:设每个小正方形的面积是1,则每个大正方形的面积是36, 阴影部分的面积是: 2+2+3+3=10, 所以投中阴影部分的可能性是: 10÷36= . 答:投中阴影部分的可能性是 . 故答案为: . 【分析】首先设每个小正方形的面积是1,分别求出大正方形、阴影部分的面积是多少;然后根据求可能性的方法:求一个数是另一个数的几分之几,用除法列式解答,用阴影部分的面积除以大正方形的面积,求出投中阴影部分的可能性是多少即可.解答此类问题的关键是分两种情况:(1)需要计算可能性的大小的准确值时,根据求可能性的方法:求一个数是另一个数的几分之几,用除法列式解答即可;(2)不需要计算可能性的大小的准确值时,可以根据每种图形面积的大小,直接判断可能性的大小.
11.【答案】 B ;C ;A
【解析】【解答】解:(1)这个盒子里,放着的10块水果糖全是绿色的,摸出1块,一定是绿色的,不会是其它颜色;所以选B; (2)这个盒子里,放着的10块水果糖全是红色的,摸出1块,一定是红色的,不可能是绿色的;所以选C; (3)这个盒子里,放着的10块水果糖,5块是红色的,5块是绿色的,摸出1块,可能是红色的,也可能是绿色的;所以选A。 故答案为:(1)B;(2)C;(3)A。
【分析】根据事件的确定性与不确定性,确定性是一定发生的或不可能发生,不确定是可能发生的事,因为(1)盒子里放着的10块水果糖全是绿色的,摸出1块,一定是绿色的,不会是其它颜色;(2)盒子里放着的10块水果糖全是红色的,摸出1块,一定是红色的,不可能是绿色的;(3)盒子里放着的10块水果糖红色的和绿色的可能性;据此即可解答此题。
12.【答案】一定;不一定
【解析】【解答】
四、解答题
13.【答案】亮亮或丽丽是第四名
【解析】【解答】:解:假设平平、芳芳、亮亮说对了,丽丽说错了,第四名是亮亮;假设平平、芳芳、丽丽说对了,亮亮说错了,丽丽是第四名。 假设丽丽、芳芳、亮亮说对了,平平说错了,第四名是亮亮;假设平平、亮亮、丽丽说对了,芳芳说错了,第四名是亮亮。 故答案为:亮亮或丽丽是第四名。 【分析】本题关键是通过分析”亮亮说:“我得了第四名,对和错两种情况两种情况,说对时,亮亮是第四名,说错时丽丽是第四名。
14.【答案】 解:两种情况,正面和反面。
【解析】【分析】硬币只有两个面:正面和反面,把一枚硬币抛向天空,落在地面上,所能出现的情况只有正面朝上或者反面朝上两种情况。
五、综合题
15.【答案】(1)是不确定的 (2)是确定的 (3)是确定的
【解析】【分析】(1)路口的信号灯有3种状态:红灯、黄灯、绿灯,所以车辆随机经过一个路口,可能会遇到任何一种信号灯,遇到红灯是不确定的; (2)根据三角形的定义:由3条线段首尾相连围成的封闭图形叫三角形,可以得到任何一个三角形都有三条线段,这是确定的; (3)400÷365=1……35,至少有两人在同一天过生日,这是确定的.
六、应用题
16.【答案】解:根据分析可知,盒子中两种颜色的球数量相等,摸到的可能性相等,但是任意摸一次,不一定就能摸到自己想要的颜色,这是不确定的事件,所以任摸一次,小宁想摸到红球是不一定能摸到的. 答:任摸一次,小宁想摸到红球是不一定的.
【解析】【分析】可能性的大小与物体数量的多少有关,数量越多,摸到的可能性越大,数量越少,摸到的可能性越小,袋子中的两种球的数量相等,摸到的可能性相等,但是任意摸一次,不一定就能摸到自己想要的颜色,这是不确定的事件,据此判断.
一、单选题
1.掷硬币的结果是(??? )
A.?正面朝上???????????????????????????????????B.?背面朝上???????????????????????????????????C.?不确定
2.哈尔滨的冬天(??? )会下雪
A.?一定????????????????????????????????????????B.?可能????????????????????????????????????????C.?不可能
3.盒子里有2个红球和5个黄球(球的大小、质地相同),任意摸出一个球,摸出红球的可能性是(? )
A.???????????????????????????????????????????B.???????????????????????????????????????????C.?
4.下列现象不可能发生的是(??????? )。
A.?太阳总是从东方升起???????????????B.?三天后下雨???????????????C.?在装满白色球的盒子里摸出红球
二、判断题
5.判断对错。 二十几加上二十几一定等于四十几。
6.判断 盒子里有9个红色棋子,2个黄色棋子,任意摸出一个,摸到的肯定是红色棋子.
7.张明抛6次硬币,3次正面向上,2次反面向上,他第6次抛硬币时正面向上的可能性是 .(判断对错)
8.箱子里放有4个红球和6个白球,若一次摸一个球,每次摸到红球的可能性是五分之二.(判断对错)
三、填空题
9.把一些白色围棋子放在书包里,从中任意摸出一个,________是白棋子。(填“可能”/“不可能”/“一定”)
10.如图,小明正在玩飞镖游戏,如果小明将飞镖随意投中如图所示的正方体木框中,那么投中阴影部分的可能性是________.
11.下面3个盒子里,每盒都放着10块水果糖,分别任意摸出1块,一定是绿色的吗?
A、 ?? B、 ?? C、 (1)________;(2)________;(3)________.
12.根据每幅图的情境,在横线上填上“一定”、“不一定”、“不可能”. 六月一日是儿童节________ 明天是晴天________
四、解答题
13.在一次数学竞赛中,三年级一班的平平、芳芳、亮亮、丽丽取得了前四名.张老师问:“你们各得了第几名?”平平说:“我是第二名.”芳芳说:“我是第一名.”亮亮说:“我得了第四名.”丽丽说:“我不是第三名.”已知他们当中有一个人说错了,到底谁是第四名呢?
14.思考下面的问题.
把一枚硬币抛向天空,落在地面上,可能有几种情况?两种情况还是三种情况?假如有两种情况,是哪两种?假如有三种,是哪三种?
五、综合题
15.下列哪些事件是确定的?哪些是不确定的?
(1)车辆随机经过一个路口,遇到红灯。
(2)三角形中有三条线段。
(3)400人中有两人的生日在同一天。
六、应用题
16.袋中有红球和白球各两个,任摸一次,小宁想摸到红球就一定能摸到吗?
参考答案
一、单选题
1.【答案】C
【解析】【解答】抛硬币的结果是不确定的 【分析】考查了判断事情的确定性和不确定性的能力
2.【答案】 A
【解析】【解答】哈尔滨的冬天一定会下雪,这是确定的事件 【分析】考查了判断事情的确定性和不确定性的能力
3.【答案】C
【解析】【解答】解:2+5=7(个),红球有2个,
所以摸出红球的可能性为:2÷7= .
故选:C.
【分析】求摸到红球的可能性,根据求可能性的方法:求一个数是另一个数的几分之几,用除法解答即可.解决此类问题的关键是分两种情况:(1)需要计算可能性的大小的准确值时,根据求可能性的方法:求一个数是另一个数的几分之几,用除法列式解答即可;(2)不需要计算可能性的大小的准确值时,可以根据各种球数量的多少,直接判断可能性的大小.
4.【答案】C
【解析】【解答】A.太阳总是从东方升起,是自然规律,属于确定事件中的一定事件;
B.三天后下雨,属于可能性中的不确定事件,在一定条件下可能发生,也可能不发生的事件;
C.在装满白色球的盒子里摸出红球,属于确定事件中的不可能事件,在装满白色球的盒子里不可能摸出红球,
故选:C.
【分析】“一定”表示确定事件,“可能”表示不确定事件,“不可能”属千确定事件中的必然事件,结合实际生活,按要求写出即可。
二、判断题
5.【答案】错误
【解析】【解答】解:因为二十几加上二十几可能等于四十几,可能等于五十几,如:23+25=48,28+26=54;所以二十几加上二十几一定等于四十几说法错误, 故答案为:错误。 【分析】根据事件的确定性与不确定性,确定性是一定发生的或不可能发生,不确定是可能发生的事,因为因为二十几加上二十几可能等于四十几,可能等于五十几;据此即可解答此题。
6.【答案】错误
【解析】【分析】摸到的可能是红色棋子,也可能是黄色棋子,不能说肯定是红色棋子。 【分析】盒子里每一个棋子被摸到的可能性是相等的,所以摸到的棋子可能是红色的,也可能是黄色的,只不过是红色棋子的数量较多,摸出的可能性较大。
7.【答案】 错误
【解析】【解答】解:1÷2=
答:第6次抛硬币时正面向上的可能性是 .
故答案为:错误.
【分析】首先根据随机事件发生的独立性,可得投掷第6次正面朝上的可能性与前5次结果无关;然后根据求可能性的方法:求一个数是另一个数的几分之几,用除法列式解答即可.此题主要考查了随机事件发生的独立性,根据求可能性的方法:求一个数是另一个数的几分之几,用除法列式解答即可.
8.【答案】 正确
【解析】【解答】解:4÷(4+6)=4÷10=
所以每次摸到红球的可能性是五分之二,题中说法正确.
故答案为:正确.
【分析】首先根据箱子里放有4个红球和6个白球,求出箱子中球的总量;然后根据求可能性的方法:求一个数是另一个数的几分之几,用除法列式解答,用红球的数量除以球的总量,求出每次摸到红球的可能性是多少即可.解决此类问题的关键是分两种情况:(1)需要计算可能性的大小的准确值时,根据求可能性的方法:求一个数是另一个数的几分之几,用除法列式解答即可;(2)不需要计算可能性的大小的准确值时,可以根据各种球数量的多少,直接判断可能性的大小.
三、填空题
9.【答案】一定
【解析】【解答】把一些白色围棋子放在书包里,从中任意摸出一个,一定是白棋子。 【分析】根据事件的确定性与不确定性,即得把一些白色围棋子放在书包里,从中任意摸出一个,一定是白棋子。
10.【答案】
【解析】【解答】解:设每个小正方形的面积是1,则每个大正方形的面积是36, 阴影部分的面积是: 2+2+3+3=10, 所以投中阴影部分的可能性是: 10÷36= . 答:投中阴影部分的可能性是 . 故答案为: . 【分析】首先设每个小正方形的面积是1,分别求出大正方形、阴影部分的面积是多少;然后根据求可能性的方法:求一个数是另一个数的几分之几,用除法列式解答,用阴影部分的面积除以大正方形的面积,求出投中阴影部分的可能性是多少即可.解答此类问题的关键是分两种情况:(1)需要计算可能性的大小的准确值时,根据求可能性的方法:求一个数是另一个数的几分之几,用除法列式解答即可;(2)不需要计算可能性的大小的准确值时,可以根据每种图形面积的大小,直接判断可能性的大小.
11.【答案】 B ;C ;A
【解析】【解答】解:(1)这个盒子里,放着的10块水果糖全是绿色的,摸出1块,一定是绿色的,不会是其它颜色;所以选B; (2)这个盒子里,放着的10块水果糖全是红色的,摸出1块,一定是红色的,不可能是绿色的;所以选C; (3)这个盒子里,放着的10块水果糖,5块是红色的,5块是绿色的,摸出1块,可能是红色的,也可能是绿色的;所以选A。 故答案为:(1)B;(2)C;(3)A。
【分析】根据事件的确定性与不确定性,确定性是一定发生的或不可能发生,不确定是可能发生的事,因为(1)盒子里放着的10块水果糖全是绿色的,摸出1块,一定是绿色的,不会是其它颜色;(2)盒子里放着的10块水果糖全是红色的,摸出1块,一定是红色的,不可能是绿色的;(3)盒子里放着的10块水果糖红色的和绿色的可能性;据此即可解答此题。
12.【答案】一定;不一定
【解析】【解答】
四、解答题
13.【答案】亮亮或丽丽是第四名
【解析】【解答】:解:假设平平、芳芳、亮亮说对了,丽丽说错了,第四名是亮亮;假设平平、芳芳、丽丽说对了,亮亮说错了,丽丽是第四名。 假设丽丽、芳芳、亮亮说对了,平平说错了,第四名是亮亮;假设平平、亮亮、丽丽说对了,芳芳说错了,第四名是亮亮。 故答案为:亮亮或丽丽是第四名。 【分析】本题关键是通过分析”亮亮说:“我得了第四名,对和错两种情况两种情况,说对时,亮亮是第四名,说错时丽丽是第四名。
14.【答案】 解:两种情况,正面和反面。
【解析】【分析】硬币只有两个面:正面和反面,把一枚硬币抛向天空,落在地面上,所能出现的情况只有正面朝上或者反面朝上两种情况。
五、综合题
15.【答案】(1)是不确定的 (2)是确定的 (3)是确定的
【解析】【分析】(1)路口的信号灯有3种状态:红灯、黄灯、绿灯,所以车辆随机经过一个路口,可能会遇到任何一种信号灯,遇到红灯是不确定的; (2)根据三角形的定义:由3条线段首尾相连围成的封闭图形叫三角形,可以得到任何一个三角形都有三条线段,这是确定的; (3)400÷365=1……35,至少有两人在同一天过生日,这是确定的.
六、应用题
16.【答案】解:根据分析可知,盒子中两种颜色的球数量相等,摸到的可能性相等,但是任意摸一次,不一定就能摸到自己想要的颜色,这是不确定的事件,所以任摸一次,小宁想摸到红球是不一定能摸到的. 答:任摸一次,小宁想摸到红球是不一定的.
【解析】【分析】可能性的大小与物体数量的多少有关,数量越多,摸到的可能性越大,数量越少,摸到的可能性越小,袋子中的两种球的数量相等,摸到的可能性相等,但是任意摸一次,不一定就能摸到自己想要的颜色,这是不确定的事件,据此判断.
