人教九下数学27.2.1相似三角形的判定-教案
文档属性
| 名称 | 人教九下数学27.2.1相似三角形的判定-教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 368.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-06 10:56:54 | ||
图片预览




文档简介
27.2.1 相似三角形的判定
学习目标、重点、难点
【学习目标】
1.掌握两个三角形相似的判定条件(三个角对应相等,三条边的比对应相等,则两个三角形相似)——相似三角形的定义,和三角形相似的预备定理(平行于三角形一边的直线和其它两边相交,所构成的三角形与原三角形相似).
2.掌握“两组对应边的比相等且它们的夹角相等的两个三角形相似”的判定方法;掌握“两角对应相等,两个三角形相似”的判定方法.
3.会运用“两个三角形相似的判定条件”和“三角形相似的预备定理”解决简单的问题.
【重点难点】
1.相似三角形的定义与三角形相似的预备定理.
2.运用三角形相似的条件解决简单的问题.
知识概览图
定义及表示方法
两个三角形的三组对应边的比相等
两个三角形的两组对应边的比相等,并且它们的夹角相等
两个三角形有两对对应角相等
相似三角形的性质:对应角相等,对应边的比相等
新课导引
【生活链接】 小明为了迎接世界中学生数学大会的召开,制作了一个如右图所示形状的花束,三边长分别是35 cm,40 cm,50 cm,小丽也想制作一个这样形状的花束,但她手中只有一根长100 cm的木条,她应该怎么制作呢?
【问题探究】 如果两个多边形满足对应角相等,对应边的比相等,那么这两个多边形相似,但是定义中条件较多,过于苛刻,你能减少定义中的条件来判断两个三角形相似吗?
教材精华
知识点1 相似三角形
相似三角形是形状相同的三角形,它们的对应角都相等,对应边的比都相等.如图27—10所示,△ABC与△DEF的形状相同,大小不同,这两个三角形相似,所以∠A=∠D,∠B=∠E,∠C=∠F,·
拓展 相似三角形的定义既是最基本的判定方法,也是最重要的性质.
知识点2 相似三角形的表示方法
△ABC与△DEF相似,可以写成△ABC∽△DEF,也可以写成△DEF∽△ABC,读作“△ABC相似于△DEF”或“△DEF相似于△ABC”.
拓展 用“∽”这个符号表示两个图形相似时,对应的顶点应该写在对应的位置上,如图27-10所示,表示△ABC与△DEF相似,∠A的对应角是∠D,∠B的对应角是∠E,∠C的对应角是∠F,即△ABC∽△DEF,而不要写成△ABC∽△EFD,如果把△ABC写成△BAC,那么就应该记作△BAC∽△EDF,这样做的目的是为了指明对应角、对应边.
知识点3 三角形的相似比
两个三角形相似,对应边的比叫做相似比.
例如:若△ABC∽△DEF,则.设比值为k,于是k,即△ABC与△DEF的相似比为k.
拓展 这时△DEF与△ABC的相似比为.若BC=6,EF=8,则△ABC与△DEF的相似比为,△DEF与△ABC的相似比为.
探究交流 如果两个三角形的相似比k=1,那么这两个三角形有怎样的关系?
点拨 当两个三角形相似,且相似比为1时,这两个三角形全等,也就是说,这两个三角形的对应角都相等,对应边都相等,这两个三角形能够重合.三角形全等是三角形相似的特例.
知识点4 平行线分线段成比例定理
三条平行线截两条直线,所得的对应线段的比相等.
把这个定理应用到三角形中,可以得到:
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段的比相等.
知识点5 相似三角形的判定定理
判定定理1:平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
如图27—11所示,在△ABC中,过AB上一点D作DE∥BC交AC于点E,求证△ADE∽△ABC.
证明:∵DE∥BC,∴∠ADE=∠ABC,∠AED=∠ACB.
连接DC,BE,∵S△EBC=S△DBC,∴S△ABE=S△ACD.
∵同高的两个三角形面积的比等于底边的比,
∴.
∵.
如图27-12所示,过点D作DF∥AC交BC于点F.
易证
又∵BD=AB-AD,BF=BC-FC=BC-DE,
∴,即.
∴.
又∵∠A=∠A,∠ADE=∠ABC,∠AED=∠ACB,
∴△ADE∽△ABC.
判定定理2:如果两个三角形的三组对应边的比相等,那么这两个三角形相似.
如图27-13所示,在△ABC和△A′B′C′中,,求证△ABC∽△A′B′C′.
证明:在线段A′B′(或它的延长线)上截取A′D=AB,
过点D作DE∥B′C′交A′C′于点E,
∴△A′DE∽△A′B′C′,
∴.
又∵,A′D=AB,
∴.∴A′E=AC,同理DE=BC,
∴△A′DE≌△ABC(SSS),∴△ABC∽△A′B′C′.
例如:在△ABC与△A′B′C′中,AB=4 cm,BC=6 cm,AC=8 cm,A′B′=12 cm,B′C′=18 cm,A′C′=24 cm,此时,,,∴,∴△ABC∽△A′B′C′.
书写格式:在△ABC与△A′B′C′中,∵,∴△ABC∽△A′B′C′.
判定定理3:如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似.如图27-14所示.
书写格式:在△ABC与△A′B′C′中,∵,∠A=∠A′,∴△ABC∽△A′B′C′.
判定定理4:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.
如图27—15所示,在△ABC与△A′B′C′中,∠A=∠A′,∠B=∠B′,求证△ABC~△A′B′C′.
证明:在△ABC的边AB上截取AD=A′B′,
过点D作DE∥BC交AC于点E,
∴△ADE≌△A′B′C′,且△ADE~△ABC,
∴△ABC∽△A′B′C′.
书写格式:在△ABC与△A′B′C′中,∵∠A=∠A′,
∠B=∠B′,∴△ABC~△A′B′C′.
规律方法小结 判定三角形相似的方法主要有以下几种:(1)定义;(2)平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似;(3)如果两个三角形的三组对应边的比相等,那么这两个三角形相似;(4)如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似;(5)如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似;(6)直角三角形被斜边上的高分成的两个直角三角形都与原三角形相似(此知识常用,但有时需要证明);(7)若两个直角三角形满足一个锐角对应相等,或两组直角边的比相等,则这两个直角三角形相似.
知识点6 相似三角形的性质
相似三角形对应角相等,对应边的比相等.
拓展 相似三角形的性质可用于有关角的计算、线段的计算以及三角形的周长和面积的计算等,还可以用于证明两角相等、两条线段相等.
规律方法小结 运用转化思想把要求证的线段间的关系逐步转化为易证的线段间的关系,即由未知向已知转化.当两个三角形相似,但又没有指明对应的情况时,应进行分类讨论.
课堂检测
基本概念题
1、所有的直角三角形都相似吗?所有的等腰直角三角形呢?为什么?
2、根据下列条件判定△ABC与△A′B′C′是否相似,并说明理由.
(1)∠A=120°,AB=7 cm,AC=14 cm,∠A′=120°,A′B′=3 cm,A′C′=6 cm; (2)AB=4 cm,BC=6 cm,AC=8 cm,A′B′=12 cm,B′C′=18 cm,A′C′=21 cm.
基础知识应用题
3、如图27-17所示,根据下列情况写出各组相似三角形的对应边的比例式.
(1)△ABC∽△ADE,其中DE∥BC;
(2)△OAB∽△OA′B′,其中A′B′∥AB;
(3)△ABC∽△ADE,其中∠ADE=∠B.
4、如图27-18所示,已知AB∥CD∥EF,那么下列结论正确的是 ( )
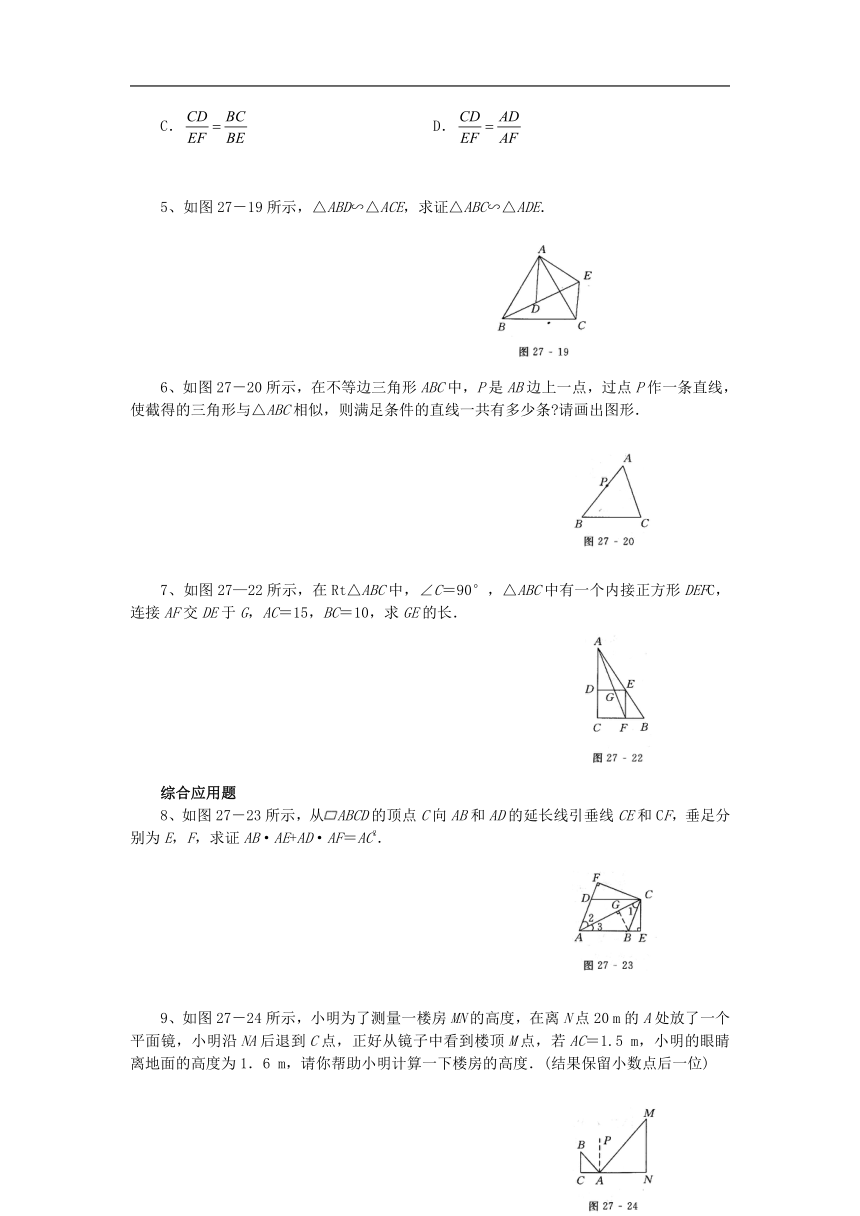
A. B.
C. D.
5、如图27-19所示,△ABD∽△ACE,求证△ABC∽△ADE.
6、如图27-20所示,在不等边三角形ABC中,P是AB边上一点,过点P作一条直线,使截得的三角形与△ABC相似,则满足条件的直线一共有多少条?请画出图形.
7、如图27—22所示,在Rt△ABC中,∠C=90°,△ABC中有一个内接正方形DEFC,连接AF交DE于G,AC=15,BC=10,求GE的长.
综合应用题
8、如图27-23所示,从ABCD的顶点C向AB和AD的延长线引垂线CE和CF,垂足分别为E,F,求证AB·AE+AD·AF=AC2.
9、如图27-24所示,小明为了测量一楼房MN的高度,在离N点20 m的A处放了一个平面镜,小明沿NA后退到C点,正好从镜子中看到楼顶M点,若AC=1.5 m,小明的眼睛离地面的高度为1.6 m,请你帮助小明计算一下楼房的高度.(结果保留小数点后一位)
探索与创新题
10、如图27—25所示,在直角梯形ABCD中,∠D=90°,AD=7,AB=2,DC=3,P为AD上一点,以P,A,B为顶点的三角形与以P,D,C为顶点的三角形相似,那么这样的点P一共有多少个?为什么?
体验中考
1、如图27-28所示,已知△ABC是边长为6 cm的等边三角形,动点P,Q同时从A,B两点出发,分别沿AB,BC匀速运动,其中点P运动的速度是1 cm/s,点Q运动的速度是2 cm/s,当点Q到达点C时,P,Q两点都停止运动,设运动时间为t s,解答下列问题.
(1)当t=2时,判断△BPQ的形状,并说明理由;
(2)设△BPQ的面积为S cm2,求S与t的函数关系式;
(3)作QR∥BA交AC于点P,连接PR,当t为何值时,△APR∽△PRQ?
2、如图27-29所示,在ABCD中,E在DC上,若DE:EC=1:2,则BF:BE= .
学后反思
附: 课堂检测及体验中考答案
课堂检测
1、分析 由相似三角形的定义可知,所有的直角三角形不都相似,而所有的等腰直角三角形都相似.
解:所有的直角三角形不都相似.如图27—16所示的两个直角三角形中的两个
锐角显然不相等,因此这两个直角三角形不相似.
所有的等腰直角三角形都相似.因为任意一个等腰直角三角形的三个内角分别为45°,45°,90°,三条边的比为1:1:,因此所有的等腰直角三角形都相似.
【解题策略】 所有的直角三角形中不满足对应角都相等,因此所有的直角三角形不都相似.
2、分析 根据判断两个三角形相似的判定定理3与判定定理2来判定.
解:(1)∵,,∴.
又∵∠A=∠A′,∴△ABC∽△A′B′C′.
(2) , ,,∴.
即△ABC与△A′B′C′的三组对应边的比不相等,所以它们不相似.
【解题策略】 此类题主要考查相似三角形的判定定理.
3、分析 要写出比例式,关键应明确哪些边是对应边,而要找到对应边,比较好的方法是找到对应角(或对应的顶点).以(2)为例,由于A′B′∥AB,∴∠A=∠A′,∠B=∠B′,∠A′OB′=∠AOB,因此点A与点A′是对应点,点B与点B′是对应点,另一个公共点O是两个三角形的对应点.
解:(1)
(2) .
(3)
【解题策略】 两个三角形相似,在找对应角和对应边时应按照对应字母来找.
4、分析 如图27-18所示,把直线AD向右平移,且使点A与点B重合.容易证明:AD=BD′,DF=D′F′,由比例线段的特点知.故选A.
5、分析 由于△ABD∽△ACE,所以∠BAD=∠CAE,所以
∠BAC=∠DAE.又,所以问题得证.
证明:∵△ABD∽△ACE,∴∠BAD=∠CAE,
∴∠BAD+∠DAC=∠CAE+∠DAC,
即∠BAC=∠DAE.
又∵△ABD∽△ACE,∴,
即,∴△ABC∽△ADE.
【解题策略】 解决此类问题的关键是熟练掌握相似三角形的判定方法.
6、分析 可利用“如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似”和“平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似”来画直线,故过点P分别作BC,AC的平行线,或过点P作与∠C相等的角,从而得到相似三角形.
解:满足条件的直线一共有四条,如图27-21所示.
【解题策略】 本题考查相似三角形的识别方法,通过构造“两角对应相等”使两个三角形相似.
7、分析 根据相似三角形的判定方法和性质列出比例式,从而求得GE的长.
解:∵在Rt△ABC中,∠C=90°,正方形DEFC为其内接正方形,
∴△ADE∽△ACB,△AGE∽△AFB,
∴.
设正方形DEFC的边长为x,
则,∴x=6.
∵△AGE∽△AFB,∴.
又∵,∴,
即,∴GE=.
【解题策略】 利用比例式求线段的长度是求线段的一种重要方法,主要是根据相似的关系列出比例式,再由比例式列出方程,从而通过解方程求得线段的长.
8、分析 等式左边的两项均为两条线段之积,而右边为AC2,故应设法将AC2拆成两条线段乘积的形式,由图中可知AC2=AC(AG+GC)=AC·AG+AC·GC,从而只需证AC·AG和AC·GC与所证等式的左端两项分别相等即可.
证明:过B作BG⊥AC于G,
∵∠BGA=∠CEA=90°,∠3=∠3,
∴△ABG∽△ACE,∴,
∴AC·AG=AB·AE.①
又∵BC∥AD,CF⊥AF,
∴∠1=∠2,∠CGB=∠AFC=90°,
∴△CBG∽△ACF,∴,
∴AC·CG=CB·AF.②
由①+②得AC(AG+CG)=AB·AE+CB·AF.
又∵CB=AD,∴AB·AE+AD·AF=AC2.
【解题策略】 一般地,要证形如ab=cd+ef的线段关系,常常在a(或b)上取一点P,使ab转化为两项.
9、分析 根据物理学中的反射定律可知:光线的反射角等于入射角,即∠BAP=∠MAP,从而∠BAC=∠MAN,这样就可以得到△MNA∽△BCA,再利用相似三角形的性质即可求出MN.
解:∵BC⊥CA,MN⊥AN,∴∠BCA=∠MNA=90°,
又∵∠BAP=∠MAP,∴∠BAC=∠MAN,
∴△BCA∽△MNA,∴MN:BC=AN:AC,
即MN:1.6=20:1.5,∴MN=≈21.3(m),
∴楼房的高度约为21.3 m.
【解题策略】 利用相似三角形的对应边成比例,列出比例式求线段的长是常用的方法.
10、分析 △PAB与△PDC中各有一个直角,两边对应成比例,所以应分两种情况进行讨论,即∠APB=∠DPC和∠APB=∠PCD,分别求解即可.
解:设AP=x,则PD=7-x.
①当△PAB∽△PDC,即∠A=∠D=90°,∠APB=∠DPC时,
,∴x=.
②当△PAB∽△CDP,即∠A=∠D=90°,∠APB=∠DCP时,
,∴x1=1,x2=6.
因此AP的值有三个,也就是这样的点P一共有三个.
【解题策略】 本题中△PAB与△PDC相似,由于没有指明两个三角形的对应点(除点A和点D外),所以要分类讨论.
体验中考
1、分析 (1)∠B=60°,只要判断出BQ与BP的关系即可.(2)用含t的代数式分别表示BP和BP边上的高,因此需过点Q作BP边上的高;(3)找出使△APR∽△PRQ成立的条件即可.
解:(1)△BPQ是等边三角形,理由如下:
当t=2时,AP=2×1=2,BQ=2×2=4,
∴BP=AB-AP=6-2=4 .
∴BQ=BP.
又∵∠B=60°,
∴△BPQ是等边三角形.
(2)过点Q作QE⊥AB,垂足为点E.
由QB=2t,得QE=2t·sin 60°=t.
由AP=t,得PB=6-t.
∴S△BPQ=BP·QE=(6-t)×t=-t2+3t.
(3)∵QR∥BA,
∴∠QRC=∠A=60°,∠RQC=∠B=60°.
又∵∠C=60°,
∴△QRC是等边三角形,
∴QR=RC=QC=6-2t.
∵BE=BQ·cos 60°=2t×=t,
∴EP=AB-AP-BE=6-t-t=6-2t.
∴EP=QR,
又∵EP∥QR,∴四边形EPRQ是平行四边形,
∴PR=EQ=t.
又∵∠PEQ=90°,∴∠APR=∠PRQ=90°.
∵△APR∽△PRQ,∴∠QPR=∠A=60°.
∴tan 60°=,即=,解得t=.
∴当t=s时,△APR∽△PRQ.
【解题策略】 分析动点问题时,要抓住动点的起点、运动方向、速度、时间、距离等要素.
2、分析 ∵DE:EC=1:2,∴设DE=x,则EC=2x,∴AB=3x.由△ABF∽△CEF,得∴BF:BE=3:5.故填3:5.
相似三角形
相似三角形的判定
