人教A版数学必修2第二章 点、直线、平面之间的位置关系2.3 直线、平面垂直的判定及其性质 (课件16张PPT)
文档属性
| 名称 | 人教A版数学必修2第二章 点、直线、平面之间的位置关系2.3 直线、平面垂直的判定及其性质 (课件16张PPT) | 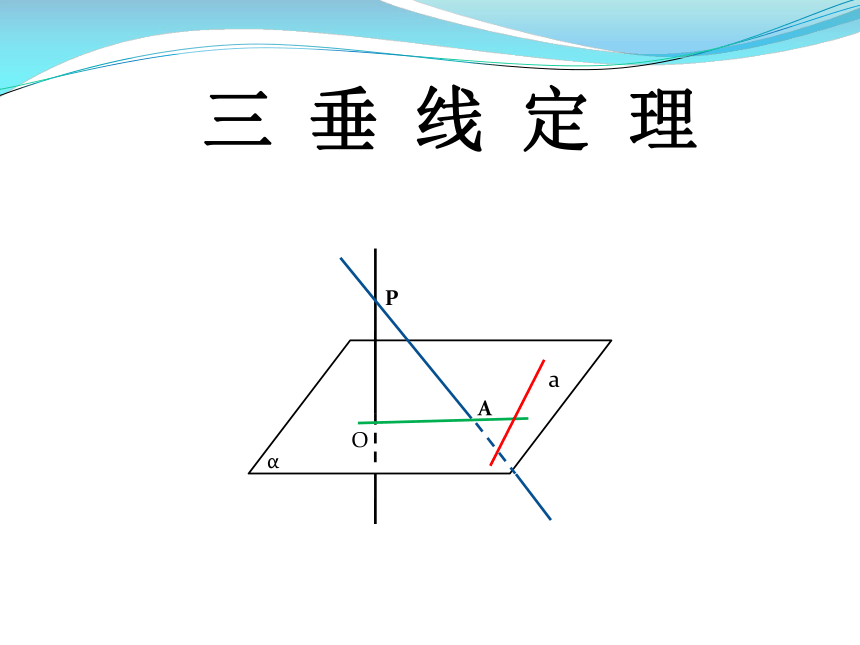 | |
| 格式 | zip | ||
| 文件大小 | 411.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-10 21:55:11 | ||
图片预览



文档简介
(共16张PPT)
三 垂 线 定 理
P
O
A
α
a
直线和平面垂直的判定定理是什么?
直线和平面垂直的定义是什么?有怎样的性质?
定义:一条直线和平面相交,且和平面内经过交点的所有直线都垂直
性质定理:如果一条直线和平面垂直,那么它垂直于平面内的任何直线
判定定理:如果平面外一条直线和平面内两条相交直线都垂直,那么这条直线垂直于平面
P
O
A
α
如图:请说出下列图形中的垂线、斜线和射影。
直线PA是斜线
直线PO是垂线
直线OA是直线PA在平面内的射影
a
思考:
若 ,直线a和直线PA是什么关系?
P
O
A
α
a
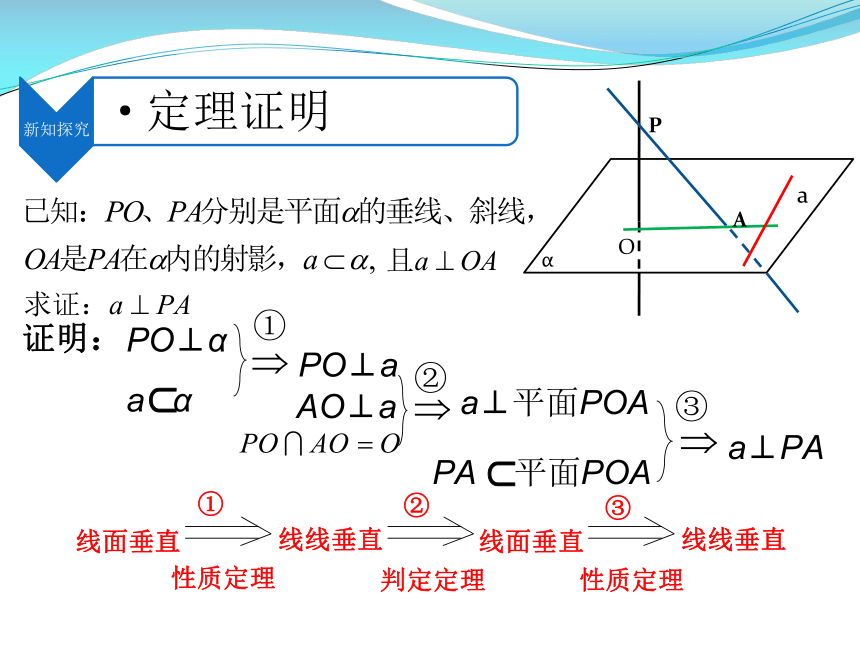
PO⊥α
a α
∪
①
PO⊥a
PA 平面POA
∪
a⊥PA
③
证明:
③
线线垂直
②
线面垂直
线面垂直
①
线线垂直
性质定理
判定定理
性质定理
AO⊥a
②
a⊥平面POA
P
O
A
α
a
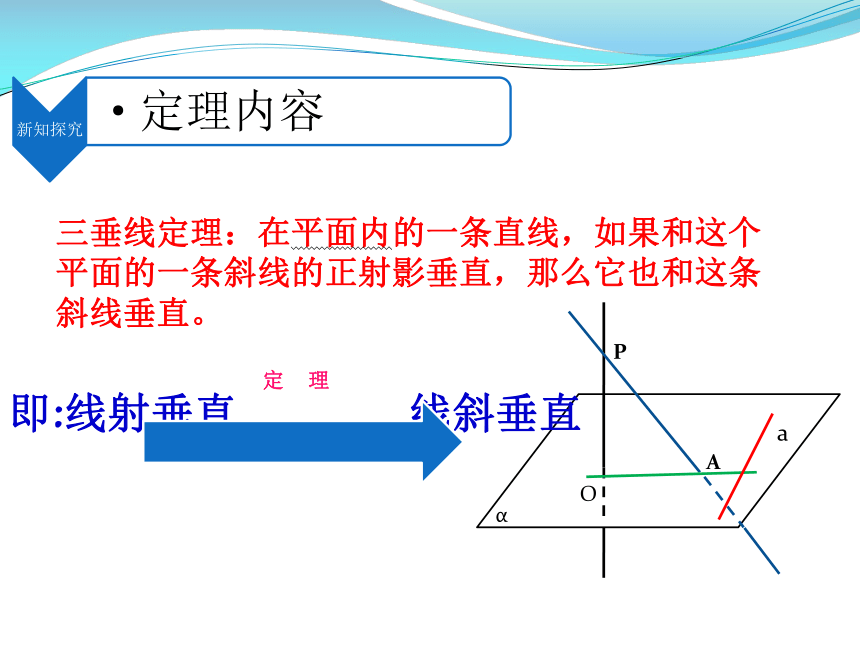
三垂线定理:在平面内的一条直线,如果和这个平面的一条斜线的正射影垂直,那么它也和这条斜线垂直。
即:线射垂直 线斜垂直
定 理
P
O
A
a
α
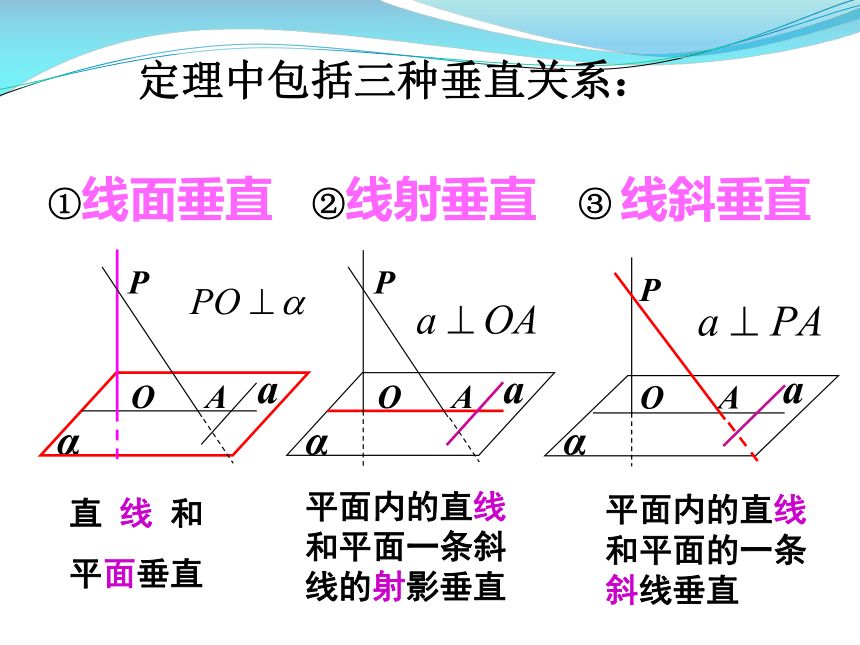
定理中包括三种垂直关系:
②线射垂直
P
O
A
a
α
①线面垂直
③ 线斜垂直
P
O
A
a
α
直 线 和
平面垂直
平面内的直线和平面一条斜线的射影垂直
平面内的直线和平面的一条斜线垂直
P
O
A
α
a
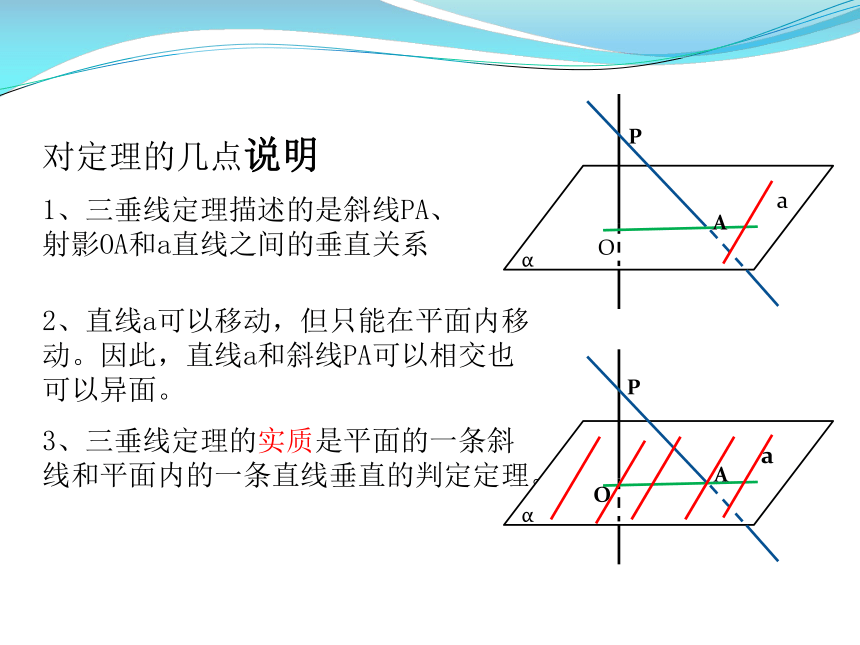
对定理的几点说明
1、三垂线定理描述的是斜线PA、射影OA和a直线之间的垂直关系
2、直线a可以移动,但只能在平面内移动。因此,直线a和斜线PA可以相交也可以异面。
3、三垂线定理的实质是平面的一条斜线和平面内的一条直线垂直的判定定理。
α
a
P
O
A
思考:
如果将定理中的条件a⊥OA改成a⊥PA,你会得到怎样的结果?命题一定成立吗?
P
O
A
α
a
线射垂直
逆定理
定 理
线斜垂直
线斜垂直
线射垂直
逆定理
结论:a⊥OA
A
B
C
D
O
A1
D1
C1
B1
例1:如图,在正方体中,O是AC与BD的交点,直线D1O与AC垂直吗?说明你的理由。
D1O在平面ABCD内的射影是DO
AC与BD垂直
D1O与AC垂直( )
三垂线定理
你知道吗? D1B⊥AC
线射垂直 线斜垂直
例2、道旁有一条河,彼岸有电塔AB,高15m,只有测角
器和皮尺作测量工具,能否求出电塔顶与道路的距离?
解:在道边取一点C,
使BC与道边所成水平角等于90°,
再在道边取一点D,
使水平角CDB等于45°,
测得C、D的距离等于20m
B
A
C
90°
D
⌒
45°
应用举例
B
A
C
90°
D
⌒
45°
∵BC是AC的射影 且CD⊥BC ∴CD⊥AC(三垂线定理)
∵∠CDB=45°,CD⊥BC,CD=20m ∴BC=20m,
在直角三角形ABC中
AC2=AB2+BC2,AC= 152+202 =25(m)
答:电塔顶与道路的距离是25m。
因此斜线AC的长度就是电塔顶与道路的距离。
应用举例
“一垂二射三证”
P
O
A
α
a
线射垂直
逆定理
定 理
线斜垂直
三垂线定理及三垂线定理逆定理
定理和逆定理是证明线线垂直的重要方法!
如图:已知点P是ΔABC所在平面外一点,若点P在平面内的射影O恰好是ΔABC的垂心,求证:PA⊥BC(教材练习题)
P
O
A
C
B
垂心:三边高的交点
“问百度”
三角形的外心、内心、重心、垂心,并摘抄!
再见
感谢您的莅临指导
三 垂 线 定 理
P
O
A
α
a
直线和平面垂直的判定定理是什么?
直线和平面垂直的定义是什么?有怎样的性质?
定义:一条直线和平面相交,且和平面内经过交点的所有直线都垂直
性质定理:如果一条直线和平面垂直,那么它垂直于平面内的任何直线
判定定理:如果平面外一条直线和平面内两条相交直线都垂直,那么这条直线垂直于平面
P
O
A
α
如图:请说出下列图形中的垂线、斜线和射影。
直线PA是斜线
直线PO是垂线
直线OA是直线PA在平面内的射影
a
思考:
若 ,直线a和直线PA是什么关系?
P
O
A
α
a
PO⊥α
a α
∪
①
PO⊥a
PA 平面POA
∪
a⊥PA
③
证明:
③
线线垂直
②
线面垂直
线面垂直
①
线线垂直
性质定理
判定定理
性质定理
AO⊥a
②
a⊥平面POA
P
O
A
α
a
三垂线定理:在平面内的一条直线,如果和这个平面的一条斜线的正射影垂直,那么它也和这条斜线垂直。
即:线射垂直 线斜垂直
定 理
P
O
A
a
α
定理中包括三种垂直关系:
②线射垂直
P
O
A
a
α
①线面垂直
③ 线斜垂直
P
O
A
a
α
直 线 和
平面垂直
平面内的直线和平面一条斜线的射影垂直
平面内的直线和平面的一条斜线垂直
P
O
A
α
a
对定理的几点说明
1、三垂线定理描述的是斜线PA、射影OA和a直线之间的垂直关系
2、直线a可以移动,但只能在平面内移动。因此,直线a和斜线PA可以相交也可以异面。
3、三垂线定理的实质是平面的一条斜线和平面内的一条直线垂直的判定定理。
α
a
P
O
A
思考:
如果将定理中的条件a⊥OA改成a⊥PA,你会得到怎样的结果?命题一定成立吗?
P
O
A
α
a
线射垂直
逆定理
定 理
线斜垂直
线斜垂直
线射垂直
逆定理
结论:a⊥OA
A
B
C
D
O
A1
D1
C1
B1
例1:如图,在正方体中,O是AC与BD的交点,直线D1O与AC垂直吗?说明你的理由。
D1O在平面ABCD内的射影是DO
AC与BD垂直
D1O与AC垂直( )
三垂线定理
你知道吗? D1B⊥AC
线射垂直 线斜垂直
例2、道旁有一条河,彼岸有电塔AB,高15m,只有测角
器和皮尺作测量工具,能否求出电塔顶与道路的距离?
解:在道边取一点C,
使BC与道边所成水平角等于90°,
再在道边取一点D,
使水平角CDB等于45°,
测得C、D的距离等于20m
B
A
C
90°
D
⌒
45°
应用举例
B
A
C
90°
D
⌒
45°
∵BC是AC的射影 且CD⊥BC ∴CD⊥AC(三垂线定理)
∵∠CDB=45°,CD⊥BC,CD=20m ∴BC=20m,
在直角三角形ABC中
AC2=AB2+BC2,AC= 152+202 =25(m)
答:电塔顶与道路的距离是25m。
因此斜线AC的长度就是电塔顶与道路的距离。
应用举例
“一垂二射三证”
P
O
A
α
a
线射垂直
逆定理
定 理
线斜垂直
三垂线定理及三垂线定理逆定理
定理和逆定理是证明线线垂直的重要方法!
如图:已知点P是ΔABC所在平面外一点,若点P在平面内的射影O恰好是ΔABC的垂心,求证:PA⊥BC(教材练习题)
P
O
A
C
B
垂心:三边高的交点
“问百度”
三角形的外心、内心、重心、垂心,并摘抄!
再见
感谢您的莅临指导
