人教A版数学必修1第二章 基本初等函数2.2.1对数与对数运算(2) (18张PPT)
文档属性
| 名称 | 人教A版数学必修1第二章 基本初等函数2.2.1对数与对数运算(2) (18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 237.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-10 22:04:38 | ||
图片预览






文档简介
(共18张PPT)
2.2.1对数与对数运算
第二课时 对数的运算性质
学习目标
1、理解并掌握对数的运算性质,了解对数运算法则的推导方法;
2、能初步运用对数的运算性质进行化简、求值.
重难点:对数运算性质的推导与应用.
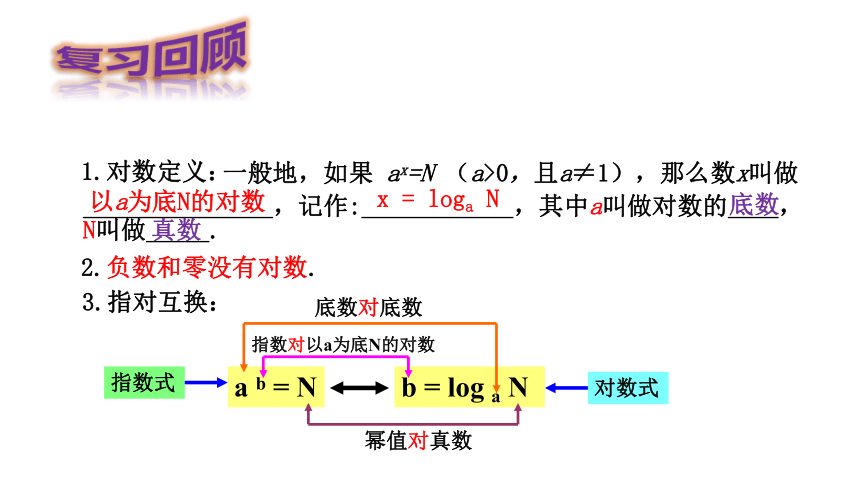
复习回顾
1.对数定义:
一般地,如果 ax=N (a>0,且a≠1),那么数x叫做
,记作: ,其中a叫做对数的 ,N叫做 .
以a为底N的对数
x = loga N
底数
真数
a b = N
b = log a N
指数式
对数式
底数对底数
幂值对真数
3.指对互换:
指数对以a为底N的对数
2.负数和零没有对数.
复习回顾
4.对数恒等式:
5.重要结论:(1)log a a = ;(2)log a 1 =
6.指数的部分运算性质:
1
0
温故知新
问题:我们之前已经学习了指数的运算性质,也知道指数与对数有着密切的联系,那么我们就会去思考,对数有哪些运算性质呢?
我们该如何证明这些结论呢?
探索新知
简记为:“积的对数=对数的和”
探索新知
简记为:“商的对数=对数的差”
探索新知
证明:设
由对数的定义可以得:
∴
即证得
能否令等式左边为 呢?
探索新知
例1、计算:
还可以先算
括号里面的
乘方
注意:有时要逆向运用公式
探索新知
练习1、计算:
(1)
(3)
(2)
注意:有时要逆向运用公式
探索新知
例2、
解(1)
解(2)
用
表示下列各式:
探索新知
练习2、 用lgx,lgy,lgz表示下列各式:
(1)
(2)
=lgx+lgy+lgz;
探索新知
例3、
为什么没有先把 提出来?
随堂演练
1、计算:
2、计算:
随堂演练
1、计算:
解法一:
解法二:
解:原式
解:原式
合
分
随堂演练
解:原式
2、计算:
课堂小结
积、商、幂的对数运算法则:
如果 a > 0,a ? 1,M > 0, N > 0 有:
有时要逆向运用公式
课后作业
1、教材:
P68练习:第2、3题;
P74习题:第3、4、5题.
2、点金:
P49课内巩固 基础训练:全部.
思考题:已知 , ,求 的值.
2.2.1对数与对数运算
第二课时 对数的运算性质
学习目标
1、理解并掌握对数的运算性质,了解对数运算法则的推导方法;
2、能初步运用对数的运算性质进行化简、求值.
重难点:对数运算性质的推导与应用.
复习回顾
1.对数定义:
一般地,如果 ax=N (a>0,且a≠1),那么数x叫做
,记作: ,其中a叫做对数的 ,N叫做 .
以a为底N的对数
x = loga N
底数
真数
a b = N
b = log a N
指数式
对数式
底数对底数
幂值对真数
3.指对互换:
指数对以a为底N的对数
2.负数和零没有对数.
复习回顾
4.对数恒等式:
5.重要结论:(1)log a a = ;(2)log a 1 =
6.指数的部分运算性质:
1
0
温故知新
问题:我们之前已经学习了指数的运算性质,也知道指数与对数有着密切的联系,那么我们就会去思考,对数有哪些运算性质呢?
我们该如何证明这些结论呢?
探索新知
简记为:“积的对数=对数的和”
探索新知
简记为:“商的对数=对数的差”
探索新知
证明:设
由对数的定义可以得:
∴
即证得
能否令等式左边为 呢?
探索新知
例1、计算:
还可以先算
括号里面的
乘方
注意:有时要逆向运用公式
探索新知
练习1、计算:
(1)
(3)
(2)
注意:有时要逆向运用公式
探索新知
例2、
解(1)
解(2)
用
表示下列各式:
探索新知
练习2、 用lgx,lgy,lgz表示下列各式:
(1)
(2)
=lgx+lgy+lgz;
探索新知
例3、
为什么没有先把 提出来?
随堂演练
1、计算:
2、计算:
随堂演练
1、计算:
解法一:
解法二:
解:原式
解:原式
合
分
随堂演练
解:原式
2、计算:
课堂小结
积、商、幂的对数运算法则:
如果 a > 0,a ? 1,M > 0, N > 0 有:
有时要逆向运用公式
课后作业
1、教材:
P68练习:第2、3题;
P74习题:第3、4、5题.
2、点金:
P49课内巩固 基础训练:全部.
思考题:已知 , ,求 的值.
