沪教版(五四学制)七年级上册:9.7 同底数幂的乘法 课件(26张PPT)
文档属性
| 名称 | 沪教版(五四学制)七年级上册:9.7 同底数幂的乘法 课件(26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 215.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-05 17:03:26 | ||
图片预览






文档简介
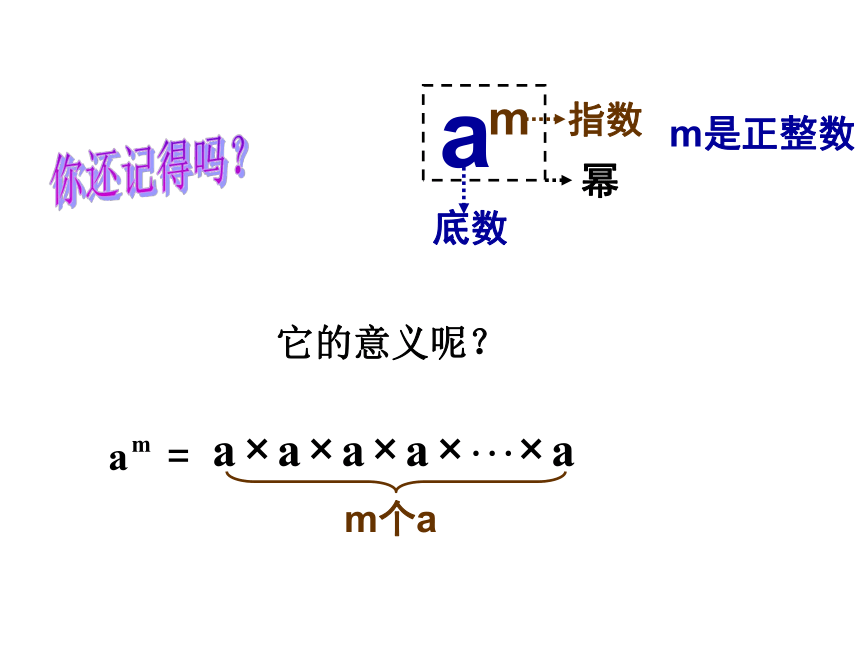
课件26张PPT。七年级第一学期数学9.7同底数幂的乘法底数指数幂m是正整数你还记得吗?它的意义呢?m个a* 负数与分数作底数时要打上括号。那么我们如何计算呢?根据乘方的意义:2个105个107个10以2为底的幂试一试:(1)×(2)×(3)×猜一猜:×786m+n以2为底的幂 我们观察上述各等式可以 发现,等式左边 的这两个因数底数相同,是同底的幂的形式
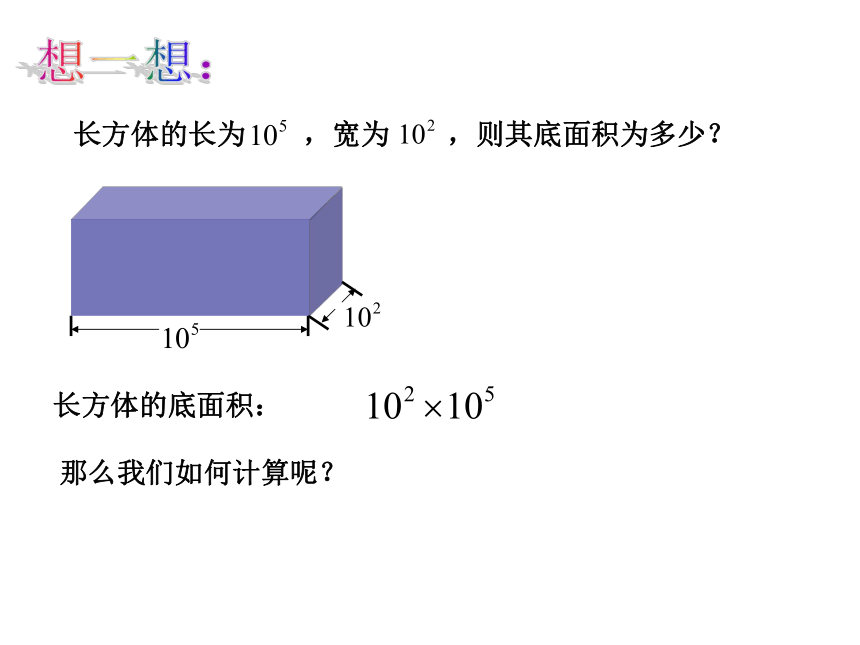
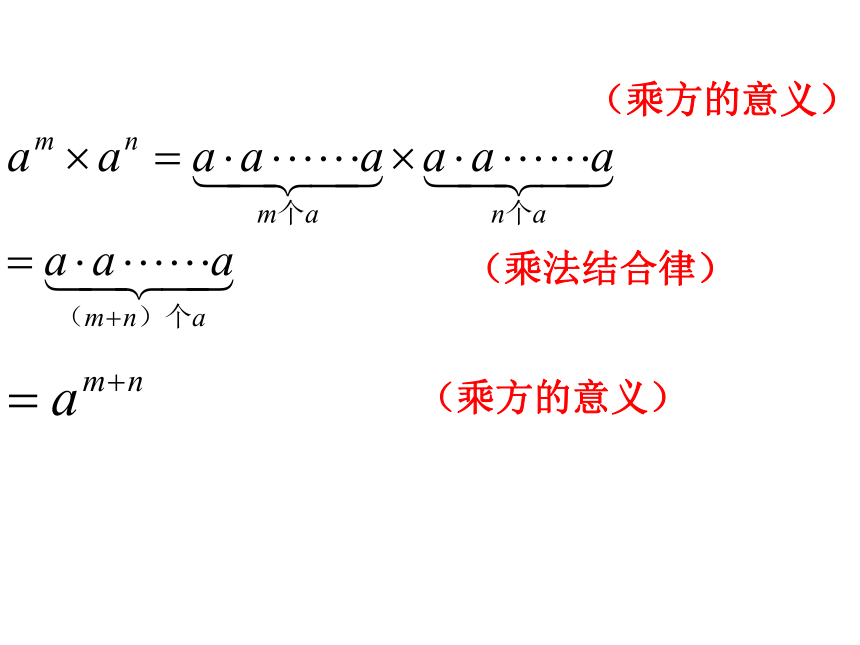
所以我们上述这种运算叫做同底数幂的乘法我们如何说明这个等式是否成立呢?请试一试同底数幂的乘法(乘方的意义)(乘法结合律)(乘方的意义)由此,我们可以得到:(m、n是正整数)长方体的长为 ,宽为 ,则其底面积为多少?想一想:如果有多个同底数幂相乘,底数仍不变,指数仍相加(m、n、p是正整数) 练习一
1.???计算下列各式,结果用幂的形式表示(2) (3) (x+y)5 ·(y+x)6 (4) (a-b)4 ·(b-a)3 (1) 105×106 (5) (-a)3 ·(-a2)·a4· a (6) (2m-n)2t+1 ·(n-2m)4t+2· (2m-n) 练习二
2、下面的计算对不对?如果不对,怎样改正?
(1)b5 · b5= 2b5 ( ) (2)b5 + b5 = b10 ( )
(3)x5 ·x5 = x25 ( ) (4)y5 · y5 = 2y10 ( )
(5)c · c3 = c3 ( ) (6)m + m3 = m4 ( )
m + m3 = m + m3 b5 · b5= b10 b5 + b5 = 2b5 x5 · x5 = x10 y5 · y5 =y10 c · c3 = c4× × × ×××例1 计算:(1)(2)(3)(4)(5)y4·y3·y2·y例2 计算:(1)(2)(3)例3 计算:(1)?????? x5·x3 – x4·x4 + x7·x + x6x2
(2)?????? y2·ym–2 + y·ym–1 – y3·ym
解:(1)原式 = x8 – x8 + x8 + x8 = 2x8
(2)原式 = ym + ym – ym+3 = 2ym – ym+3 变式训练:1、填空:
(1)x5 ·( )= x 8 (2)a ·( )= -a6
(3)x · x3( )= x7 (4)xm ·( )=x3m
x3(-a)5 x3x2m2、填空:
(1) 8 = 2x,则 x = ;
(2) 8× 4 = 2x,则 x = ;
(3) 3×27×9 = 3x,则 x = 。35623 23 3253622 × = 33 32 × ×= 练习三
3.???计算:∵am · an = am+n (m、n为正整数)∴ am+n = am · an (m、n为正整数)已知:am=2, an=3.
求am+n =?.动脑筋解: am+n = am · an
=2 × 3=6 试一试:解一:解二:由题意得 x + 3 = 5,解得x = 2拓展训练,深化提高 填空:
(1)如果an–3·a2n+1 = a10,
则 n = ____________________;
(2)已知 2×8n×16n = 222,
则 n = ______________________;
(3) an+1·am+n = a6且m – 2n = 1,
则 mn = ______________________。
334例4 已知 (x + y)2 = 2,(x - y)3 = 3
求:(x + y)7 (x - y)2 (y + x)3 (y - x)4 解:原式 =(x + y)7 (x - y)2 (x + y)3 (x - y)4 =(x + y)10 (x - y)6 =[(x + y)2]5 [(x - y)3]2 当(x + y)2=2,(x - y)3=3时 原式 =25 ×32 =288课时小结am+n = am · an (m、n为正整数)am · an = am+n (m、n为正整数)* 公式中的a可以是数也可以是式子;
* 公式中的指数可以增加,法则仍然成立;
* – a2与(– a)2的区别;
* 底数互为相反数的可先化成同底数幂再计算;
(– a)2n = a2n;(x + y)n=(y +x)n
(– a)2n+1 = – a2n+1 ; (x – y)2n-1 = –(y – x)2n-1
* 同底数幂乘法法则可以逆用。
所以我们上述这种运算叫做同底数幂的乘法我们如何说明这个等式是否成立呢?请试一试同底数幂的乘法(乘方的意义)(乘法结合律)(乘方的意义)由此,我们可以得到:(m、n是正整数)长方体的长为 ,宽为 ,则其底面积为多少?想一想:如果有多个同底数幂相乘,底数仍不变,指数仍相加(m、n、p是正整数) 练习一
1.???计算下列各式,结果用幂的形式表示(2) (3) (x+y)5 ·(y+x)6 (4) (a-b)4 ·(b-a)3 (1) 105×106 (5) (-a)3 ·(-a2)·a4· a (6) (2m-n)2t+1 ·(n-2m)4t+2· (2m-n) 练习二
2、下面的计算对不对?如果不对,怎样改正?
(1)b5 · b5= 2b5 ( ) (2)b5 + b5 = b10 ( )
(3)x5 ·x5 = x25 ( ) (4)y5 · y5 = 2y10 ( )
(5)c · c3 = c3 ( ) (6)m + m3 = m4 ( )
m + m3 = m + m3 b5 · b5= b10 b5 + b5 = 2b5 x5 · x5 = x10 y5 · y5 =y10 c · c3 = c4× × × ×××例1 计算:(1)(2)(3)(4)(5)y4·y3·y2·y例2 计算:(1)(2)(3)例3 计算:(1)?????? x5·x3 – x4·x4 + x7·x + x6x2
(2)?????? y2·ym–2 + y·ym–1 – y3·ym
解:(1)原式 = x8 – x8 + x8 + x8 = 2x8
(2)原式 = ym + ym – ym+3 = 2ym – ym+3 变式训练:1、填空:
(1)x5 ·( )= x 8 (2)a ·( )= -a6
(3)x · x3( )= x7 (4)xm ·( )=x3m
x3(-a)5 x3x2m2、填空:
(1) 8 = 2x,则 x = ;
(2) 8× 4 = 2x,则 x = ;
(3) 3×27×9 = 3x,则 x = 。35623 23 3253622 × = 33 32 × ×= 练习三
3.???计算:∵am · an = am+n (m、n为正整数)∴ am+n = am · an (m、n为正整数)已知:am=2, an=3.
求am+n =?.动脑筋解: am+n = am · an
=2 × 3=6 试一试:解一:解二:由题意得 x + 3 = 5,解得x = 2拓展训练,深化提高 填空:
(1)如果an–3·a2n+1 = a10,
则 n = ____________________;
(2)已知 2×8n×16n = 222,
则 n = ______________________;
(3) an+1·am+n = a6且m – 2n = 1,
则 mn = ______________________。
334例4 已知 (x + y)2 = 2,(x - y)3 = 3
求:(x + y)7 (x - y)2 (y + x)3 (y - x)4 解:原式 =(x + y)7 (x - y)2 (x + y)3 (x - y)4 =(x + y)10 (x - y)6 =[(x + y)2]5 [(x - y)3]2 当(x + y)2=2,(x - y)3=3时 原式 =25 ×32 =288课时小结am+n = am · an (m、n为正整数)am · an = am+n (m、n为正整数)* 公式中的a可以是数也可以是式子;
* 公式中的指数可以增加,法则仍然成立;
* – a2与(– a)2的区别;
* 底数互为相反数的可先化成同底数幂再计算;
(– a)2n = a2n;(x + y)n=(y +x)n
(– a)2n+1 = – a2n+1 ; (x – y)2n-1 = –(y – x)2n-1
* 同底数幂乘法法则可以逆用。
