人教A版数学必修3第一章 算法初步1.3 算法案例 (课件32张PPT)
文档属性
| 名称 | 人教A版数学必修3第一章 算法初步1.3 算法案例 (课件32张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 268.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-11 07:07:35 | ||
图片预览










文档简介
(共32张PPT)
1.3 算法案例
第2课时 秦九韶算法与进位制
2019.11
课程标准 学习要求 数学素养
通过阅读中国古代数学中的算法案例,体会中国古代数学对世界数学发展的贡献 1.了解算法的含义,体会算法的思想
2.在分析案例的基础上了解算法的基本特征
3.理解秦九韶算法的计算过程,并了解它提高计算效率的实质.
4理解进位制的概念,能进行不同进位制间的转化.
数学抽象
数学运算
逻辑推理
课堂探究
思考1 按我们平时的求解方法,把x的值代入多项式,计算各项
的值,然后相加共做了多少乘法、加法次运算?
阅读课本P37~38页
探究一:怎样求多项式 时的值呢?
答案 4+3+2+1=10次乘法运算,5次加法运算
思考2 如果我们先计算 ,然后再依次计算
的值,然后相加共做了多少乘法、加法次运算?
答案 4次乘法运算,5次加法运算
课堂探究
比较上述两种方法,第二种乘法运算次数减少了,因而能提高运算效率,对计算机来说,做一次乘法运算所用时间比作一次加法运算要长得多,所以采用第二种做法,计算机能更快得到结果。这就是我国南宋时期的数学家秦九韶在《数书九章》中提出的算法----秦九韶算法
探究一:怎样求多项式 时的值呢?
课堂探究
探究二:秦九韶算法及其应用
思考3 衡量一个算法是否优秀的重要参数是速度.把多项式f(x)=x5+x4+x3+x2+x+1变形为f(x)=((((x+1)x+1)x+1)x+1)x+1,然后求当x=5时的值,为什么比常规逐项计算省时?
答案 从里往外计算,充分利用已有成果,可减少重复计算.
探究一:怎样求多项式 时的值呢?
解:根据秦九韶算法,把多项式改写成如下形式:
按照从内到外的顺序,依次计算一次多项式当x=5时的值:
所以当x=5时,多项式的值为3906
思考4:利用后一种算法求多项式f(x)=anxn+an-1xn-1
+…+a1x+a0的值,这个多项式应写成哪种形式?
f(x)=anxn+an-1xn-1+…+a1x+a0
=(anxn-1+an-1xn-2+…+a2x+a1)x+a0
=((anxn-2+an-1xn-3+…+a2)x+a1)x+a0 =…
=(…((anx+an-1)x+an-2)x+…+a1)x+a0.
思考5:对于f(x)=(…((anx+an-1)x+ an-2)x+…+a1)x+a0,由内向外逐层计算一次多项式的值,其算法步骤如何?
第一步,计算v1=anx+an-1.
第二步,计算v2=v1x+an-2.
第三步,计算v3=v2x+an-3.
…
第n步,计算vn=vn-1x+a0.
思考6:上述求多项式f(x)=anxn+an-1xn-1+…+a1x+a0的值的方法称为秦九韶算法,利用该算法求f(x0)的值,一共需要多少次乘法运算,多少次加法运算?
思考7:在秦九韶算法中,记v0=an,那么第k步的算式是什么?
vk=vk-1x+an-k (k=1,2,…,n)
n次乘法,n次加法
秦九韶算法原理、程序框图及其相应程序
把一个n次多项式f(x)=anxn+an-1xn-1+…+a1x+a0改写成如下形式:(…((anx+an-1)x+an-2)x+…+a1)x+a0,求多项式的值时,首先计算
一次多项式的值,即v1= , 然后由内向外逐层计算一次多项式的值,即v2= ,
v3= ,…
vn= ,
这样,求n次多项式f(x)的值就转化为求 的值.
anx+an -1
最内层括号内
v1x+an-2
v2x+an-3
vn-1x+a0
n个一次多项式
秦九韶算法的原理
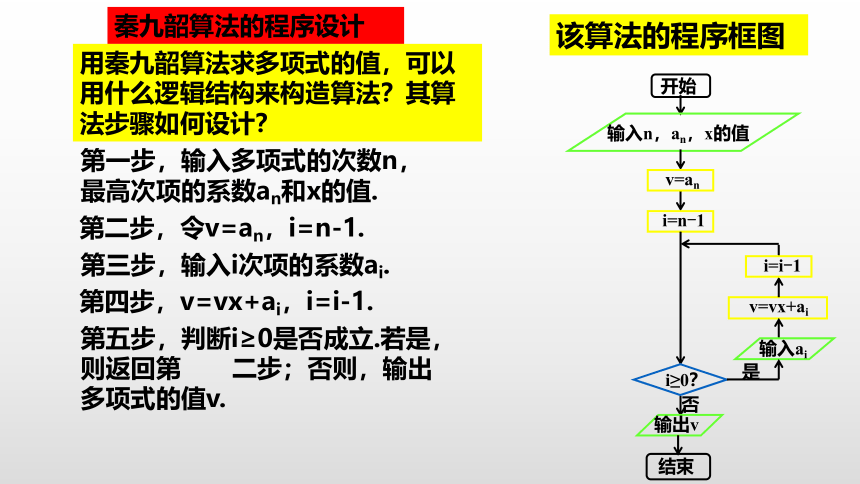
秦九韶算法的程序设计
用秦九韶算法求多项式的值,可以用什么逻辑结构来构造算法?其算法步骤如何设计?
第一步,输入多项式的次数n,最高次项的系数an和x的值.
第二步,令v=an,i=n-1.
第三步,输入i次项的系数ai.
第四步,v=vx+ai,i=i-1.
第五步,判断i≥0是否成立.若是,则返回第 二步;否则,输出多项式的值v.
该算法的程序框图
开始
输入n,an,x的值
v=an
v=vx+ai
输入ai
i=n-1
i=i-1
i≥0?
是
输出v
否
结束
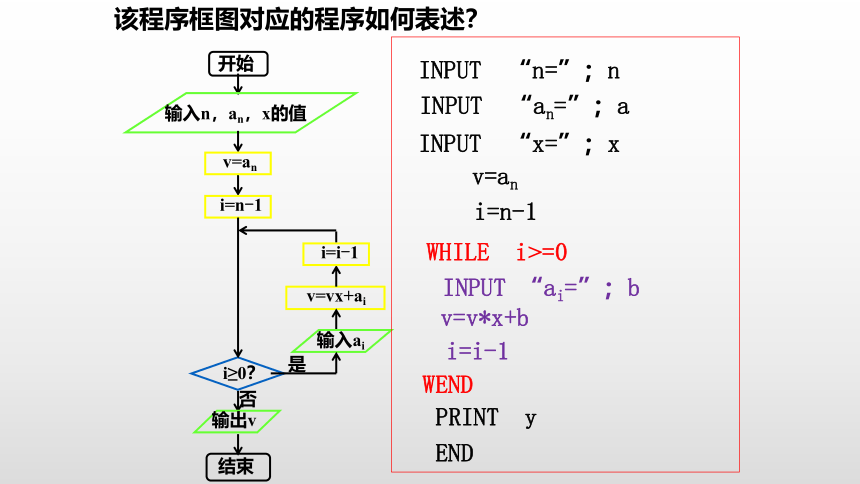
该程序框图对应的程序如何表述?
开始
输入n,an,x的值
v=an
v=vx+ai
输入ai
i≥0?
i=n-1
i=i-1
结束
是
输出v
否
INPUT “n=”;n
INPUT “an=”;a
INPUT “x=”;x
v=an
i=n-1
WHILE i>=0
INPUT “ai=”;b
v=v*x+b
i=i-1
WEND
PRINT y
END
例1:已知一个5次多项式 ,,用秦九韶算法求这个多项式当x=5时的值呢。
解:根据秦九韶算法,把多项式改写成如下形式:
按照从内到外的顺序,依次计算一次多项式当x=5时的值:
所以当x=5时,多项式的值为14130.2
例2 阅读下列程序,说明它解决的实际问题是什么?
INPUT “x=”;a
n=0
y=0
WHLE n<5
y=y+(n+1)*a?n
n=n+1
WEND
PRINT y
END
求多项式 在x=a时的值.
归纳小结
评价一个算法好坏的一个重要标志是运算的次数,如果一个算法从理论上需要超出计算机允许范围内的运算次数,那么这样的算法就只能是一个理论算法.在多项式求值的各种算法中,秦九韶算法是一个优秀算法.
作业:
P45练习:2.
P48习题1.3A组:2.
阅读课本P40~45页完成下列问题:
1.进位制的概念
位制是人们为了_____和_____方便而约定的记数系统,“满几进一”就是_____制,_____制的基数(基数都是大于1的整数)就是___.
常见的进位制有二进制,七进制(一周7天)、十进制(我们最熟悉的进位制),十二进制(一年12个月)及六十进制(一小时60分钟).
计数
几
几进
运算
几进制
2. k进制数的表示方法
一般地,若k是一个大于1的整数,那么以k为基数的k进制数可以表示为一串数字连写在一起的形式:anan-1an-2…a1a0(k)(an,an-1,…,a1,a0∈N,0<an<k,0≤an-1,…,a1,a0<k).
3. k进制数与10进制数的转化
①由k进制anan-1an-2…a1a0(k)转化为10进制数
anan-1an-2…a1a0(k)
=an×kn+an-1×kn-1+an-2×kn-2+…+a1×k+a0×k0;
②由10进制数转化为k进制数——除k取余法.
课堂探究:除k取余法
思考1:二进制数101101(2)化为十进制数是什么数?十进制数89化为二进制数是什么数?
101101(2)=25+23+22+1=45.
89=2×(2×(2×(2×(2×2+1)+1)+0)+0)+1
=1×26+0×25+1×24+1×23+0×22+0×21+1×20=1011001(2).
思考2:上述化十进制数为二进制数的算法叫做除2取余法,转化过程有些复杂,观察下面的算式你有什么发现吗?
2
1
2
2
2
5
0
2
11
2
22
2
44
2
89
1
0
0
1
1
0
1
余数
89=2×(2×(2×(2×(2×(2×(2×0+1)+0)+1)+1)+0)+0)+1
=2×(2×(2×(2×(22+0×21+1)+1)+0)+0)+1
=2×(2×(2×(23+0×22+1×21+1)+0)+0)+1
=…
=1×26+0×25+1×24+1×23+0×22+0×21+1×20
=101101(2)
思考3:上述方法也可以推广为把十进制数化为k进制数的算法,称为除k取余法,那么十进制数191化为五进制数是什么数?
0
5
1
5
7
5
38
5
191
1
3
2
1
余数
191=1231(5)
若十进制数 a除以2所得的商是q0,余数是r0, 即a=2×q0+ r0;
q0除以2所得的商是q1,余数是r1,即q0=2×q1+ r1;
……
qn-1除以2所得的商是0,余数是rn, 即qn-1= 2×0+rn,
那么十进制数a化为二进制数是什么数?
a=rnrn-1…r1r0(2)
思考4:
十进制化k进制的算法
思考1:根据上面的分析,将十进制数a化为二进制数的算法步骤如何设计?
第四步,若q≠0,则a=q,返回第二步;
否则,输出全部余数r排列得到的二进制数.
第一步,输入十进制数a的值.
第二步,求出a除以2所得的商q,余数r.
第三步,把所得的余数依次从右到左排列.
利用除k取余法,将十进制数a化为k进制数b的算法步骤如何设计?
第四步,若q≠0,则a=q,返回第二步;否则,输出全部余数r排列得到的k进制数.
第一步,输入十进制数a和基数k的值.
第二步,求出a除以k所得的商q,余数r.
第三步,把所得的余数依次从右到左排成一列.
将除k取余法的算法步骤用程序框图如何表示?
开始
输入a,k
求a除以k的商q
求a除以k的余数r
把所得的余数依次从右到左排成一列
a=q
q=0?
结束
输出全部余数r排列得到的k进制数
是
否
该程序框图对应的程序如何表述?
开始
输入a,k
求a除以k的商q
求a除以k的余数r
把所得的余数依次从右到左排列
a=q
q=0?
结束
输出全部余数r排
列得到的k进制数
是
否
INPUT “a,k=” a,k
b=0
i=0
DO
q=a\k
r=a MOD k
b=b+r*10∧i
i=i+1
a=q
LOOP UNTIL q=0
PRINT b
END
例1 将十进制数458分别转化为四进制数和六进制数.
0
4
1
4
7
4
28
4
114
4
458
2
2
0
3
1
余数
0
6
2
6
12
6
76
6
458
2
4
0
2
余数
458=13022(4)=2042(6)
例2 将五进制数3241(5)转化为七进制数.
30241(5)=3×54+2×52+4×5+1=1946.
0
7
5
7
39
7
278
7
1946
0
5
4
5
余数
30241(5)=5450(7)
小结作业
1.利用除k取余法,可以把任何一个十进制数化为k进制数,并且操作简单、实用.
2.通过k进制数与十进制数的转化,我们也可以将一个k进制数转化为另一个不同基数的k进制数.
作业:
P45练习:3.
P48习题1.3A组:3,4.
1.3 算法案例
第2课时 秦九韶算法与进位制
2019.11
课程标准 学习要求 数学素养
通过阅读中国古代数学中的算法案例,体会中国古代数学对世界数学发展的贡献 1.了解算法的含义,体会算法的思想
2.在分析案例的基础上了解算法的基本特征
3.理解秦九韶算法的计算过程,并了解它提高计算效率的实质.
4理解进位制的概念,能进行不同进位制间的转化.
数学抽象
数学运算
逻辑推理
课堂探究
思考1 按我们平时的求解方法,把x的值代入多项式,计算各项
的值,然后相加共做了多少乘法、加法次运算?
阅读课本P37~38页
探究一:怎样求多项式 时的值呢?
答案 4+3+2+1=10次乘法运算,5次加法运算
思考2 如果我们先计算 ,然后再依次计算
的值,然后相加共做了多少乘法、加法次运算?
答案 4次乘法运算,5次加法运算
课堂探究
比较上述两种方法,第二种乘法运算次数减少了,因而能提高运算效率,对计算机来说,做一次乘法运算所用时间比作一次加法运算要长得多,所以采用第二种做法,计算机能更快得到结果。这就是我国南宋时期的数学家秦九韶在《数书九章》中提出的算法----秦九韶算法
探究一:怎样求多项式 时的值呢?
课堂探究
探究二:秦九韶算法及其应用
思考3 衡量一个算法是否优秀的重要参数是速度.把多项式f(x)=x5+x4+x3+x2+x+1变形为f(x)=((((x+1)x+1)x+1)x+1)x+1,然后求当x=5时的值,为什么比常规逐项计算省时?
答案 从里往外计算,充分利用已有成果,可减少重复计算.
探究一:怎样求多项式 时的值呢?
解:根据秦九韶算法,把多项式改写成如下形式:
按照从内到外的顺序,依次计算一次多项式当x=5时的值:
所以当x=5时,多项式的值为3906
思考4:利用后一种算法求多项式f(x)=anxn+an-1xn-1
+…+a1x+a0的值,这个多项式应写成哪种形式?
f(x)=anxn+an-1xn-1+…+a1x+a0
=(anxn-1+an-1xn-2+…+a2x+a1)x+a0
=((anxn-2+an-1xn-3+…+a2)x+a1)x+a0 =…
=(…((anx+an-1)x+an-2)x+…+a1)x+a0.
思考5:对于f(x)=(…((anx+an-1)x+ an-2)x+…+a1)x+a0,由内向外逐层计算一次多项式的值,其算法步骤如何?
第一步,计算v1=anx+an-1.
第二步,计算v2=v1x+an-2.
第三步,计算v3=v2x+an-3.
…
第n步,计算vn=vn-1x+a0.
思考6:上述求多项式f(x)=anxn+an-1xn-1+…+a1x+a0的值的方法称为秦九韶算法,利用该算法求f(x0)的值,一共需要多少次乘法运算,多少次加法运算?
思考7:在秦九韶算法中,记v0=an,那么第k步的算式是什么?
vk=vk-1x+an-k (k=1,2,…,n)
n次乘法,n次加法
秦九韶算法原理、程序框图及其相应程序
把一个n次多项式f(x)=anxn+an-1xn-1+…+a1x+a0改写成如下形式:(…((anx+an-1)x+an-2)x+…+a1)x+a0,求多项式的值时,首先计算
一次多项式的值,即v1= , 然后由内向外逐层计算一次多项式的值,即v2= ,
v3= ,…
vn= ,
这样,求n次多项式f(x)的值就转化为求 的值.
anx+an -1
最内层括号内
v1x+an-2
v2x+an-3
vn-1x+a0
n个一次多项式
秦九韶算法的原理
秦九韶算法的程序设计
用秦九韶算法求多项式的值,可以用什么逻辑结构来构造算法?其算法步骤如何设计?
第一步,输入多项式的次数n,最高次项的系数an和x的值.
第二步,令v=an,i=n-1.
第三步,输入i次项的系数ai.
第四步,v=vx+ai,i=i-1.
第五步,判断i≥0是否成立.若是,则返回第 二步;否则,输出多项式的值v.
该算法的程序框图
开始
输入n,an,x的值
v=an
v=vx+ai
输入ai
i=n-1
i=i-1
i≥0?
是
输出v
否
结束
该程序框图对应的程序如何表述?
开始
输入n,an,x的值
v=an
v=vx+ai
输入ai
i≥0?
i=n-1
i=i-1
结束
是
输出v
否
INPUT “n=”;n
INPUT “an=”;a
INPUT “x=”;x
v=an
i=n-1
WHILE i>=0
INPUT “ai=”;b
v=v*x+b
i=i-1
WEND
PRINT y
END
例1:已知一个5次多项式 ,,用秦九韶算法求这个多项式当x=5时的值呢。
解:根据秦九韶算法,把多项式改写成如下形式:
按照从内到外的顺序,依次计算一次多项式当x=5时的值:
所以当x=5时,多项式的值为14130.2
例2 阅读下列程序,说明它解决的实际问题是什么?
INPUT “x=”;a
n=0
y=0
WHLE n<5
y=y+(n+1)*a?n
n=n+1
WEND
PRINT y
END
求多项式 在x=a时的值.
归纳小结
评价一个算法好坏的一个重要标志是运算的次数,如果一个算法从理论上需要超出计算机允许范围内的运算次数,那么这样的算法就只能是一个理论算法.在多项式求值的各种算法中,秦九韶算法是一个优秀算法.
作业:
P45练习:2.
P48习题1.3A组:2.
阅读课本P40~45页完成下列问题:
1.进位制的概念
位制是人们为了_____和_____方便而约定的记数系统,“满几进一”就是_____制,_____制的基数(基数都是大于1的整数)就是___.
常见的进位制有二进制,七进制(一周7天)、十进制(我们最熟悉的进位制),十二进制(一年12个月)及六十进制(一小时60分钟).
计数
几
几进
运算
几进制
2. k进制数的表示方法
一般地,若k是一个大于1的整数,那么以k为基数的k进制数可以表示为一串数字连写在一起的形式:anan-1an-2…a1a0(k)(an,an-1,…,a1,a0∈N,0<an<k,0≤an-1,…,a1,a0<k).
3. k进制数与10进制数的转化
①由k进制anan-1an-2…a1a0(k)转化为10进制数
anan-1an-2…a1a0(k)
=an×kn+an-1×kn-1+an-2×kn-2+…+a1×k+a0×k0;
②由10进制数转化为k进制数——除k取余法.
课堂探究:除k取余法
思考1:二进制数101101(2)化为十进制数是什么数?十进制数89化为二进制数是什么数?
101101(2)=25+23+22+1=45.
89=2×(2×(2×(2×(2×2+1)+1)+0)+0)+1
=1×26+0×25+1×24+1×23+0×22+0×21+1×20=1011001(2).
思考2:上述化十进制数为二进制数的算法叫做除2取余法,转化过程有些复杂,观察下面的算式你有什么发现吗?
2
1
2
2
2
5
0
2
11
2
22
2
44
2
89
1
0
0
1
1
0
1
余数
89=2×(2×(2×(2×(2×(2×(2×0+1)+0)+1)+1)+0)+0)+1
=2×(2×(2×(2×(22+0×21+1)+1)+0)+0)+1
=2×(2×(2×(23+0×22+1×21+1)+0)+0)+1
=…
=1×26+0×25+1×24+1×23+0×22+0×21+1×20
=101101(2)
思考3:上述方法也可以推广为把十进制数化为k进制数的算法,称为除k取余法,那么十进制数191化为五进制数是什么数?
0
5
1
5
7
5
38
5
191
1
3
2
1
余数
191=1231(5)
若十进制数 a除以2所得的商是q0,余数是r0, 即a=2×q0+ r0;
q0除以2所得的商是q1,余数是r1,即q0=2×q1+ r1;
……
qn-1除以2所得的商是0,余数是rn, 即qn-1= 2×0+rn,
那么十进制数a化为二进制数是什么数?
a=rnrn-1…r1r0(2)
思考4:
十进制化k进制的算法
思考1:根据上面的分析,将十进制数a化为二进制数的算法步骤如何设计?
第四步,若q≠0,则a=q,返回第二步;
否则,输出全部余数r排列得到的二进制数.
第一步,输入十进制数a的值.
第二步,求出a除以2所得的商q,余数r.
第三步,把所得的余数依次从右到左排列.
利用除k取余法,将十进制数a化为k进制数b的算法步骤如何设计?
第四步,若q≠0,则a=q,返回第二步;否则,输出全部余数r排列得到的k进制数.
第一步,输入十进制数a和基数k的值.
第二步,求出a除以k所得的商q,余数r.
第三步,把所得的余数依次从右到左排成一列.
将除k取余法的算法步骤用程序框图如何表示?
开始
输入a,k
求a除以k的商q
求a除以k的余数r
把所得的余数依次从右到左排成一列
a=q
q=0?
结束
输出全部余数r排列得到的k进制数
是
否
该程序框图对应的程序如何表述?
开始
输入a,k
求a除以k的商q
求a除以k的余数r
把所得的余数依次从右到左排列
a=q
q=0?
结束
输出全部余数r排
列得到的k进制数
是
否
INPUT “a,k=” a,k
b=0
i=0
DO
q=a\k
r=a MOD k
b=b+r*10∧i
i=i+1
a=q
LOOP UNTIL q=0
PRINT b
END
例1 将十进制数458分别转化为四进制数和六进制数.
0
4
1
4
7
4
28
4
114
4
458
2
2
0
3
1
余数
0
6
2
6
12
6
76
6
458
2
4
0
2
余数
458=13022(4)=2042(6)
例2 将五进制数3241(5)转化为七进制数.
30241(5)=3×54+2×52+4×5+1=1946.
0
7
5
7
39
7
278
7
1946
0
5
4
5
余数
30241(5)=5450(7)
小结作业
1.利用除k取余法,可以把任何一个十进制数化为k进制数,并且操作简单、实用.
2.通过k进制数与十进制数的转化,我们也可以将一个k进制数转化为另一个不同基数的k进制数.
作业:
P45练习:3.
P48习题1.3A组:3,4.
