2019-2020学年江苏省南通市启东市高三(上)期中数学试卷试题及答案(word版含答案解析)
文档属性
| 名称 | 2019-2020学年江苏省南通市启东市高三(上)期中数学试卷试题及答案(word版含答案解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 229.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-11 00:00:00 | ||
图片预览





文档简介
2019-2020学年江苏省南通市启东市高三(上)期中数学试卷
一、填空题:本大题共14小题,每小题5分,共70分.不需写出解答过程,请把答案直接填写在答题卡相应位置上.
1.已知集合A={x|﹣2<x<1},B={﹣2,﹣1,0,1,2},则A∩B= .
2.函数的最小正周期为 .
3.“x>3”是“x2﹣3x+2>0”的 条件.(从“充要”,“充分不必要”,“必要不充分”,“既不充分又不必要”中选择一个正确的填写)
4.在△ABC中,角A,B,C的对边分别为a,b,c,若acosB=2bsinA,则cosB= .
5.记Sn是等比数列{an}的前n项和,a1+a2=2,a4+a5=4,则 .
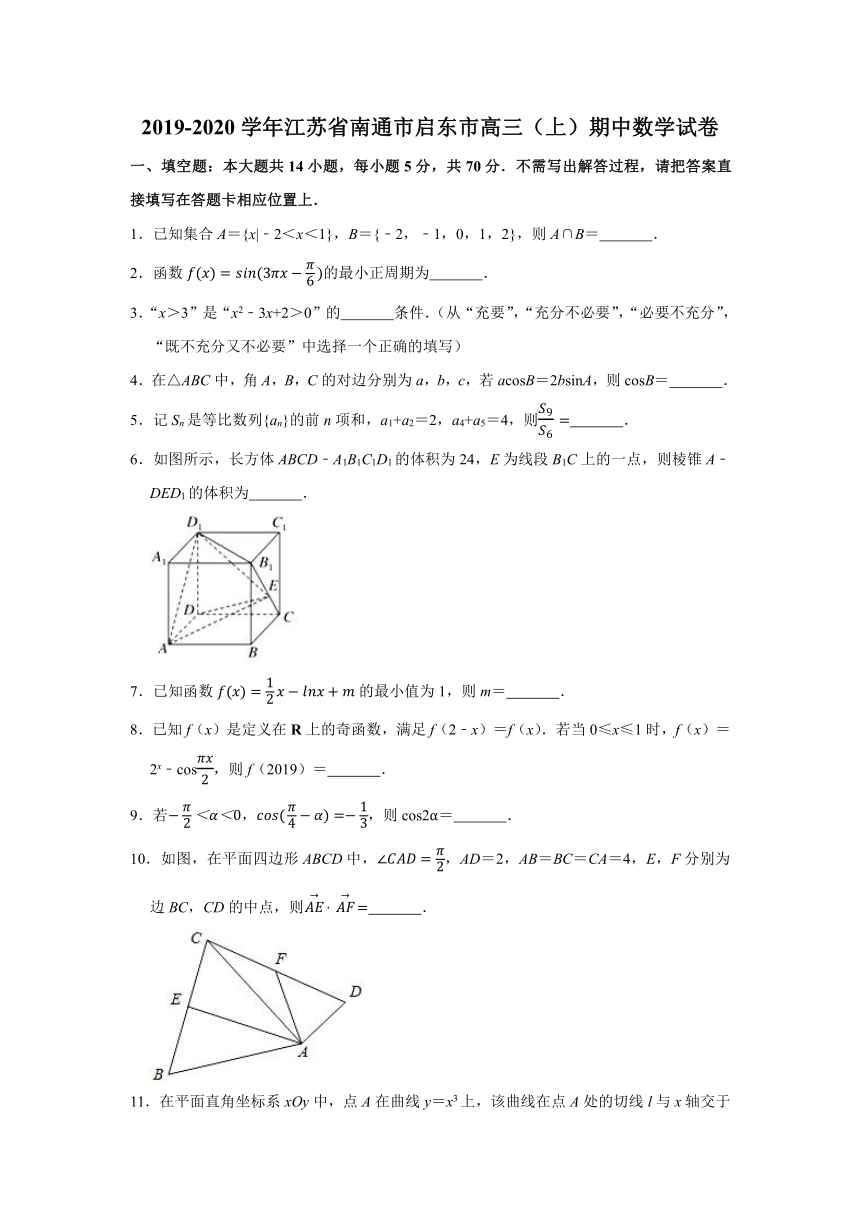
6.如图所示,长方体ABCD﹣A1B1C1D1的体积为24,E为线段B1C上的一点,则棱锥A﹣DED1的体积为 .
7.已知函数的最小值为1,则m= .
8.已知f(x)是定义在R上的奇函数,满足f(2﹣x)=f(x).若当0≤x≤1时,f(x)=2x﹣cos,则f(2019)= .
9.若,,则cos2α= .
10.如图,在平面四边形ABCD中,,AD=2,AB=BC=CA=4,E,F分别为边BC,CD的中点,则 .
11.在平面直角坐标系xOy中,点A在曲线y=x3上,该曲线在点A处的切线l与x轴交于点B.若AC⊥x轴,垂足为C,且BC长为1,则切线l的斜率为 .
12.已知函数则不等式f(x+2)>f(x)的解集是 .
13.若函数f(x)=ax﹣x3(a>0,a≠1)有两个不同的零点,则a的取值范围是 .
14.如图,在△ABC中,D,E是BC上的两个三等分点,,则cosB的最小值为 .
二、解答题:本大题共10小题,共90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
15.如图,在四棱锥P﹣ABCD中,底面ABCD是平行四边形,E为棱PD的中点,平面PAB⊥底面ABCD,∠PAB=90°.求证:
(1)PB∥平面AEC;
(2)平面PAC⊥平面ABCD.
16.已知,(sinx,1),.
(1)若||,求cos2x的值;
(2)求函数f(x)?的单调区间和值域.
17.已知函数f(x)=ax+bx(a>0,a≠1,b>0,b≠1)是偶函数.
(1)求ab的值;
(2)若f(lgx)<f(1),求x的取值范围.
18.如图,某登山队在山脚A处测得山顶B的仰角为45°,沿倾斜角为α(其中tanα)的斜坡前进km后到达D处,休息后继续行驶km到达山顶B.
(1)求山的高度BE;
(2)现山顶处有一塔CBkm.从A到D的登山途中,队员在点P处测得塔的视角为θ(∠CPB=θ).若点P处高度PF为xkm,则x为何值时,视角θ最大?
19.已知函数f(x)(a∈R).
(1)当a=0时,求f(x)的极值;
(2)若f(x)在区间(0,2)内有两个极值点,求实数a的取值范围.
20.数列{an}的各项均为正数,其前n项和为Sn.已知对任意的n∈N*,存在实数p,q满足.
(1)若an=2n,求p,q的值;
(2)若a1,a2,a3成等差数列,求证:数列{an}是等差数列.
21.在空间直角坐标系O﹣xyz中,O(0,0,0),A(1,0,0),B(1,2,0),C(0,1,2),点P满足.
(1)求点P的坐标(用λ表示);
(2)若OP⊥BC,求λ的值.
确定函数f(x)=cos2x+4cosx,x∈(0,2π)的单调区间.
23.在直四棱柱ABCD﹣A1B1C1D1中,AB⊥AC,AB=1,AC=AA1=2,.
(1)求二面角D1﹣AC﹣B1的余弦值;
(2)试问线段A1B1上是否存在点E,使得直线DE∥平面ACB1?若存在,求线段A1E的长;若不存在,说明理由.
24.已知x>1,,,n∈N*.
(1)比较S2(x)与T2(x)的大小;
(2)比较Sn(x)与Tn(x)(n∈N*)大小,并加以证明.
2019-2020学年江苏省南通市启东市高三(上)期中数学试卷
参考答案与试题解析
一、填空题:本大题共14小题,每小题5分,共70分.不需写出解答过程,请把答案直接填写在答题卡相应位置上.
1.已知集合A={x|﹣2<x<1},B={﹣2,﹣1,0,1,2},则A∩B= {﹣1,0} .
【解答】解:∵A={x|﹣2<x<1},B={﹣2,﹣1,0,1,2},
∴A∩B={﹣1,0}.
故答案为:{﹣1,0}.
2.函数的最小正周期为 .
【解答】解:函数的最小正周期为 ,
故答案:.
3.“x>3”是“x2﹣3x+2>0”的 充分不必要 条件.(从“充要”,“充分不必要”,“必要不充分”,“既不充分又不必要”中选择一个正确的填写)
【解答】解:由x2﹣3x+2>0,解得x<1或x>2.
则由x>3?x2﹣3x+2>0;反之不成立.
∴“x>3”是“x2﹣3x+2>0”的充分不必要条件.
故答案为:充分不必要.
4.在△ABC中,角A,B,C的对边分别为a,b,c,若acosB=2bsinA,则cosB= .
【解答】解:∵acosB=2bsinA,
∴由正弦定理,则有sinAcosB=2sinBsinA,
∵△ABC中∠A不可能为π,∴sinA≠0,∴得到cosB=2sinB……①,
又sin2B+cos2B=1……②
解①②得cosB=±,
因为∠B为三角形内角,所以sinB>0,
所以cosB=2sinB>0,
∴cosB.
5.记Sn是等比数列{an}的前n项和,a1+a2=2,a4+a5=4,则 .
【解答】解:设等比数列{an}的公比为q,∵a1+a2=2,a4+a5=4,
∴a1(1+q)=2,a1q3(1+q)=4,
∴q3=2,
则.
故答案为:.
6.如图所示,长方体ABCD﹣A1B1C1D1的体积为24,E为线段B1C上的一点,则棱锥A﹣DED1的体积为 4 .
【解答】解:设长方体ABCD﹣A1B1C1D1的三条棱长分别为AB=a,AD=b,AA1=c,
则长方体的体积为V长方体=abc=24,
所以三棱锥A﹣DED1的体积为
V三棱锥?hAD×DD1×ABbc?a24=4.
故答案为:4.
7.已知函数的最小值为1,则m= ln2 .
【解答】解:f(x)的定义域是(0,+∞),
f′(x),
令f′(x)>0,解得:x>2,
令f′(x)<0,解得:0<x<2,
故f(x)在(0,2)递减,在(2,+∞)递增,
故f(x)min=f(2)=1﹣ln2+m=1,解得:m=ln2,
故答案为:ln2.
8.已知f(x)是定义在R上的奇函数,满足f(2﹣x)=f(x).若当0≤x≤1时,f(x)=2x﹣cos,则f(2019)= ﹣2 .
【解答】解:根据题意,f(x)是定义在R上的奇函数,则f(x)=﹣f(﹣x),
又由f(x)满足f(2﹣x)=f(x),则有f(2﹣x)=﹣f(﹣x),即f(x+2)=﹣f(x),
变形可得:f(x+4)=﹣f(x+2)=f(x),即函数f(x)是周期为4的周期函数,
则f(2019)=f(2020﹣1)=f(﹣1)=﹣f(1),
若当0≤x≤1时,f(x)=2x﹣cos,则f(1)=2﹣cos2,
则有f(2019)=﹣2;
故答案为:﹣2.
9.若,,则cos2α= .
【解答】解:若,,则sin(α)
则cos2α=sin(2α)=2sin(α)cos(α),
故答案为:.
10.如图,在平面四边形ABCD中,,AD=2,AB=BC=CA=4,E,F分别为边BC,CD的中点,则 .
【解答】解:如图所示,
∵E为BC中点,
∴,
同理,
∴??,
其中∠BAD=150°,∠BAC=60°,∠CAD=90°,
∴,,
,,
∴.
故答案为:.
11.在平面直角坐标系xOy中,点A在曲线y=x3上,该曲线在点A处的切线l与x轴交于点B.若AC⊥x轴,垂足为C,且BC长为1,则切线l的斜率为 27 .
【解答】解:由题意,设点A坐标为(x0,y0).
∵y′=3x2,∴y′|x=x0=3.
故曲线在点A处的切线l的斜率k=3.
∵y0,
∴切线l的直线方程为y3?(x﹣x0),
整理,得:y=3?x﹣2.
由题意知,B点坐标为(,0),C点坐标为(x0,0).
∴x01,解得x0=3.
∴切线l的斜率k=327.
故答案为:27.
12.已知函数则不等式f(x+2)>f(x)的解集是 (﹣∞,0)∪(3,+∞) .
【解答】解:若x>1,由f(x+2)>f(x)得(x+2)2﹣8(x+2)+8>x2﹣8x+8,
即4x>12,x>3,此时x>3成立,
若x+2≤1,即x≤﹣1时,由f(x+2)>f(x)得5(x+2)﹣4>5x﹣4,
得10>0,成立,此时x≤﹣1,
若﹣1<x≤1,则由f(x+2)>f(x)得(x+2)2﹣8(x+2)+8>5x﹣4,
即x2﹣9x>0,得x>9或x<0,
此时﹣1<x<0,
综上x<0或x>3,
即不等式的解集为(﹣∞,0)∪(3,+∞),
故答案为:(﹣∞,0)∪(3,+∞)
13.若函数f(x)=ax﹣x3(a>0,a≠1)有两个不同的零点,则a的取值范围是 .
【解答】解:∵f(x)=ax﹣x3(a>0,a≠1)有两个不同的零点,
∴等价于ax=x3恰有两个不同解.
当0<a<1,y=ax与y=﹣x3的图象只有一个交点,
不符合题意.
当a>1时,y=ax与y=﹣x3的图象在x∈(﹣∞,0)
上没有交点,
∴只考虑x>0,
于是两边取对数,得xlna=3lnx,即lna,
令g(x),则g′(x),
当x∈(0,e)时,g(x)单调递增,
当x<1时,g(x)<0,
x∈(e,+∞)时,g(x)单调递减且g(x)>0.
∴要有两个交点,0<lna<g(e),即1<a.
故答案为.
14.如图,在△ABC中,D,E是BC上的两个三等分点,,则cosB的最小值为 .
【解答】解:∵,
∴,
∴,
∴,
∴,
∴,
∴,
∴,
∴在△ABC中,2c2=4b2+bccos∠BAC,
∴2c2=4b2+bc,
∴b2,
∴cosB(当且仅当时,取“=”),
故cosB的最小值是:.
故答案为:.
二、解答题:本大题共10小题,共90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
15.如图,在四棱锥P﹣ABCD中,底面ABCD是平行四边形,E为棱PD的中点,平面PAB⊥底面ABCD,∠PAB=90°.求证:
(1)PB∥平面AEC;
(2)平面PAC⊥平面ABCD.
【解答】证明:(1)连BD,交AC于点O,连OE.因为底面ABCD是平行四边形,所以O为BD的中点.
因为E为棱PD的中点,所以OE∥PB,
又因为OE?平面AEC,PB?平面AEC,
所以PB∥平面AEC.
(2)因为平面PAB⊥底面ABCD,∠PAB=90°,
平面PAB∩平面ABCD=AB,PA?平面PAB,
所以PA⊥平面ABCD,
因为PA?平面PAC,
所以平面PAC⊥平面ABCD.
16.已知,(sinx,1),.
(1)若||,求cos2x的值;
(2)求函数f(x)?的单调区间和值域.
【解答】解:(1)因为,所以,
即,
所以.
因为,
所以,
因为,
所以,
所以.
所以.
(2)因为,
因为,所以x∈[,0],
当x∈[,]时,即时,f(x)单调递减;
当,
即时,f(x)单调递增;
故函数f(x)的单调增区间,单调减区间.
由于∈[﹣1,0],所以函数f(x)的值域为[﹣1,0].
17.已知函数f(x)=ax+bx(a>0,a≠1,b>0,b≠1)是偶函数.
(1)求ab的值;
(2)若f(lgx)<f(1),求x的取值范围.
【解答】解:(1)因为f(x)是偶函数,所以对任意实数x,有f(x)﹣f(﹣x)=0
即,
所以(axbx﹣1)(ax+bx)=0对任意实数x成立,
因为ax>0,bx>0,
所以axbx﹣1=0,即(ab)x=1对任意实数x成立,
所以ab=1.
(2)由(1)知,此时,
因为a>0,a≠1,b>0,b≠1,故不妨设a>1,
任取0≤x1<x2,
则,
因为0≤x1<x2,a>1,所以,
所以,,
所以f(x1)﹣f(x2)<0,
即f(x1)<f(x2),
所以f(x)在[0,+∞)上单调递增,
因为f(lg x)<f(1),
所以f(|lgx|)<f(1),
所以|lgx|<1,解得.
即不等式的解集为(,10).
18.如图,某登山队在山脚A处测得山顶B的仰角为45°,沿倾斜角为α(其中tanα)的斜坡前进km后到达D处,休息后继续行驶km到达山顶B.
(1)求山的高度BE;
(2)现山顶处有一塔CBkm.从A到D的登山途中,队员在点P处测得塔的视角为θ(∠CPB=θ).若点P处高度PF为xkm,则x为何值时,视角θ最大?
【解答】解:(1)方法一:因为,α是锐角,所以,,
所以;
在△ABD中,过D作DM⊥AB,垂足为M,
如图1所示;
因为,
所以;
在△ABE中,BE=ABcos45°=3,
所以山的高度为3 km.
方法二:过D作DG⊥AE于点G,过D作DH⊥BE于点H,如图2所示;
在△ADG中,∠DAG=α,,所以,,
所以,;
设BE=h,在直角△BDH中,BH=h﹣1,DH=h﹣2,
由于BD2=BH2+DH2,所以,
因为h>0,所以h=3;
所以山的高度为3 km.
(2)过P作PN⊥BE于N,如图3所示;
因为PF=x,所以AF=2x,
因为P在AD上,DG=1,所以x∈[0,1],
所以tan∠BPN,tan∠CPN,
所以tanθ=tan(∠CPN﹣∠BPN),x∈[0,1];
令t=3﹣2x∈[1,3],所以,
则tanθ,
当且仅当,即时,即时tanθ取得最大值.
所以,当km时,视角θ最大.
19.已知函数f(x)(a∈R).
(1)当a=0时,求f(x)的极值;
(2)若f(x)在区间(0,2)内有两个极值点,求实数a的取值范围.
【解答】解:(1)因为a=0,所以f(x),
所以f′(x),令f'(x)=0得x=2.列表如下.
x (0,2) 2 (2,+∞)
f′(x) ﹣ 0 +
f(x) ↘ 极小值f(2) ↗
因此,当x=2时,f(x)有极小值f(2)=ln2+1,无极大值;
(2)因为f′(x),
由0<x<2,得,
记g(x)=x﹣aex,x∈(0,2),
因为f(x)在区间(0,2)内有两个极值点,
所以g(x)在区间(0,2)内有两个零点,
所以g'(x)=1﹣aex且a>0,
令g'(x)=0,则x=﹣lna,
①当﹣lna≤0,即a≥1时,g'(x)<0,
所以g(x)在(0,2)上单调递减,至多与x轴有一个交点,不满足题意;
②当﹣ln a≥2,即0<a时,g'(x)>0,
所以g(x)在(0,2)上单调递增,至多与x轴有一个交点,不满足题意;
③当0<﹣ln a<2,即时,g(x)在(0,﹣ln a)上单调递增,
在(﹣ln a,2)上单调递减;
由g(0)=﹣a<0,要使g(x)在区间(0,2)内有两个零点,
必须满足解得,
综上所述,实数a的取值范围是.
20.数列{an}的各项均为正数,其前n项和为Sn.已知对任意的n∈N*,存在实数p,q满足.
(1)若an=2n,求p,q的值;
(2)若a1,a2,a3成等差数列,求证:数列{an}是等差数列.
【解答】(1)解:∵an=2n,∴数列{an}是首项为2,公差为2的等差数列,
∴,
代入得,n2+n=4pn2+qn,
∵上式对n∈N*恒成立,∴,
故;
(2)证明:∵a1,a2,a3成等差数列,设公差为d≥0,
则,即 ,
②﹣①×2,③﹣①×3得,,
⑤﹣④×3得,,∴p=0或a1=d,
1°当p=0时,Sn=qn,∴an=q,
∴an+1﹣an=0,
∴{an}是以q为首项,0为公差的等差数列.
2°当a1=d时,则d>0,代入④,①得,,,
∴,,
两式相减得,,
得,
∴an+1+an=d或an+1﹣an=d,
∵a1=d>0,a1,a2,a3成等差数列,
∴a2=2d,a3=3d,下面证明an+1﹣an=d对n∈N*恒成立,
假设an+1+an=d成立的最小n值为k,即ak+1+ak=d,显然k≥3,
又ak﹣ak﹣1=d,
两式相减得,ak+1+ak﹣1=0,这与an>0,n∈N*矛盾,
因此,an+1﹣an=d,n∈N*,
∴{an}是以d为首项d为公差的等差数列.
综合1°2°,数列{an}是等差数列.
21.在空间直角坐标系O﹣xyz中,O(0,0,0),A(1,0,0),B(1,2,0),C(0,1,2),点P满足.
(1)求点P的坐标(用λ表示);
(2)若OP⊥BC,求λ的值.
【解答】解:(1)因为A(1,0,0),C(0,1,2),
所以,
因为,
所以,
所以点P的坐标为(1﹣λ,λ,2λ).
(2)因为,OP⊥BC,
所以,即﹣1×(1﹣λ)﹣1×λ+2×2λ=0,
解得.
22.确定函数f(x)=cos2x+4cosx,x∈(0,2π)的单调区间.
【解答】解:函数的导数f'(x)=﹣2sin2x﹣4sinx=﹣4sinx(cosx+1),
令f'(x)>0,sinx<0,
又x∈(0,2π),所以π<x<2π;
令f'(x)<0,sinx>0,
又x∈(0,2π),所以0<x<π.
故f(x)的单调增区间为(π,2π),单调减区间为(0,π).
23.在直四棱柱ABCD﹣A1B1C1D1中,AB⊥AC,AB=1,AC=AA1=2,.
(1)求二面角D1﹣AC﹣B1的余弦值;
(2)试问线段A1B1上是否存在点E,使得直线DE∥平面ACB1?若存在,求线段A1E的长;若不存在,说明理由.
【解答】解:(1)在直四棱柱ABCD﹣A1B1C1D1中,AA1⊥平面ABCD,
因为AB?平面ABCD,AC?平面ABCD,所以AA1⊥AB,AA1⊥AC,
因为AB⊥AC,所以以A为坐标原点,AC,AB,AA1分别为x,y,z轴建立空间直角坐标系,
如图所示.
依题意可得A(0,0,0),B(0,1,0),C(2,0,0),D(1,﹣2,0),
A1(0,0,2),B1(0,1,2),C1(2,0,2),D1(1,﹣2,2).
设为平面ACB1的法向量,则
因为,所以
不妨设z=1,可得.
设为平面ACD1的法向量,则
因为,所以
不妨设z=1,可得.
所以.
由图知,二面角D1﹣AC﹣B1为锐角,
所以二面角D1﹣AC﹣B1的余弦值为.
(2)假设线段A1B1上是否存在点E,使得直线DE∥平面ACB1,则,
设A1E=a,0≤a≤1,则E(0,a,2),.
所以,
所以a=﹣1,不合题意,故舍去.
所以,线段A1B1上不存在点E,使直线DE∥平面ACB1.
24.已知x>1,,,n∈N*.
(1)比较S2(x)与T2(x)的大小;
(2)比较Sn(x)与Tn(x)(n∈N*)大小,并加以证明.
【解答】解:(1)S2(x)﹣T2(x)
,
因为x>1,所以,
所以S2(x)﹣T2(x)<0,所以S2(x)<T2(x);
(2)本题结论为Sn(x)≤Tn(x),n∈N*,证明如下:
要证Sn(x)≤Tn(x),n∈N*,只要证,n∈N*,
只要证,n∈N*,
因为x>1,所以只要证,n∈N*,(*)
下面用数学归纳法证明:
①当n=1时,(*)式成立.
②假设当n=k时,(*)式成立,即有,
则当n=k+1时,(*)式左边,
而此时(*)式右边,
所以只要证,
只要证kxk+1﹣(k+1)xk+1≥0,(**)
令f(x)=kxk+1﹣(k+1)xk+1,x>1,k∈N*,
因为f'(x)=k(k+1)xk﹣k(k+1)xk﹣1=k(k+1)xk﹣1(x﹣1)>0,
所以f(x)在(1,+∞)上单调递增,所以f(x)>f(1)=0,
故(**)式成立.这就是说,当n=k+1时,(*)式也成立,
综合①②可知(*)式成立,
所以Sn(x)≤Tn(x),n∈N*成立,得证.
一、填空题:本大题共14小题,每小题5分,共70分.不需写出解答过程,请把答案直接填写在答题卡相应位置上.
1.已知集合A={x|﹣2<x<1},B={﹣2,﹣1,0,1,2},则A∩B= .
2.函数的最小正周期为 .
3.“x>3”是“x2﹣3x+2>0”的 条件.(从“充要”,“充分不必要”,“必要不充分”,“既不充分又不必要”中选择一个正确的填写)
4.在△ABC中,角A,B,C的对边分别为a,b,c,若acosB=2bsinA,则cosB= .
5.记Sn是等比数列{an}的前n项和,a1+a2=2,a4+a5=4,则 .
6.如图所示,长方体ABCD﹣A1B1C1D1的体积为24,E为线段B1C上的一点,则棱锥A﹣DED1的体积为 .
7.已知函数的最小值为1,则m= .
8.已知f(x)是定义在R上的奇函数,满足f(2﹣x)=f(x).若当0≤x≤1时,f(x)=2x﹣cos,则f(2019)= .
9.若,,则cos2α= .
10.如图,在平面四边形ABCD中,,AD=2,AB=BC=CA=4,E,F分别为边BC,CD的中点,则 .
11.在平面直角坐标系xOy中,点A在曲线y=x3上,该曲线在点A处的切线l与x轴交于点B.若AC⊥x轴,垂足为C,且BC长为1,则切线l的斜率为 .
12.已知函数则不等式f(x+2)>f(x)的解集是 .
13.若函数f(x)=ax﹣x3(a>0,a≠1)有两个不同的零点,则a的取值范围是 .
14.如图,在△ABC中,D,E是BC上的两个三等分点,,则cosB的最小值为 .
二、解答题:本大题共10小题,共90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
15.如图,在四棱锥P﹣ABCD中,底面ABCD是平行四边形,E为棱PD的中点,平面PAB⊥底面ABCD,∠PAB=90°.求证:
(1)PB∥平面AEC;
(2)平面PAC⊥平面ABCD.
16.已知,(sinx,1),.
(1)若||,求cos2x的值;
(2)求函数f(x)?的单调区间和值域.
17.已知函数f(x)=ax+bx(a>0,a≠1,b>0,b≠1)是偶函数.
(1)求ab的值;
(2)若f(lgx)<f(1),求x的取值范围.
18.如图,某登山队在山脚A处测得山顶B的仰角为45°,沿倾斜角为α(其中tanα)的斜坡前进km后到达D处,休息后继续行驶km到达山顶B.
(1)求山的高度BE;
(2)现山顶处有一塔CBkm.从A到D的登山途中,队员在点P处测得塔的视角为θ(∠CPB=θ).若点P处高度PF为xkm,则x为何值时,视角θ最大?
19.已知函数f(x)(a∈R).
(1)当a=0时,求f(x)的极值;
(2)若f(x)在区间(0,2)内有两个极值点,求实数a的取值范围.
20.数列{an}的各项均为正数,其前n项和为Sn.已知对任意的n∈N*,存在实数p,q满足.
(1)若an=2n,求p,q的值;
(2)若a1,a2,a3成等差数列,求证:数列{an}是等差数列.
21.在空间直角坐标系O﹣xyz中,O(0,0,0),A(1,0,0),B(1,2,0),C(0,1,2),点P满足.
(1)求点P的坐标(用λ表示);
(2)若OP⊥BC,求λ的值.
确定函数f(x)=cos2x+4cosx,x∈(0,2π)的单调区间.
23.在直四棱柱ABCD﹣A1B1C1D1中,AB⊥AC,AB=1,AC=AA1=2,.
(1)求二面角D1﹣AC﹣B1的余弦值;
(2)试问线段A1B1上是否存在点E,使得直线DE∥平面ACB1?若存在,求线段A1E的长;若不存在,说明理由.
24.已知x>1,,,n∈N*.
(1)比较S2(x)与T2(x)的大小;
(2)比较Sn(x)与Tn(x)(n∈N*)大小,并加以证明.
2019-2020学年江苏省南通市启东市高三(上)期中数学试卷
参考答案与试题解析
一、填空题:本大题共14小题,每小题5分,共70分.不需写出解答过程,请把答案直接填写在答题卡相应位置上.
1.已知集合A={x|﹣2<x<1},B={﹣2,﹣1,0,1,2},则A∩B= {﹣1,0} .
【解答】解:∵A={x|﹣2<x<1},B={﹣2,﹣1,0,1,2},
∴A∩B={﹣1,0}.
故答案为:{﹣1,0}.
2.函数的最小正周期为 .
【解答】解:函数的最小正周期为 ,
故答案:.
3.“x>3”是“x2﹣3x+2>0”的 充分不必要 条件.(从“充要”,“充分不必要”,“必要不充分”,“既不充分又不必要”中选择一个正确的填写)
【解答】解:由x2﹣3x+2>0,解得x<1或x>2.
则由x>3?x2﹣3x+2>0;反之不成立.
∴“x>3”是“x2﹣3x+2>0”的充分不必要条件.
故答案为:充分不必要.
4.在△ABC中,角A,B,C的对边分别为a,b,c,若acosB=2bsinA,则cosB= .
【解答】解:∵acosB=2bsinA,
∴由正弦定理,则有sinAcosB=2sinBsinA,
∵△ABC中∠A不可能为π,∴sinA≠0,∴得到cosB=2sinB……①,
又sin2B+cos2B=1……②
解①②得cosB=±,
因为∠B为三角形内角,所以sinB>0,
所以cosB=2sinB>0,
∴cosB.
5.记Sn是等比数列{an}的前n项和,a1+a2=2,a4+a5=4,则 .
【解答】解:设等比数列{an}的公比为q,∵a1+a2=2,a4+a5=4,
∴a1(1+q)=2,a1q3(1+q)=4,
∴q3=2,
则.
故答案为:.
6.如图所示,长方体ABCD﹣A1B1C1D1的体积为24,E为线段B1C上的一点,则棱锥A﹣DED1的体积为 4 .
【解答】解:设长方体ABCD﹣A1B1C1D1的三条棱长分别为AB=a,AD=b,AA1=c,
则长方体的体积为V长方体=abc=24,
所以三棱锥A﹣DED1的体积为
V三棱锥?hAD×DD1×ABbc?a24=4.
故答案为:4.
7.已知函数的最小值为1,则m= ln2 .
【解答】解:f(x)的定义域是(0,+∞),
f′(x),
令f′(x)>0,解得:x>2,
令f′(x)<0,解得:0<x<2,
故f(x)在(0,2)递减,在(2,+∞)递增,
故f(x)min=f(2)=1﹣ln2+m=1,解得:m=ln2,
故答案为:ln2.
8.已知f(x)是定义在R上的奇函数,满足f(2﹣x)=f(x).若当0≤x≤1时,f(x)=2x﹣cos,则f(2019)= ﹣2 .
【解答】解:根据题意,f(x)是定义在R上的奇函数,则f(x)=﹣f(﹣x),
又由f(x)满足f(2﹣x)=f(x),则有f(2﹣x)=﹣f(﹣x),即f(x+2)=﹣f(x),
变形可得:f(x+4)=﹣f(x+2)=f(x),即函数f(x)是周期为4的周期函数,
则f(2019)=f(2020﹣1)=f(﹣1)=﹣f(1),
若当0≤x≤1时,f(x)=2x﹣cos,则f(1)=2﹣cos2,
则有f(2019)=﹣2;
故答案为:﹣2.
9.若,,则cos2α= .
【解答】解:若,,则sin(α)
则cos2α=sin(2α)=2sin(α)cos(α),
故答案为:.
10.如图,在平面四边形ABCD中,,AD=2,AB=BC=CA=4,E,F分别为边BC,CD的中点,则 .
【解答】解:如图所示,
∵E为BC中点,
∴,
同理,
∴??,
其中∠BAD=150°,∠BAC=60°,∠CAD=90°,
∴,,
,,
∴.
故答案为:.
11.在平面直角坐标系xOy中,点A在曲线y=x3上,该曲线在点A处的切线l与x轴交于点B.若AC⊥x轴,垂足为C,且BC长为1,则切线l的斜率为 27 .
【解答】解:由题意,设点A坐标为(x0,y0).
∵y′=3x2,∴y′|x=x0=3.
故曲线在点A处的切线l的斜率k=3.
∵y0,
∴切线l的直线方程为y3?(x﹣x0),
整理,得:y=3?x﹣2.
由题意知,B点坐标为(,0),C点坐标为(x0,0).
∴x01,解得x0=3.
∴切线l的斜率k=327.
故答案为:27.
12.已知函数则不等式f(x+2)>f(x)的解集是 (﹣∞,0)∪(3,+∞) .
【解答】解:若x>1,由f(x+2)>f(x)得(x+2)2﹣8(x+2)+8>x2﹣8x+8,
即4x>12,x>3,此时x>3成立,
若x+2≤1,即x≤﹣1时,由f(x+2)>f(x)得5(x+2)﹣4>5x﹣4,
得10>0,成立,此时x≤﹣1,
若﹣1<x≤1,则由f(x+2)>f(x)得(x+2)2﹣8(x+2)+8>5x﹣4,
即x2﹣9x>0,得x>9或x<0,
此时﹣1<x<0,
综上x<0或x>3,
即不等式的解集为(﹣∞,0)∪(3,+∞),
故答案为:(﹣∞,0)∪(3,+∞)
13.若函数f(x)=ax﹣x3(a>0,a≠1)有两个不同的零点,则a的取值范围是 .
【解答】解:∵f(x)=ax﹣x3(a>0,a≠1)有两个不同的零点,
∴等价于ax=x3恰有两个不同解.
当0<a<1,y=ax与y=﹣x3的图象只有一个交点,
不符合题意.
当a>1时,y=ax与y=﹣x3的图象在x∈(﹣∞,0)
上没有交点,
∴只考虑x>0,
于是两边取对数,得xlna=3lnx,即lna,
令g(x),则g′(x),
当x∈(0,e)时,g(x)单调递增,
当x<1时,g(x)<0,
x∈(e,+∞)时,g(x)单调递减且g(x)>0.
∴要有两个交点,0<lna<g(e),即1<a.
故答案为.
14.如图,在△ABC中,D,E是BC上的两个三等分点,,则cosB的最小值为 .
【解答】解:∵,
∴,
∴,
∴,
∴,
∴,
∴,
∴,
∴在△ABC中,2c2=4b2+bccos∠BAC,
∴2c2=4b2+bc,
∴b2,
∴cosB(当且仅当时,取“=”),
故cosB的最小值是:.
故答案为:.
二、解答题:本大题共10小题,共90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
15.如图,在四棱锥P﹣ABCD中,底面ABCD是平行四边形,E为棱PD的中点,平面PAB⊥底面ABCD,∠PAB=90°.求证:
(1)PB∥平面AEC;
(2)平面PAC⊥平面ABCD.
【解答】证明:(1)连BD,交AC于点O,连OE.因为底面ABCD是平行四边形,所以O为BD的中点.
因为E为棱PD的中点,所以OE∥PB,
又因为OE?平面AEC,PB?平面AEC,
所以PB∥平面AEC.
(2)因为平面PAB⊥底面ABCD,∠PAB=90°,
平面PAB∩平面ABCD=AB,PA?平面PAB,
所以PA⊥平面ABCD,
因为PA?平面PAC,
所以平面PAC⊥平面ABCD.
16.已知,(sinx,1),.
(1)若||,求cos2x的值;
(2)求函数f(x)?的单调区间和值域.
【解答】解:(1)因为,所以,
即,
所以.
因为,
所以,
因为,
所以,
所以.
所以.
(2)因为,
因为,所以x∈[,0],
当x∈[,]时,即时,f(x)单调递减;
当,
即时,f(x)单调递增;
故函数f(x)的单调增区间,单调减区间.
由于∈[﹣1,0],所以函数f(x)的值域为[﹣1,0].
17.已知函数f(x)=ax+bx(a>0,a≠1,b>0,b≠1)是偶函数.
(1)求ab的值;
(2)若f(lgx)<f(1),求x的取值范围.
【解答】解:(1)因为f(x)是偶函数,所以对任意实数x,有f(x)﹣f(﹣x)=0
即,
所以(axbx﹣1)(ax+bx)=0对任意实数x成立,
因为ax>0,bx>0,
所以axbx﹣1=0,即(ab)x=1对任意实数x成立,
所以ab=1.
(2)由(1)知,此时,
因为a>0,a≠1,b>0,b≠1,故不妨设a>1,
任取0≤x1<x2,
则,
因为0≤x1<x2,a>1,所以,
所以,,
所以f(x1)﹣f(x2)<0,
即f(x1)<f(x2),
所以f(x)在[0,+∞)上单调递增,
因为f(lg x)<f(1),
所以f(|lgx|)<f(1),
所以|lgx|<1,解得.
即不等式的解集为(,10).
18.如图,某登山队在山脚A处测得山顶B的仰角为45°,沿倾斜角为α(其中tanα)的斜坡前进km后到达D处,休息后继续行驶km到达山顶B.
(1)求山的高度BE;
(2)现山顶处有一塔CBkm.从A到D的登山途中,队员在点P处测得塔的视角为θ(∠CPB=θ).若点P处高度PF为xkm,则x为何值时,视角θ最大?
【解答】解:(1)方法一:因为,α是锐角,所以,,
所以;
在△ABD中,过D作DM⊥AB,垂足为M,
如图1所示;
因为,
所以;
在△ABE中,BE=ABcos45°=3,
所以山的高度为3 km.
方法二:过D作DG⊥AE于点G,过D作DH⊥BE于点H,如图2所示;
在△ADG中,∠DAG=α,,所以,,
所以,;
设BE=h,在直角△BDH中,BH=h﹣1,DH=h﹣2,
由于BD2=BH2+DH2,所以,
因为h>0,所以h=3;
所以山的高度为3 km.
(2)过P作PN⊥BE于N,如图3所示;
因为PF=x,所以AF=2x,
因为P在AD上,DG=1,所以x∈[0,1],
所以tan∠BPN,tan∠CPN,
所以tanθ=tan(∠CPN﹣∠BPN),x∈[0,1];
令t=3﹣2x∈[1,3],所以,
则tanθ,
当且仅当,即时,即时tanθ取得最大值.
所以,当km时,视角θ最大.
19.已知函数f(x)(a∈R).
(1)当a=0时,求f(x)的极值;
(2)若f(x)在区间(0,2)内有两个极值点,求实数a的取值范围.
【解答】解:(1)因为a=0,所以f(x),
所以f′(x),令f'(x)=0得x=2.列表如下.
x (0,2) 2 (2,+∞)
f′(x) ﹣ 0 +
f(x) ↘ 极小值f(2) ↗
因此,当x=2时,f(x)有极小值f(2)=ln2+1,无极大值;
(2)因为f′(x),
由0<x<2,得,
记g(x)=x﹣aex,x∈(0,2),
因为f(x)在区间(0,2)内有两个极值点,
所以g(x)在区间(0,2)内有两个零点,
所以g'(x)=1﹣aex且a>0,
令g'(x)=0,则x=﹣lna,
①当﹣lna≤0,即a≥1时,g'(x)<0,
所以g(x)在(0,2)上单调递减,至多与x轴有一个交点,不满足题意;
②当﹣ln a≥2,即0<a时,g'(x)>0,
所以g(x)在(0,2)上单调递增,至多与x轴有一个交点,不满足题意;
③当0<﹣ln a<2,即时,g(x)在(0,﹣ln a)上单调递增,
在(﹣ln a,2)上单调递减;
由g(0)=﹣a<0,要使g(x)在区间(0,2)内有两个零点,
必须满足解得,
综上所述,实数a的取值范围是.
20.数列{an}的各项均为正数,其前n项和为Sn.已知对任意的n∈N*,存在实数p,q满足.
(1)若an=2n,求p,q的值;
(2)若a1,a2,a3成等差数列,求证:数列{an}是等差数列.
【解答】(1)解:∵an=2n,∴数列{an}是首项为2,公差为2的等差数列,
∴,
代入得,n2+n=4pn2+qn,
∵上式对n∈N*恒成立,∴,
故;
(2)证明:∵a1,a2,a3成等差数列,设公差为d≥0,
则,即 ,
②﹣①×2,③﹣①×3得,,
⑤﹣④×3得,,∴p=0或a1=d,
1°当p=0时,Sn=qn,∴an=q,
∴an+1﹣an=0,
∴{an}是以q为首项,0为公差的等差数列.
2°当a1=d时,则d>0,代入④,①得,,,
∴,,
两式相减得,,
得,
∴an+1+an=d或an+1﹣an=d,
∵a1=d>0,a1,a2,a3成等差数列,
∴a2=2d,a3=3d,下面证明an+1﹣an=d对n∈N*恒成立,
假设an+1+an=d成立的最小n值为k,即ak+1+ak=d,显然k≥3,
又ak﹣ak﹣1=d,
两式相减得,ak+1+ak﹣1=0,这与an>0,n∈N*矛盾,
因此,an+1﹣an=d,n∈N*,
∴{an}是以d为首项d为公差的等差数列.
综合1°2°,数列{an}是等差数列.
21.在空间直角坐标系O﹣xyz中,O(0,0,0),A(1,0,0),B(1,2,0),C(0,1,2),点P满足.
(1)求点P的坐标(用λ表示);
(2)若OP⊥BC,求λ的值.
【解答】解:(1)因为A(1,0,0),C(0,1,2),
所以,
因为,
所以,
所以点P的坐标为(1﹣λ,λ,2λ).
(2)因为,OP⊥BC,
所以,即﹣1×(1﹣λ)﹣1×λ+2×2λ=0,
解得.
22.确定函数f(x)=cos2x+4cosx,x∈(0,2π)的单调区间.
【解答】解:函数的导数f'(x)=﹣2sin2x﹣4sinx=﹣4sinx(cosx+1),
令f'(x)>0,sinx<0,
又x∈(0,2π),所以π<x<2π;
令f'(x)<0,sinx>0,
又x∈(0,2π),所以0<x<π.
故f(x)的单调增区间为(π,2π),单调减区间为(0,π).
23.在直四棱柱ABCD﹣A1B1C1D1中,AB⊥AC,AB=1,AC=AA1=2,.
(1)求二面角D1﹣AC﹣B1的余弦值;
(2)试问线段A1B1上是否存在点E,使得直线DE∥平面ACB1?若存在,求线段A1E的长;若不存在,说明理由.
【解答】解:(1)在直四棱柱ABCD﹣A1B1C1D1中,AA1⊥平面ABCD,
因为AB?平面ABCD,AC?平面ABCD,所以AA1⊥AB,AA1⊥AC,
因为AB⊥AC,所以以A为坐标原点,AC,AB,AA1分别为x,y,z轴建立空间直角坐标系,
如图所示.
依题意可得A(0,0,0),B(0,1,0),C(2,0,0),D(1,﹣2,0),
A1(0,0,2),B1(0,1,2),C1(2,0,2),D1(1,﹣2,2).
设为平面ACB1的法向量,则
因为,所以
不妨设z=1,可得.
设为平面ACD1的法向量,则
因为,所以
不妨设z=1,可得.
所以.
由图知,二面角D1﹣AC﹣B1为锐角,
所以二面角D1﹣AC﹣B1的余弦值为.
(2)假设线段A1B1上是否存在点E,使得直线DE∥平面ACB1,则,
设A1E=a,0≤a≤1,则E(0,a,2),.
所以,
所以a=﹣1,不合题意,故舍去.
所以,线段A1B1上不存在点E,使直线DE∥平面ACB1.
24.已知x>1,,,n∈N*.
(1)比较S2(x)与T2(x)的大小;
(2)比较Sn(x)与Tn(x)(n∈N*)大小,并加以证明.
【解答】解:(1)S2(x)﹣T2(x)
,
因为x>1,所以,
所以S2(x)﹣T2(x)<0,所以S2(x)<T2(x);
(2)本题结论为Sn(x)≤Tn(x),n∈N*,证明如下:
要证Sn(x)≤Tn(x),n∈N*,只要证,n∈N*,
只要证,n∈N*,
因为x>1,所以只要证,n∈N*,(*)
下面用数学归纳法证明:
①当n=1时,(*)式成立.
②假设当n=k时,(*)式成立,即有,
则当n=k+1时,(*)式左边,
而此时(*)式右边,
所以只要证,
只要证kxk+1﹣(k+1)xk+1≥0,(**)
令f(x)=kxk+1﹣(k+1)xk+1,x>1,k∈N*,
因为f'(x)=k(k+1)xk﹣k(k+1)xk﹣1=k(k+1)xk﹣1(x﹣1)>0,
所以f(x)在(1,+∞)上单调递增,所以f(x)>f(1)=0,
故(**)式成立.这就是说,当n=k+1时,(*)式也成立,
综合①②可知(*)式成立,
所以Sn(x)≤Tn(x),n∈N*成立,得证.
同课章节目录
