2019年八年级物理沪科版第五章质量与密度(35张ppt)
文档属性
| 名称 | 2019年八年级物理沪科版第五章质量与密度(35张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2019-12-09 09:34:56 | ||
图片预览








文档简介
课件35张PPT。质量和密度
复习复习目标:
1:理解质量是物质的一种属性,不随物质的形状、状态、
位置的变化而变化。
2.能熟练运用天平测量固体、液体的质量。
3.理解密度的相关知识(定义、公式、单位及单位间的
换算等)。
4.能对固体和液体的密度进行测定。
5.能运用密度知识解决实际问题。想一想这一章我们需要复习什么呢?质量定义:物体中所含物质的多少叫做质量。质量是物体的一种 ,它不随物体的 、 和
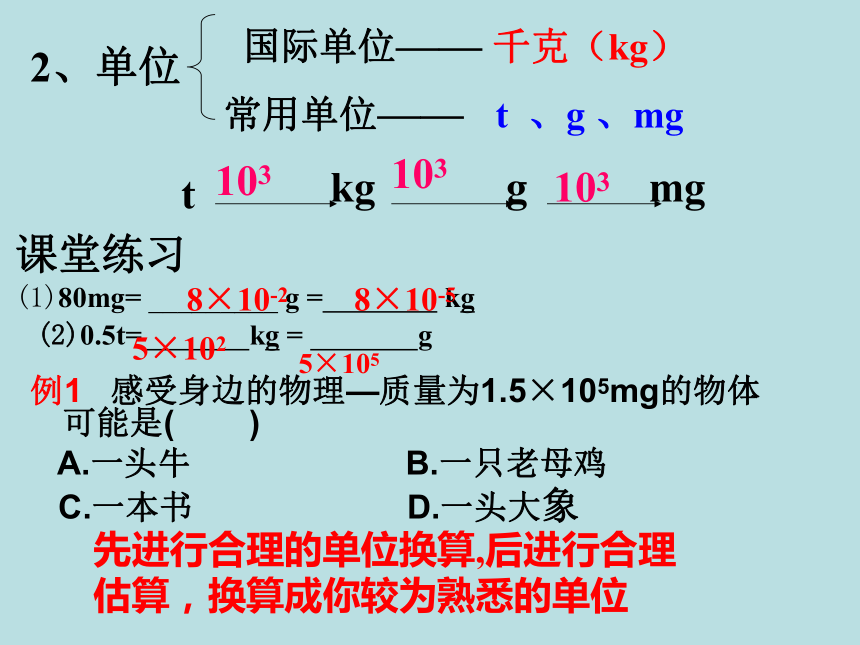
而改变。单位及换算:Kg(国际单位)质量的测量:测量工具天平的结构与使用知识网络属性t、g、mg1、2kg的铁块完全熔化为铁水,其质为 。当这铁水全部浇铸成一铁球,其质量为 。将这铁球带到月球上时,其质量为 。以上现象说明了什么?质量是物体本身的一种基本属性。它不随物体的形状、状态、位置的改变而改变。2、单位国际单位—— 千克(kg)常用单位—— t 、g 、mg课堂练习
(1)80mg= _________ g = kg
(2)0.5t= kg = g 8×10-28×10-55×1025×105
例1 感受身边的物理—质量为1.5×105mg的物体可能是( )
A.一头牛 B.一只老母鸡
C.一本书 D.一头大象
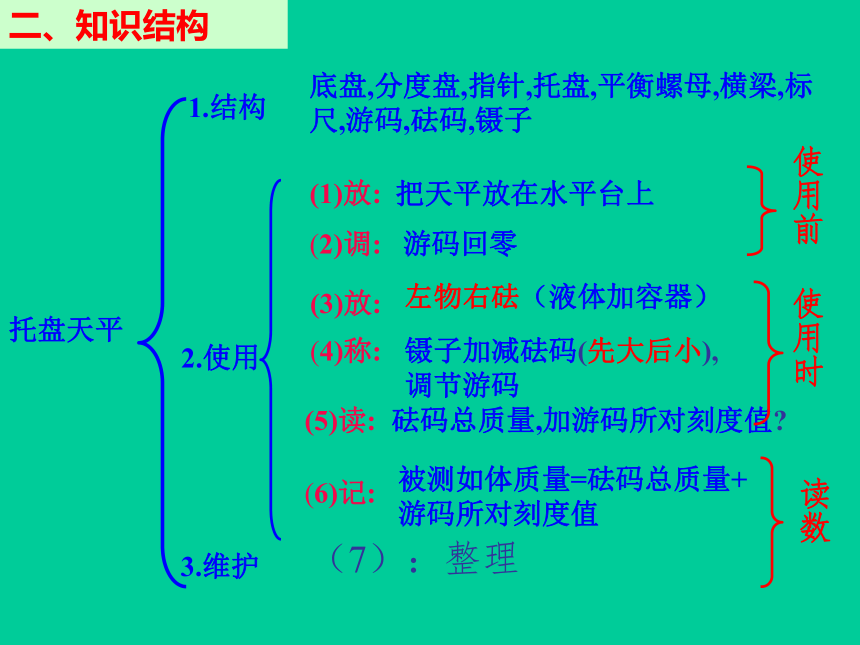
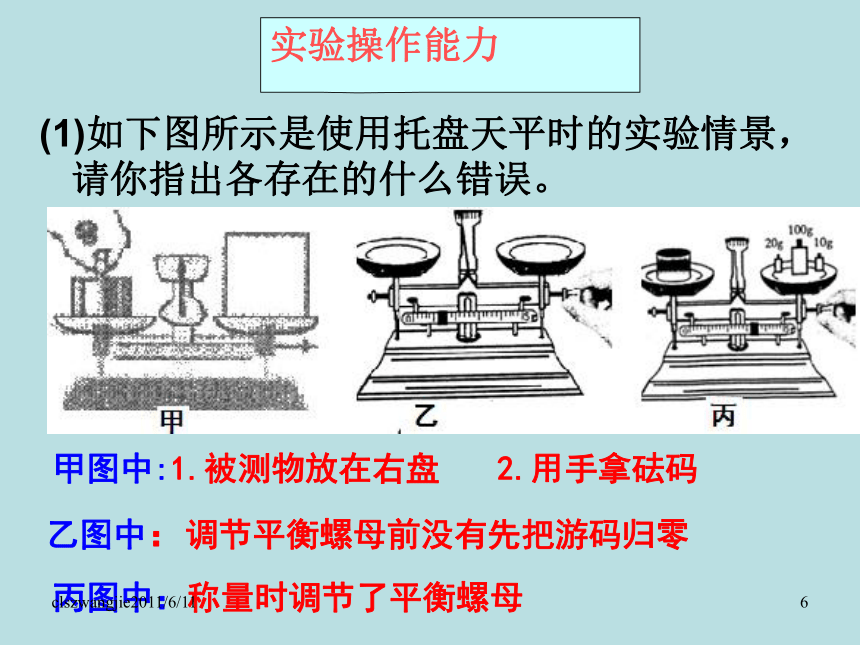
先进行合理的单位换算,后进行合理估算,换算成你较为熟悉的单位二、知识结构托盘天平1.结构底盘,分度盘,指针,托盘,平衡螺母,横梁,标尺,游码,砝码,镊子2.使用(1)放:把天平放在水平台上(2)调:游码回零(3)放:左物右砝(液体加容器)(4)称:镊子加减砝码(先大后小),调节游码(5)读:砝码总质量,加游码所对刻度值?(6)记:被测如体质量=砝码总质量+游码所对刻度值3.维护使用前使用时读数(7):整理(1)如下图所示是使用托盘天平时的实验情景,请你指出各存在的什么错误。
甲图中:1.被测物放在右盘 2.用手拿砝码
丙图中:称量时调节了平衡螺母乙图中:调节平衡螺母前没有先把游码归零实验操作能力
clszwangjie2011/6/116例1.若在调节天平时游码没有放在零刻线处,用这架天平称量物体时,称量结果将比物体质 量的真实值_____. 若调节平衡的天平使用已磨损的砝码称量时,测量结果 将比物体质量的真实值______.(填“偏大”或“偏小”)
关于天平的误差分析可用天平的简易图来分析偏大偏大密度1:定义:单位体积某种物质的质量叫做这种物质的密度。密度的测定:3:密度知识的应用:密度是物质的一种 。它决定于物质的 。国际单位:如何测定固体的密度。求质量(m=ρV)鉴别物质求体积( )知识网络特性种类和状态等如何测定液体的密度。原理器材常用单位:kg/m3g/cm31g/cm3=1×103kg/m3 2、密度计算公式:
4.水的密度为:
ρ水=1.0 ? 10 3 kg/m3
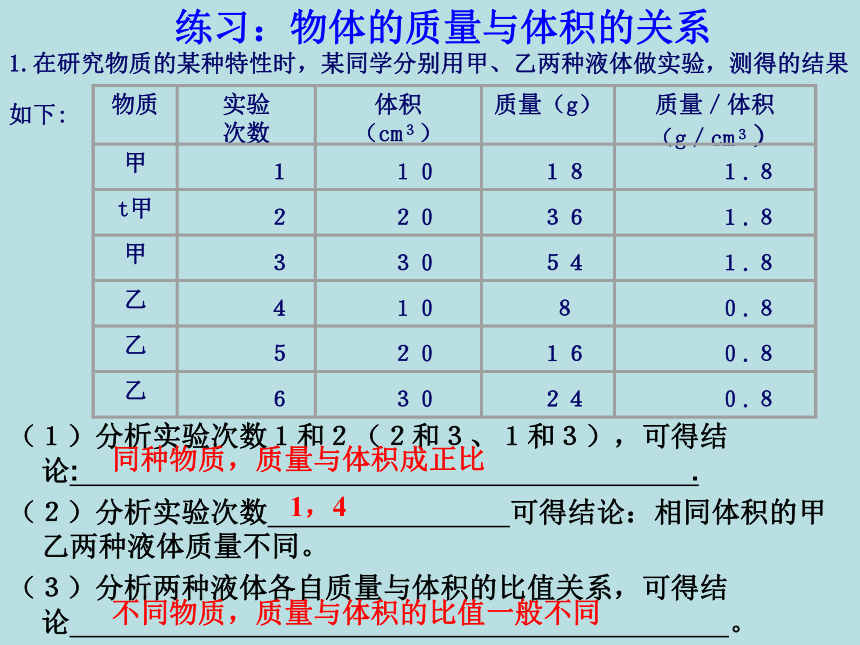
物理意义:1立方米的水质量为1.0 ? 10 3千克1.在研究物质的某种特性时,某同学分别用甲、乙两种液体做实验,测得的结果如下: (1)分析实验次数1和2(2和3、1和3),可得结论: .
(2)分析实验次数 可得结论:相同体积的甲乙两种液体质量不同。
(3)分析两种液体各自质量与体积的比值关系,可得结论 。 练习:物体的质量与体积的关系同种物质,质量与体积成正比1,4不同物质,质量与体积的比值一般不同类型题总结(一)、密度概念的理解 1、根据公式ρ=m/V,对于同种物质,下面说法正确的是( )
A、ρ与m成正比 B、ρ与V成反比
C、ρ与m成正比,与V成反比 D、ρ与m、V无关2.工人使用氧气瓶内的氧气进行气焊的过程中,以下有关瓶内氧气的物理量中,不变的是 ( )
A.质量 B.体积 C.密度 D.以上都是DB例1. 关于密度公式 的说法中正确的是( )
A.物质的密度跟它的质量成正比
B.物质的密度跟它的体积成反比
C.物质的密度跟它的质量成正比,且跟它的体积成反比
D.物质密度跟它的质量、体积大小无关2.典型例题分析D密度是物质的一种特性,同种物质密度一般相同,跟物体的质量和体积均无关,公式是定义密度的公式,是测量密度大小的公式,而不是决定密度大小的公式。密度的理解
clszwangjie2011/6/1111四.密度的应用
①鉴别物质: ②求质量 :
③求体积:
④判断物体实心还是空心:m=ρV12冰的密度是0.9×103 kg/m3.一块体积为100 cm3的冰熔化成水后, 质量是____g,体积是____cm3. 135 g的水结成冰后,质量是_____kg,体积是_____cm3.
一:质量相等问题 例1:一个瓶子能盛500克水,用这个瓶子能盛多少克酒精?二:体积相等问题2、最多只能装1kg酒精的瓶子,一定不能装下1kg的( )(ρ水银>ρ盐水>ρ水>ρ酒精>ρ汽油)
A、水 B、汽油 C、水银 D、盐水 1、质量和体积都相等的铁球、铅球和铜
球(ρ铅>ρ铜>ρ铁),下列说法正确的是( )
A、若铁球空心,则铜球、铅球一定空心
B、若铅球空心,则铜球、铁球一定空心
C、若铜球空心,则铅球、铁球一定空心
D、三个球都可能实心
三:空心、实心问题3.一个质量为200克的瓶子,装满酒精后总质量为680克,这个瓶子若装满水,总质量是多少克?( 酒 = 0.8×103kg/m3 )2.三个质量体积都相同的铝球、铁球和铜球,下面说法正确的是( )
A.可能都是实心的 B.可能都是空心的
C.铝球可能实心的 D.铜球的空心部分最大答案:800克答案: BCD例2.质量相等体积相同的空心铜球、铁球和铝球各一个(ρ铜> ρ铁> ρ铝),则空心部分体积最大的球是 ( )
A.铜球 B.铁球
C.铝球 D.条件不足无法确定原理:天平砝码量筒待测物烧杯、水盐水细线实验:测定固体和液体的密度目的:用天平和量筒测定固体和液体的密度 ρ= m / v器材:三.用天平和量筒测量物质的密度
(1)实验原理:
(2)质量的测量:用天平 可直接测量 的质量,间接测量液体质量。
(3)体积的测量:用 可直接测量液体的体积,间接测量固体的体积。知识梳理固体量筒凹面底部读数方法:
视线应与液面
的 相平先弄清分度值再度数
clszwangjie2011/6/11171.如何测固体(如小石块)的密度1. 。2. 。3. 。小石块 参照上面的三幅图,请叙述测石块密度的步骤,设计出记录数据的表格,写出密度的表达式。用天平测出石块的质量m用量筒测出水的体积V1将石块放入量筒中,测出水和石块的总体积V2ρ固=4、密度的测量(1)测量石块的密度步骤①将天平放在水平桌面上,调节天平平衡
②用天平测出石块的质量m
③向量筒中注入适量的清水,并把测得水的体积为v1
④将石块用细线拴好,完全浸没在水中,测出金属块和水得总体积为v2
⑤计算石块得体积v = v2 — v1
⑥计算出石块的密度ρ= m/v2 — v1
(2)美术课上同学们用橡皮泥捏动物模型时,想知道橡皮泥的密度有多大。课后,他们在实验室选择了天平、量筒、水和细线进行了实验操作。①合理的操作顺序是(填号): 。
②由图可知:橡皮泥的质量m = g; 橡皮泥的体积V= cm3;
橡皮泥的密度ρ= 。C、A、B13.410 1.34×103kg/m3 或 1.34g/cm3测定固体密度的方法3.考点训练clszwangjie2011/6/1120例1.张华拾到一个小金属零件,就把它带回学校利用天平和量筒来测定这个零件的密度.具体操作如下:
①把天平放在 上,并将游码移至标尺的零刻线处;调节天平横梁平衡时,发现指针位置如图甲所示,此时应将平衡螺母向 (填“左”或“右”)调节
②用调节好的天平测零件的质量.天平平衡时, 砝码的质量及游码在标尺上的位置如图乙所示,则零件的质量为 g,用量筒测得零件的体积如图丙所示,则零件的体积为 cm3,由此可算得小金属零件的密度为 g/cm3.
③若该零件磨损后,它的质量将 ,密度将 (填“变大”、“变小” 或“不变”).右62203.1水平面变小不变测固体密度2.典型例题分析clszwangjie2011/6/1121【扩展】如何测小蜡块、盐块、糖块(密度比水小)的体积?针压法(上压法) 悬重法(下拉法)“排水法”测体积ρ物> ρ水ρ物< ρ水测定盐水的密度3.如何测液体(如盐水)的密度1. 。2. 。3. 。用天平测出烧杯和盐水的总质量m1将一部分盐水倒入量筒中,读出量筒中盐水的体积V 用天平测出烧杯和剩余盐水的质量m2 上面的三幅图是常规的实验方案,请将下面的步骤补充完整,并练习设计出记录数据的表格。ρ液=(2)测量液体的密度步骤①调节天平平衡
②在烧杯中盛被测液体,用天平测出质量为 m1
③把烧杯中的被测液体倒入量筒中一部分,测出它的体积为v
④用天平测出烧杯和杯中剩余液体的质量m2
⑤计算出量筒内液体的质量m = m1— m2
⑥求出液体的密度ρ =(m1 — m2 )∕ v
m2m1m=m1-m2例已知: 求: 戒指的密度 解: 1、计算物质的密度: ρ=m/V 自然界是由各种各样的物质组成的,不同物质有不同的特性,人们正是根据物质的这些特性来区分、鉴别不同的物质.二、密度知识的应用某一戒指质量为8.8克,体积为0.55厘米3,你能鉴别一下这个戒指是纯金的吗?m = 8.8g V= 0.55cm3 =16g/cm3答:查密度表纯金的密度是19.3g/cm3,16<19.3,戒指不是纯金的。2、计算物体的质量: m=ρV人民英雄纪念碑的碑心石是体积为42.6米3的一整块花岗岩,花岗岩的密度是2.8×103千克/米3,碑心石的质量是多少?解:由公式ρ=m/v得
m=ρV= 2.8×103kg/m3 ×42.6m3= 119×103kg=119t
答:碑心石的质量是119t。可以计算质量难以测量的物体的质量
(如金字塔、人民英雄纪念碑等)例3、计算物体的体积: V=m/ ρ用天平称得一捆细铜丝的质量是445克,已知铜的密度是8.9×103千克/米3,这捆细铜丝的体积是多少?可以计算一些体积难以测量的物体的体积
(如沙子、等一些形状不规则的物体)解:由公式ρ=m/v得
v= m/ρ=445g/8.9g/cm3= 50cm3注:如果知道铜丝的横截面积我们还可以计算出这捆铜丝的长度。例 =12.5g/cm3
=12.5×103 kg/m3< 19.3×103kg/m3
解:答:这枚金牌可能是空心的,也可能不是纯金的判断物体是否实心可有多种方法:方法一:比较密度法例2.有一枚体育运动会颁发的金牌,先用天平称得它的质量为25g,再用量筒测得其体积为2cm3。通过有关计算说明这枚金牌是否是空心的。(纯金密度是19.3×103kg/m3)clszwangjie2011/6/1129 假定物体是实心的,计算2cm3的金质量是 ,
判定该铝球是空心的。 质量是25g的实心金币球计算体积应是
= 1.3cm3,
因为1.3cm3<2cm3,判定该铝球是空心的。m=ρV= 19.3g/cm3×2cm3=38.6 g,
因为38.6g< 25g方法三:比较体积法方法二:比较质量法305、会用比例关系解密度问题 (1)同一种物质,密度相同,体积大的质量也大,物质的质量跟它的体积成正比。即:
ρ一定,(2)不同的物质,密度不同,在体积相同的情况下,密度大的质量也大,物质的质量跟它的密度成正比。即:
当V一定时 ,(3)不同的物质,密度不同,在质量相同的情况下,密度大的体积反而小。物体的体积跟它的密度成反比,即:
当m一定时, 应用密度公式的比例计算1、甲乙两个物体的质量之比为3︰7,体积之比为2︰5,则甲乙的密度之比为_______.
2、甲乙两物体是由同种材料制成的,体积之比为9︰7,则质量之M乙︰M甲=_________.15︰147︰92、如图5所示是A、B、C三种物质的质量m与体积V的关系图线。由图可知,A、B、C三种物质的密度ρA、ρB、ρC之间的大小关系是 ( )
A.ρA<ρB<ρC B.ρA<ρB>ρC
C.ρA>ρB>ρC D.ρA>ρB<ρCA(2).如下图所示是A、B两种物质的质量m与体积V的关系图, 由图可知,A、B两种物质的密度ρA、ρB和水的密度ρ水之间的关系是 ( )
ρA>ρB>ρ水
B. ρB>ρA> ρ水
C. ρA>ρ水>ρB
D. ρ水>ρA>ρB3.考点训练Cρ水 利用图象比较物质的密度,注意控制变量读图能力当密度相同时,物体的质量与体积成正比
当体积相同时,物体的质量与密度成正比,
当质量相同时,物体的体积与密度成反比
343.一个瓶子能盛1kg水,用这个瓶子能盛多少kg煤油?已知:求:解:m水=1kg, V水=V煤油, ρ水=1000kg/m3,ρ煤油=800kg/m3 m煤油 4.一个瓶子能装下1kg的水,用这个瓶子能装下1kg的
A.汽油 B.酒精 C.水银 D.盐水当V一定时 ,m煤=0.8kg当V一定时 ,密度大的质量大C、D
复习复习目标:
1:理解质量是物质的一种属性,不随物质的形状、状态、
位置的变化而变化。
2.能熟练运用天平测量固体、液体的质量。
3.理解密度的相关知识(定义、公式、单位及单位间的
换算等)。
4.能对固体和液体的密度进行测定。
5.能运用密度知识解决实际问题。想一想这一章我们需要复习什么呢?质量定义:物体中所含物质的多少叫做质量。质量是物体的一种 ,它不随物体的 、 和
而改变。单位及换算:Kg(国际单位)质量的测量:测量工具天平的结构与使用知识网络属性t、g、mg1、2kg的铁块完全熔化为铁水,其质为 。当这铁水全部浇铸成一铁球,其质量为 。将这铁球带到月球上时,其质量为 。以上现象说明了什么?质量是物体本身的一种基本属性。它不随物体的形状、状态、位置的改变而改变。2、单位国际单位—— 千克(kg)常用单位—— t 、g 、mg课堂练习
(1)80mg= _________ g = kg
(2)0.5t= kg = g 8×10-28×10-55×1025×105
例1 感受身边的物理—质量为1.5×105mg的物体可能是( )
A.一头牛 B.一只老母鸡
C.一本书 D.一头大象
先进行合理的单位换算,后进行合理估算,换算成你较为熟悉的单位二、知识结构托盘天平1.结构底盘,分度盘,指针,托盘,平衡螺母,横梁,标尺,游码,砝码,镊子2.使用(1)放:把天平放在水平台上(2)调:游码回零(3)放:左物右砝(液体加容器)(4)称:镊子加减砝码(先大后小),调节游码(5)读:砝码总质量,加游码所对刻度值?(6)记:被测如体质量=砝码总质量+游码所对刻度值3.维护使用前使用时读数(7):整理(1)如下图所示是使用托盘天平时的实验情景,请你指出各存在的什么错误。
甲图中:1.被测物放在右盘 2.用手拿砝码
丙图中:称量时调节了平衡螺母乙图中:调节平衡螺母前没有先把游码归零实验操作能力
clszwangjie2011/6/116例1.若在调节天平时游码没有放在零刻线处,用这架天平称量物体时,称量结果将比物体质 量的真实值_____. 若调节平衡的天平使用已磨损的砝码称量时,测量结果 将比物体质量的真实值______.(填“偏大”或“偏小”)
关于天平的误差分析可用天平的简易图来分析偏大偏大密度1:定义:单位体积某种物质的质量叫做这种物质的密度。密度的测定:3:密度知识的应用:密度是物质的一种 。它决定于物质的 。国际单位:如何测定固体的密度。求质量(m=ρV)鉴别物质求体积( )知识网络特性种类和状态等如何测定液体的密度。原理器材常用单位:kg/m3g/cm31g/cm3=1×103kg/m3 2、密度计算公式:
4.水的密度为:
ρ水=1.0 ? 10 3 kg/m3
物理意义:1立方米的水质量为1.0 ? 10 3千克1.在研究物质的某种特性时,某同学分别用甲、乙两种液体做实验,测得的结果如下: (1)分析实验次数1和2(2和3、1和3),可得结论: .
(2)分析实验次数 可得结论:相同体积的甲乙两种液体质量不同。
(3)分析两种液体各自质量与体积的比值关系,可得结论 。 练习:物体的质量与体积的关系同种物质,质量与体积成正比1,4不同物质,质量与体积的比值一般不同类型题总结(一)、密度概念的理解 1、根据公式ρ=m/V,对于同种物质,下面说法正确的是( )
A、ρ与m成正比 B、ρ与V成反比
C、ρ与m成正比,与V成反比 D、ρ与m、V无关2.工人使用氧气瓶内的氧气进行气焊的过程中,以下有关瓶内氧气的物理量中,不变的是 ( )
A.质量 B.体积 C.密度 D.以上都是DB例1. 关于密度公式 的说法中正确的是( )
A.物质的密度跟它的质量成正比
B.物质的密度跟它的体积成反比
C.物质的密度跟它的质量成正比,且跟它的体积成反比
D.物质密度跟它的质量、体积大小无关2.典型例题分析D密度是物质的一种特性,同种物质密度一般相同,跟物体的质量和体积均无关,公式是定义密度的公式,是测量密度大小的公式,而不是决定密度大小的公式。密度的理解
clszwangjie2011/6/1111四.密度的应用
①鉴别物质: ②求质量 :
③求体积:
④判断物体实心还是空心:m=ρV12冰的密度是0.9×103 kg/m3.一块体积为100 cm3的冰熔化成水后, 质量是____g,体积是____cm3. 135 g的水结成冰后,质量是_____kg,体积是_____cm3.
一:质量相等问题 例1:一个瓶子能盛500克水,用这个瓶子能盛多少克酒精?二:体积相等问题2、最多只能装1kg酒精的瓶子,一定不能装下1kg的( )(ρ水银>ρ盐水>ρ水>ρ酒精>ρ汽油)
A、水 B、汽油 C、水银 D、盐水 1、质量和体积都相等的铁球、铅球和铜
球(ρ铅>ρ铜>ρ铁),下列说法正确的是( )
A、若铁球空心,则铜球、铅球一定空心
B、若铅球空心,则铜球、铁球一定空心
C、若铜球空心,则铅球、铁球一定空心
D、三个球都可能实心
三:空心、实心问题3.一个质量为200克的瓶子,装满酒精后总质量为680克,这个瓶子若装满水,总质量是多少克?( 酒 = 0.8×103kg/m3 )2.三个质量体积都相同的铝球、铁球和铜球,下面说法正确的是( )
A.可能都是实心的 B.可能都是空心的
C.铝球可能实心的 D.铜球的空心部分最大答案:800克答案: BCD例2.质量相等体积相同的空心铜球、铁球和铝球各一个(ρ铜> ρ铁> ρ铝),则空心部分体积最大的球是 ( )
A.铜球 B.铁球
C.铝球 D.条件不足无法确定原理:天平砝码量筒待测物烧杯、水盐水细线实验:测定固体和液体的密度目的:用天平和量筒测定固体和液体的密度 ρ= m / v器材:三.用天平和量筒测量物质的密度
(1)实验原理:
(2)质量的测量:用天平 可直接测量 的质量,间接测量液体质量。
(3)体积的测量:用 可直接测量液体的体积,间接测量固体的体积。知识梳理固体量筒凹面底部读数方法:
视线应与液面
的 相平先弄清分度值再度数
clszwangjie2011/6/11171.如何测固体(如小石块)的密度1. 。2. 。3. 。小石块 参照上面的三幅图,请叙述测石块密度的步骤,设计出记录数据的表格,写出密度的表达式。用天平测出石块的质量m用量筒测出水的体积V1将石块放入量筒中,测出水和石块的总体积V2ρ固=4、密度的测量(1)测量石块的密度步骤①将天平放在水平桌面上,调节天平平衡
②用天平测出石块的质量m
③向量筒中注入适量的清水,并把测得水的体积为v1
④将石块用细线拴好,完全浸没在水中,测出金属块和水得总体积为v2
⑤计算石块得体积v = v2 — v1
⑥计算出石块的密度ρ= m/v2 — v1
(2)美术课上同学们用橡皮泥捏动物模型时,想知道橡皮泥的密度有多大。课后,他们在实验室选择了天平、量筒、水和细线进行了实验操作。①合理的操作顺序是(填号): 。
②由图可知:橡皮泥的质量m = g; 橡皮泥的体积V= cm3;
橡皮泥的密度ρ= 。C、A、B13.410 1.34×103kg/m3 或 1.34g/cm3测定固体密度的方法3.考点训练clszwangjie2011/6/1120例1.张华拾到一个小金属零件,就把它带回学校利用天平和量筒来测定这个零件的密度.具体操作如下:
①把天平放在 上,并将游码移至标尺的零刻线处;调节天平横梁平衡时,发现指针位置如图甲所示,此时应将平衡螺母向 (填“左”或“右”)调节
②用调节好的天平测零件的质量.天平平衡时, 砝码的质量及游码在标尺上的位置如图乙所示,则零件的质量为 g,用量筒测得零件的体积如图丙所示,则零件的体积为 cm3,由此可算得小金属零件的密度为 g/cm3.
③若该零件磨损后,它的质量将 ,密度将 (填“变大”、“变小” 或“不变”).右62203.1水平面变小不变测固体密度2.典型例题分析clszwangjie2011/6/1121【扩展】如何测小蜡块、盐块、糖块(密度比水小)的体积?针压法(上压法) 悬重法(下拉法)“排水法”测体积ρ物> ρ水ρ物< ρ水测定盐水的密度3.如何测液体(如盐水)的密度1. 。2. 。3. 。用天平测出烧杯和盐水的总质量m1将一部分盐水倒入量筒中,读出量筒中盐水的体积V 用天平测出烧杯和剩余盐水的质量m2 上面的三幅图是常规的实验方案,请将下面的步骤补充完整,并练习设计出记录数据的表格。ρ液=(2)测量液体的密度步骤①调节天平平衡
②在烧杯中盛被测液体,用天平测出质量为 m1
③把烧杯中的被测液体倒入量筒中一部分,测出它的体积为v
④用天平测出烧杯和杯中剩余液体的质量m2
⑤计算出量筒内液体的质量m = m1— m2
⑥求出液体的密度ρ =(m1 — m2 )∕ v
m2m1m=m1-m2例已知: 求: 戒指的密度 解: 1、计算物质的密度: ρ=m/V 自然界是由各种各样的物质组成的,不同物质有不同的特性,人们正是根据物质的这些特性来区分、鉴别不同的物质.二、密度知识的应用某一戒指质量为8.8克,体积为0.55厘米3,你能鉴别一下这个戒指是纯金的吗?m = 8.8g V= 0.55cm3 =16g/cm3答:查密度表纯金的密度是19.3g/cm3,16<19.3,戒指不是纯金的。2、计算物体的质量: m=ρV人民英雄纪念碑的碑心石是体积为42.6米3的一整块花岗岩,花岗岩的密度是2.8×103千克/米3,碑心石的质量是多少?解:由公式ρ=m/v得
m=ρV= 2.8×103kg/m3 ×42.6m3= 119×103kg=119t
答:碑心石的质量是119t。可以计算质量难以测量的物体的质量
(如金字塔、人民英雄纪念碑等)例3、计算物体的体积: V=m/ ρ用天平称得一捆细铜丝的质量是445克,已知铜的密度是8.9×103千克/米3,这捆细铜丝的体积是多少?可以计算一些体积难以测量的物体的体积
(如沙子、等一些形状不规则的物体)解:由公式ρ=m/v得
v= m/ρ=445g/8.9g/cm3= 50cm3注:如果知道铜丝的横截面积我们还可以计算出这捆铜丝的长度。例 =12.5g/cm3
=12.5×103 kg/m3< 19.3×103kg/m3
解:答:这枚金牌可能是空心的,也可能不是纯金的判断物体是否实心可有多种方法:方法一:比较密度法例2.有一枚体育运动会颁发的金牌,先用天平称得它的质量为25g,再用量筒测得其体积为2cm3。通过有关计算说明这枚金牌是否是空心的。(纯金密度是19.3×103kg/m3)clszwangjie2011/6/1129 假定物体是实心的,计算2cm3的金质量是 ,
判定该铝球是空心的。 质量是25g的实心金币球计算体积应是
= 1.3cm3,
因为1.3cm3<2cm3,判定该铝球是空心的。m=ρV= 19.3g/cm3×2cm3=38.6 g,
因为38.6g< 25g方法三:比较体积法方法二:比较质量法305、会用比例关系解密度问题 (1)同一种物质,密度相同,体积大的质量也大,物质的质量跟它的体积成正比。即:
ρ一定,(2)不同的物质,密度不同,在体积相同的情况下,密度大的质量也大,物质的质量跟它的密度成正比。即:
当V一定时 ,(3)不同的物质,密度不同,在质量相同的情况下,密度大的体积反而小。物体的体积跟它的密度成反比,即:
当m一定时, 应用密度公式的比例计算1、甲乙两个物体的质量之比为3︰7,体积之比为2︰5,则甲乙的密度之比为_______.
2、甲乙两物体是由同种材料制成的,体积之比为9︰7,则质量之M乙︰M甲=_________.15︰147︰92、如图5所示是A、B、C三种物质的质量m与体积V的关系图线。由图可知,A、B、C三种物质的密度ρA、ρB、ρC之间的大小关系是 ( )
A.ρA<ρB<ρC B.ρA<ρB>ρC
C.ρA>ρB>ρC D.ρA>ρB<ρCA(2).如下图所示是A、B两种物质的质量m与体积V的关系图, 由图可知,A、B两种物质的密度ρA、ρB和水的密度ρ水之间的关系是 ( )
ρA>ρB>ρ水
B. ρB>ρA> ρ水
C. ρA>ρ水>ρB
D. ρ水>ρA>ρB3.考点训练Cρ水 利用图象比较物质的密度,注意控制变量读图能力当密度相同时,物体的质量与体积成正比
当体积相同时,物体的质量与密度成正比,
当质量相同时,物体的体积与密度成反比
343.一个瓶子能盛1kg水,用这个瓶子能盛多少kg煤油?已知:求:解:m水=1kg, V水=V煤油, ρ水=1000kg/m3,ρ煤油=800kg/m3 m煤油 4.一个瓶子能装下1kg的水,用这个瓶子能装下1kg的
A.汽油 B.酒精 C.水银 D.盐水当V一定时 ,m煤=0.8kg当V一定时 ,密度大的质量大C、D
同课章节目录
- 第一章 打开物理世界的大门
- 第一节 走进神奇
- 第二节 探索之路
- 第三节 站在巨人的肩膀上
- 第二章 运动的世界
- 第一节 动与静
- 第二节 长度与时间的测量
- 第三节 快与慢
- 第四节 科学探究:速度的变化
- 第三章 声的世界
- 第一节 科学探究:声音的产生与传播
- 第二节 声音的特性
- 第三节 超声与次声
- 第四章 多彩的光
- 第一节 光的反射
- 第二节 平面镜成像
- 第三节 光的折射
- 第四节 光的色散
- 第五节 科学探究:凸透镜成像
- 第六节 神奇的眼睛
- 第五章 质量与密度
- 第一节 质量
- 第二节 学习使用天平和量筒
- 第三节 科学探究:物质的密度
- 第四节 密度知识的应用
- 第六章 熟悉而陌生的力
- 第一节 力
- 第二节 怎样描述力
- 第三节 弹力与弹簧测力计
- 第四节 来自地球的力
- 第五节 科学探究:摩擦力
- 第七章 力与运动
- 第一节 科学探究:牛顿第一定律
- 第二节 力的合成
- 第三节 力的平衡
- 第八章 压强
- 第一节 压力的作用效果
- 第二节 科学探究:液体的压强
- 第三节 空气的“力量”
- 第四节 流体压强与流速的关系
- 第九章 浮力
- 第一节 认识浮力
- 第二节 阿基米德原理
- 第三节 物体的浮与沉
- 第十章 机械与人
- 第一节 科学探究:杠杆的平衡条件
- 第二节 滑轮及其应用
- 第三节 做功了吗
- 第四节 做功的快慢
- 第五节 机械效率
- 第六节 合理利用机械能
- 第十一章 小粒子与大宇宙
- 第一节 走进微观
- 第二节 看不见的运动
- 第三节 探索宇宙
