苏教版数学必修2第1章 立体几何初步1.2 点、线、面之间的位置关系 1.2.3 直线与平面的位置关系(word版教案)
文档属性
| 名称 | 苏教版数学必修2第1章 立体几何初步1.2 点、线、面之间的位置关系 1.2.3 直线与平面的位置关系(word版教案) |

|
|
| 格式 | zip | ||
| 文件大小 | 227.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-11 07:49:49 | ||
图片预览


文档简介
第1章 立体几何初步 第十一课时
1.2.3 直线与平面的位置关系(3)
【教学目标】
1.理解垂线段,斜线段,射影的概念;
2.了解直线与平面所成的角;
3.进一步理解“线线垂直”“线面垂直”的等价转换思想。
【教学重点】
直线和平面垂直的判定定理和性质定理的综合应用。
【教学难点】
直线和平面垂直的判定定理和性质定理的应用时定理成立条件的构建。
【过程方法】
通过探究、思考,运用直线和平面垂直的判定定理和性质定理解决有关的问题,使学生进一步理解解决立体几何问题的基本指导思想,即创造条件将空间的问题转化为平面的问题来解决。
【教学过程】
一、复习引入
1.直线与平面的位置关系;
2.直线与平面平行的判定与性质;
3.直线与平面垂直的判定与性质;
4.观察长方体ABCD-A1B1C1D1,判断直线A1B,A1C,A1D与平面ABCD的位置关系。
二、讲授新课
1.斜线、斜足、斜线段
一条直线与一个平面相交,但不和这个平面垂直,这条直线叫做这个平面的斜线。斜线与这个平面的交点叫做斜足,斜线上一点与斜足间的线段叫做这个点到平面的斜线段。
2.射影
过平面外一点P向平面α引斜线和垂线,那么过斜足Q和垂足P1的直线就是斜线在这个平面内的正投影,简称射影。
3.直线与平面所成的角
平面的一条斜线与它在这个平面内的射影所成的锐角,叫做直线与这个平面所成的角。
规定:一条直线垂直于一个平面,则说它们所成的角为直角;一条直线与平面平行或在平面内,则说它们所成的角是的角。
三、例题选讲
例1.正方体ABCD-A1B1C1D1中,。.
(1)求A1B与平面AC所成的角;
(2)设BD与AC的交点为O,求D1O与平面ABCD所成的角。
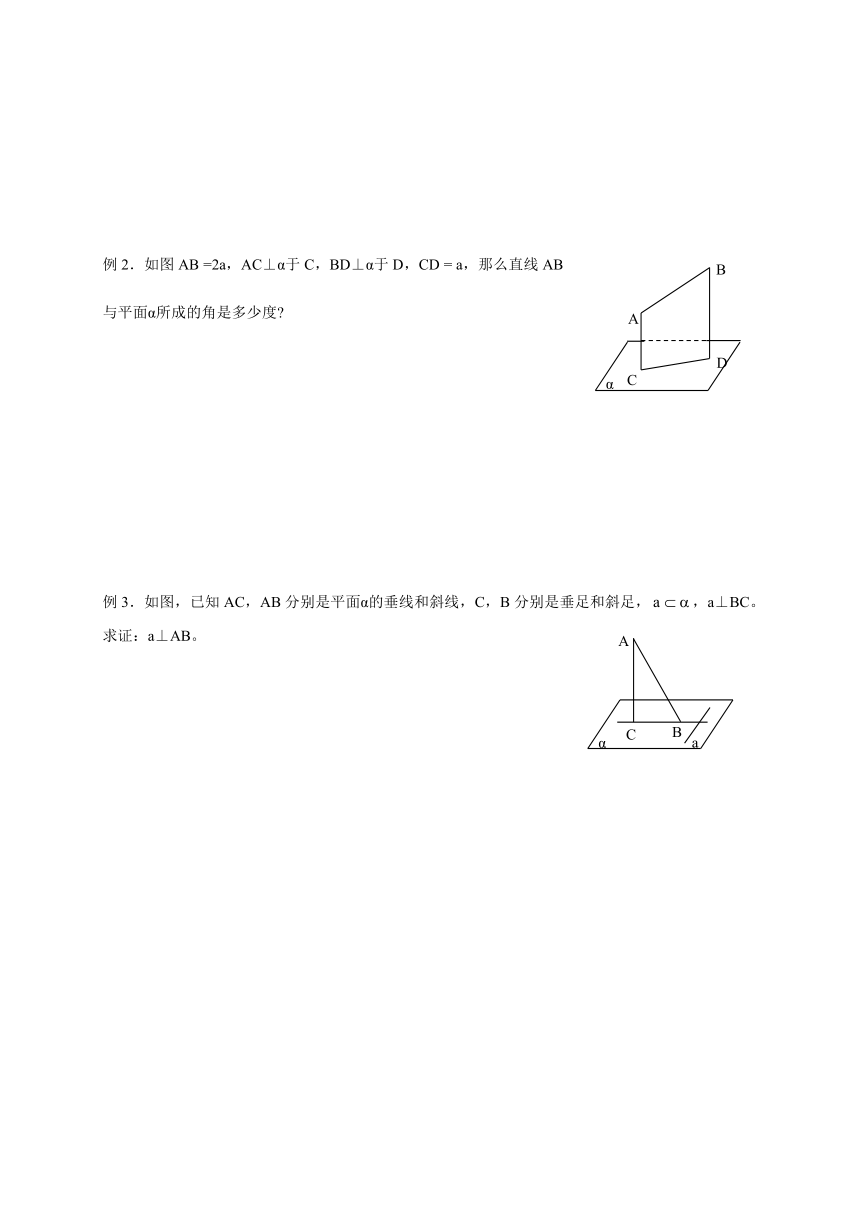
例2.如图AB =2a,AC⊥α于C,BD⊥α于D,CD = a,那么直线AB
与平面α所成的角是多少度?
例3.如图,已知AC,AB分别是平面α的垂线和斜线,C,B分别是垂足和斜足,,a⊥BC。求证:a⊥AB。
例4.如图,已知∠BAC在平面α内,,∠PAB=∠PAC。求证:点P在平面α上射影在∠BAC的平分线上。
四、课堂练习
1.课本书P37练习1、2、3、4;
2.正方体ABCD-A1B1C1D1中,对角线AC1与面对角线BD垂直,你能说出这个结论的理由吗?
3.已知点O是△ABC三条高的交点,PO⊥面ABC,连A、O并延长AO与BC相交,试说明PA⊥BC。
4.点P在△ABC内的射影为O,且PA、PB、PC两两垂直,求证O是△ABC的垂心。
【布置作业】
1. 在长方体中,线段中,长度等于D到平面距离的是 。
2. 平面的斜线与所成的角是,则它和内所有不过斜足的直线所成的角中,最大的角为 。
3. 设直线与平面所成的角为,则的范围是 。
4. 如图(1),所在的平面,则当 时,;当 时,。
5. 如图(2),在正方体中,E为的中点。(1)画出在平面上的射影 ;(2)画出在平面上的射影 ;(3)画出E点在平面上的射影 。
6. 若平面外的一条直线上的两点到这个平面的距离相等,则这条直线和平面的位置关系
为 。
7. 已知A,B两点到平面的距离分别为,AB与所成的角为,则线段AB在上的射影长为 。
8. (1)两条异面直线在同一平面上的射影可能有 种情况,
分别是 ;
(2)两条相交直线在同一平面上的射影可能有 种情况,
分别是 。
9. 是直线,是平面,下列判断正确的是 。
(1)平行于内无数条直线,则;
(2)则;
(3)则;
(4)若则。
10. 下列结论中,不正确的是 。
(1) (2)
(3) (4)与不垂直与可能平行。
11. 如图,已知:于A,EB于B,。求证:
A
B
C
D
A1
B1
D1
C1
P1
Q
α
P
B
A
C
D
A1
B1
D1
C1
O
C
D
α
A
B
C
B
a
α
A
F
E
A
B
P
O
C
O
P
C
A
B
B
A
C
D
A1
B1
D1
C1
O
O
P
C
A
B
D
A
B
C
D
P
(1)
E
(2)
A
B
C
D
A
B
E
