1.4 解直角三角形 同步练习(解析版)
文档属性
| 名称 | 1.4 解直角三角形 同步练习(解析版) | 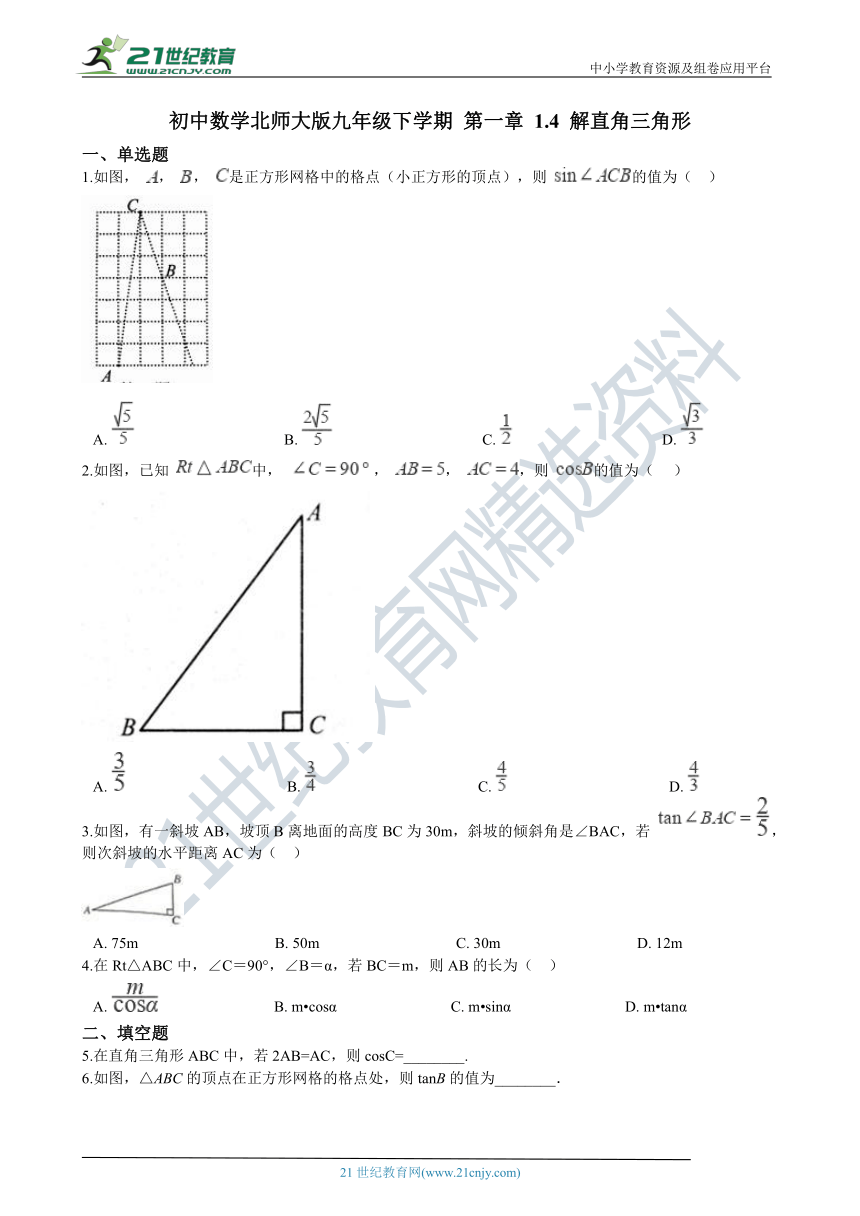 | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-06 16:14:40 | ||
图片预览



文档简介
初中数学北师大版九年级下学期 第一章 1.4 解直角三角形
一、单选题
1.如图, , , 是正方形网格中的格点(小正方形的顶点),则 的值为(?? )
A.????????????????????????????????????????B.????????????????????????????????????????C.????????????????????????????????????????D.?
2.如图,已知 中, , , ,则 的值为(??? )
A.???????????????????????????????????????????B.???????????????????????????????????????????C.???????????????????????????????????????????D.?
3.如图,有一斜坡AB,坡顶B离地面的高度BC为30m,斜坡的倾斜角是∠BAC,若 ,则次斜坡的水平距离AC为(?? ) 21cnjy.com21世纪教育网版权所有
A.?75m????????????????????????????????????B.?50m????????????????????????????????????C.?30m????????????????????????????????????D.?12m
4.在Rt△ABC中,∠C=90°,∠B=α,若BC=m,则AB的长为(?? )
A.???????????????????????????????B.?m?cosα??????????????????????????????C.?m?sinα??????????????????????????????D.?m?tanα
二、填空题
5.在直角三角形ABC中,若2AB=AC,则cosC=________.
6.如图,△ABC的顶点在正方形网格的格点处,则tanB的值为________.
7.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左侧墙上与地面成60°角时,梯子顶端距离地面2 米,若保持梯子底端位置不动,将梯子斜靠在右端时,与地面成45°,则小巷的宽度为________米(结果保留根号). 21·世纪*教育网21教育网
8.在Rt△ABC中, ,则cosB的值等于________.
9.在△ABC中,∠A,∠B都是锐角,且sinA= ,tanB= ,AB=10,则△ABC的面积为________.
10.Rt△ABC中,∠B=90°,AB=9,BC=12,则斜边上的高为________.
11.如图,在 中, , , ,点 是 的重心,连接 并延长交 于点 ,则 ________. www-2-1-cnjy-com21cnjy.com
三、综合题
12.如图,△ABC中,∠B=45°,AB=3 ,D是BC中点,tanC= .
求:
(1)BC的长;
(2)sin∠ADB.
答案解析部分
一、单选题
1.A
解:设小正方形的边长为1,过点B作BD⊥AC于D,过点B作BF⊥AE于点F,
∵S△ABC=2×7- ×1×3? ×1×7? ×2×4=5,
由勾股定理可知:AC= ,
∵ AC?BD=5,
∴BD= ,
由勾股定理可知:BC= ,
∴sin∠ACB= = .
故答案为:A.
【分析】设小正方形的边长为1,过点B作BD⊥AC于D,过点B作BF⊥AE于点F,根据网格图的特征可求出S?ABC的值,用勾股定理可求得AC和BC的长,然后在直角三角形BCD中,根据sin∠ACB=可求解。21世纪21世纪教育网有21·cn·jy·com
2.A
∵Rt△ABC中,∠C=90°,AB=5,AC=4,
∴BC= =3,
∴cosB= .
故答案为:A.
【分析】本题首先用勾股定理求出BC的长度,再用三角函数求出∠B的余弦值即可。
3.A
解:因为 ,又BC=30,所以, ,解得:AC=75m,
故答案为:A.
【分析】利用三角函数解直角三角形,可得到AC的距离。
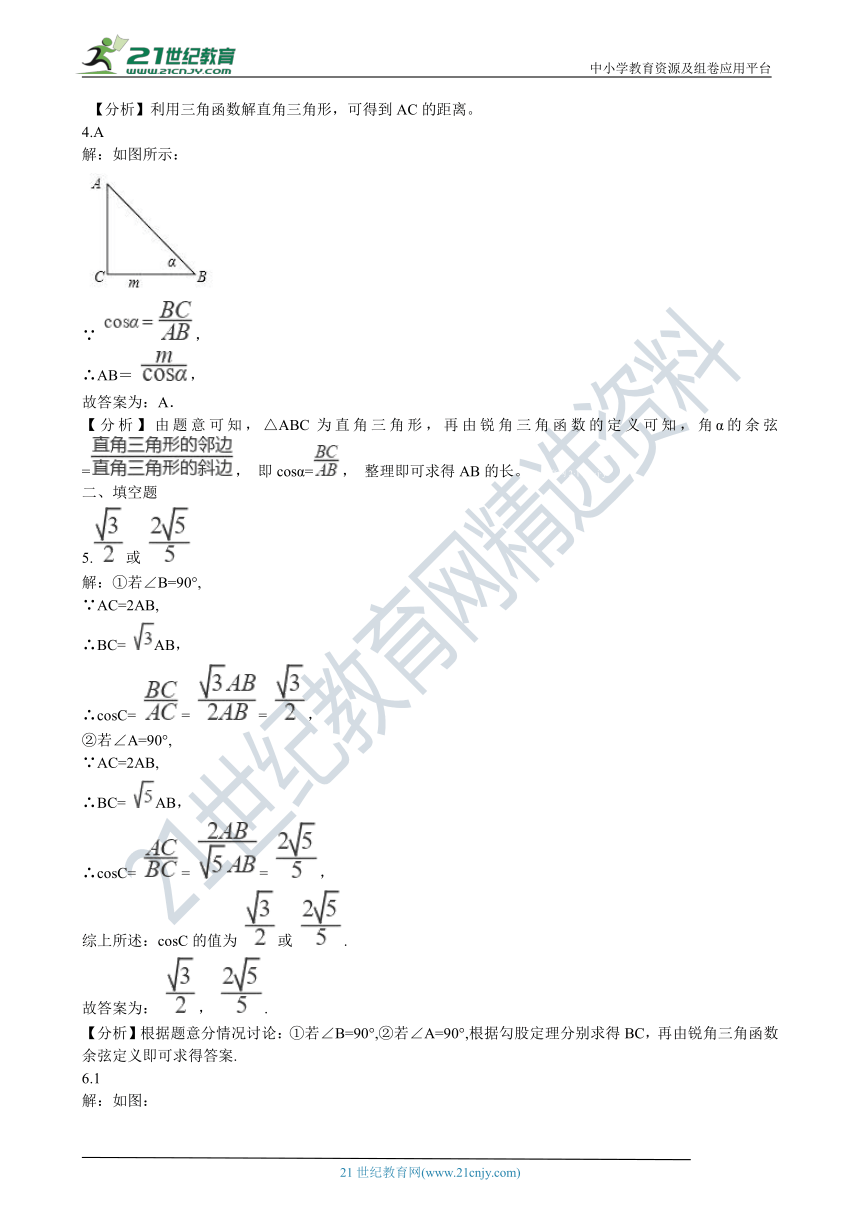
4.A
解:如图所示:
∵ ,
∴AB= ,
故答案为:A.
【分析】由题意可知,△ABC为直角三角形,再由锐角三角函数的定义可知,角α的余弦=, 即cosα=, 整理即可求得AB的长。21教育网2·1·c·n·j·y
二、填空题
5.或
解:①若∠B=90°,
∵AC=2AB,
∴BC= AB,
∴cosC= = = ,
②若∠A=90°,
∵AC=2AB,
∴BC= AB,
∴cosC= = = ,
综上所述:cosC的值为 或 .
故答案为: , .
【分析】根据题意分情况讨论:①若∠B=90°,②若∠A=90°,根据勾股定理分别求得BC,再由锐角三角函数余弦定义即可求得答案.21世纪教育网21-cn-jy.com【来源:21·世纪·教育·网】
6.1
解:如图:
由正切函数的定义,得tanB= ,
故答案为:1.
【分析】本题需要利用网格构造直角三角形,再利用三角函数就可以解决,
7.
解:如图所示:
AB=2 米,∠ACB=60°,∠DCE=45°,AC=CE.
则在直角三角形ABC中,
=tan∠ACB=tan60°= ,
=sin∠ACB=sin60°= ,
∴BC= = =2,AC= = =4,
∴直角三角形DCE中,CE=AC=4,
∴ =cos45°= ,
∴CD=CE× =4× =2 ,
∴BD=2+2 ,
故答案为:2+2 .
【分析】AB=2 米,∠ACB=60°,∠DCE=45°,AC=CE,利用解直角三角形分别求出BC,AC的长;再在Rt△DCE中,利用解直角三角形求出CD,然后求出BD的长。21·cn·jy·com21·世纪*教育网
8.
解:∵∠C=90°,
∴∠A+∠B=90°,
∴cosB=sinA,
∵sinA= ,
∴cosB= .
故答案为: .
【分析】 在直角三角形中,由锐角三角函数关系可得cosB=sinA= 可求解。
9.
解:∵在△ABC中,∠A、∠B都是锐角,sinA= ,tanB= ,
∴∠A=30°,∠B=60°,∠C=90°,
∵sinA= = ,tanB= = ,AB=10,
∴a= c=5,b= a=5 ,
∴S△ABC= ab= ×5×5 = ,
故答案为: .
【分析】通过sinA和tanB的值推出∠A和∠B的值,由此得出△ABC为直角三角形,那么已知AB=10,即可通过三角函数的定义计算出Rt△ABC中BC与AC的长度,从而计算出面积。
10.
Rt△ABC中,∠B=90°,AB=9,BC=12,所以斜边AC=15,
SRt△ABC= AB·BC=54
所以斜边上的高为
故填
【分析】根据三角形的面积表达方法,可解出斜边上的高。
11.
解:在Rt△ACB中,sinB= = ,AC=3,
∴AB=4,
∵点G是△ABC的重心,
∴点M是AB的中点,
在Rt△ACB中,点M是AB的中点,
∴CM= AB=2,
∵点M是AB的中点,
∴CG= CM= .
故答案为: . 【分析】根据sinB==可求得AB的值,由三角形重心的性质可得点M是AB的中点,由直角三角形斜边上的中线等于斜边的一半可得CM=AB,则CG=CM可求解。【来源:21·世纪·教育·网】
三、综合题
12.(1)解:过A作AE BC,AB=3 ,
勾股定理知,
所以AE=BE=3,
因为tanC= ,
所以EC=15,所以BC=18
(2)解:D是中点,所以BD=9,DE=6,AD= 所以sin∠ADB= .
【分析】(1) 过A作AE⊥BC,由题意易得AE=BE,根据tanC=可求得EC的值,则BC=BE+CE可求解; (2)由线段中点的定义可得BD=CD,则DE=BD-BE,用勾股定理可求得AD的值,再根据sin∠ADB=可求解。??2·1·c·n·j·ywww.21-cn-jy.com
一、单选题
1.如图, , , 是正方形网格中的格点(小正方形的顶点),则 的值为(?? )
A.????????????????????????????????????????B.????????????????????????????????????????C.????????????????????????????????????????D.?
2.如图,已知 中, , , ,则 的值为(??? )
A.???????????????????????????????????????????B.???????????????????????????????????????????C.???????????????????????????????????????????D.?
3.如图,有一斜坡AB,坡顶B离地面的高度BC为30m,斜坡的倾斜角是∠BAC,若 ,则次斜坡的水平距离AC为(?? ) 21cnjy.com21世纪教育网版权所有
A.?75m????????????????????????????????????B.?50m????????????????????????????????????C.?30m????????????????????????????????????D.?12m
4.在Rt△ABC中,∠C=90°,∠B=α,若BC=m,则AB的长为(?? )
A.???????????????????????????????B.?m?cosα??????????????????????????????C.?m?sinα??????????????????????????????D.?m?tanα
二、填空题
5.在直角三角形ABC中,若2AB=AC,则cosC=________.
6.如图,△ABC的顶点在正方形网格的格点处,则tanB的值为________.
7.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左侧墙上与地面成60°角时,梯子顶端距离地面2 米,若保持梯子底端位置不动,将梯子斜靠在右端时,与地面成45°,则小巷的宽度为________米(结果保留根号). 21·世纪*教育网21教育网
8.在Rt△ABC中, ,则cosB的值等于________.
9.在△ABC中,∠A,∠B都是锐角,且sinA= ,tanB= ,AB=10,则△ABC的面积为________.
10.Rt△ABC中,∠B=90°,AB=9,BC=12,则斜边上的高为________.
11.如图,在 中, , , ,点 是 的重心,连接 并延长交 于点 ,则 ________. www-2-1-cnjy-com21cnjy.com
三、综合题
12.如图,△ABC中,∠B=45°,AB=3 ,D是BC中点,tanC= .
求:
(1)BC的长;
(2)sin∠ADB.
答案解析部分
一、单选题
1.A
解:设小正方形的边长为1,过点B作BD⊥AC于D,过点B作BF⊥AE于点F,
∵S△ABC=2×7- ×1×3? ×1×7? ×2×4=5,
由勾股定理可知:AC= ,
∵ AC?BD=5,
∴BD= ,
由勾股定理可知:BC= ,
∴sin∠ACB= = .
故答案为:A.
【分析】设小正方形的边长为1,过点B作BD⊥AC于D,过点B作BF⊥AE于点F,根据网格图的特征可求出S?ABC的值,用勾股定理可求得AC和BC的长,然后在直角三角形BCD中,根据sin∠ACB=可求解。21世纪21世纪教育网有21·cn·jy·com
2.A
∵Rt△ABC中,∠C=90°,AB=5,AC=4,
∴BC= =3,
∴cosB= .
故答案为:A.
【分析】本题首先用勾股定理求出BC的长度,再用三角函数求出∠B的余弦值即可。
3.A
解:因为 ,又BC=30,所以, ,解得:AC=75m,
故答案为:A.
【分析】利用三角函数解直角三角形,可得到AC的距离。
4.A
解:如图所示:
∵ ,
∴AB= ,
故答案为:A.
【分析】由题意可知,△ABC为直角三角形,再由锐角三角函数的定义可知,角α的余弦=, 即cosα=, 整理即可求得AB的长。21教育网2·1·c·n·j·y
二、填空题
5.或
解:①若∠B=90°,
∵AC=2AB,
∴BC= AB,
∴cosC= = = ,
②若∠A=90°,
∵AC=2AB,
∴BC= AB,
∴cosC= = = ,
综上所述:cosC的值为 或 .
故答案为: , .
【分析】根据题意分情况讨论:①若∠B=90°,②若∠A=90°,根据勾股定理分别求得BC,再由锐角三角函数余弦定义即可求得答案.21世纪教育网21-cn-jy.com【来源:21·世纪·教育·网】
6.1
解:如图:
由正切函数的定义,得tanB= ,
故答案为:1.
【分析】本题需要利用网格构造直角三角形,再利用三角函数就可以解决,
7.
解:如图所示:
AB=2 米,∠ACB=60°,∠DCE=45°,AC=CE.
则在直角三角形ABC中,
=tan∠ACB=tan60°= ,
=sin∠ACB=sin60°= ,
∴BC= = =2,AC= = =4,
∴直角三角形DCE中,CE=AC=4,
∴ =cos45°= ,
∴CD=CE× =4× =2 ,
∴BD=2+2 ,
故答案为:2+2 .
【分析】AB=2 米,∠ACB=60°,∠DCE=45°,AC=CE,利用解直角三角形分别求出BC,AC的长;再在Rt△DCE中,利用解直角三角形求出CD,然后求出BD的长。21·cn·jy·com21·世纪*教育网
8.
解:∵∠C=90°,
∴∠A+∠B=90°,
∴cosB=sinA,
∵sinA= ,
∴cosB= .
故答案为: .
【分析】 在直角三角形中,由锐角三角函数关系可得cosB=sinA= 可求解。
9.
解:∵在△ABC中,∠A、∠B都是锐角,sinA= ,tanB= ,
∴∠A=30°,∠B=60°,∠C=90°,
∵sinA= = ,tanB= = ,AB=10,
∴a= c=5,b= a=5 ,
∴S△ABC= ab= ×5×5 = ,
故答案为: .
【分析】通过sinA和tanB的值推出∠A和∠B的值,由此得出△ABC为直角三角形,那么已知AB=10,即可通过三角函数的定义计算出Rt△ABC中BC与AC的长度,从而计算出面积。
10.
Rt△ABC中,∠B=90°,AB=9,BC=12,所以斜边AC=15,
SRt△ABC= AB·BC=54
所以斜边上的高为
故填
【分析】根据三角形的面积表达方法,可解出斜边上的高。
11.
解:在Rt△ACB中,sinB= = ,AC=3,
∴AB=4,
∵点G是△ABC的重心,
∴点M是AB的中点,
在Rt△ACB中,点M是AB的中点,
∴CM= AB=2,
∵点M是AB的中点,
∴CG= CM= .
故答案为: . 【分析】根据sinB==可求得AB的值,由三角形重心的性质可得点M是AB的中点,由直角三角形斜边上的中线等于斜边的一半可得CM=AB,则CG=CM可求解。【来源:21·世纪·教育·网】
三、综合题
12.(1)解:过A作AE BC,AB=3 ,
勾股定理知,
所以AE=BE=3,
因为tanC= ,
所以EC=15,所以BC=18
(2)解:D是中点,所以BD=9,DE=6,AD= 所以sin∠ADB= .
【分析】(1) 过A作AE⊥BC,由题意易得AE=BE,根据tanC=可求得EC的值,则BC=BE+CE可求解; (2)由线段中点的定义可得BD=CD,则DE=BD-BE,用勾股定理可求得AD的值,再根据sin∠ADB=可求解。??2·1·c·n·j·ywww.21-cn-jy.com
