1.5 三角函数的应用 同步练习(解析版)
文档属性
| 名称 | 1.5 三角函数的应用 同步练习(解析版) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-06 00:00:00 | ||
图片预览




文档简介
初中数学北师大版九年级下学期 第一章 1.5 三角函数的应用
一、单选题
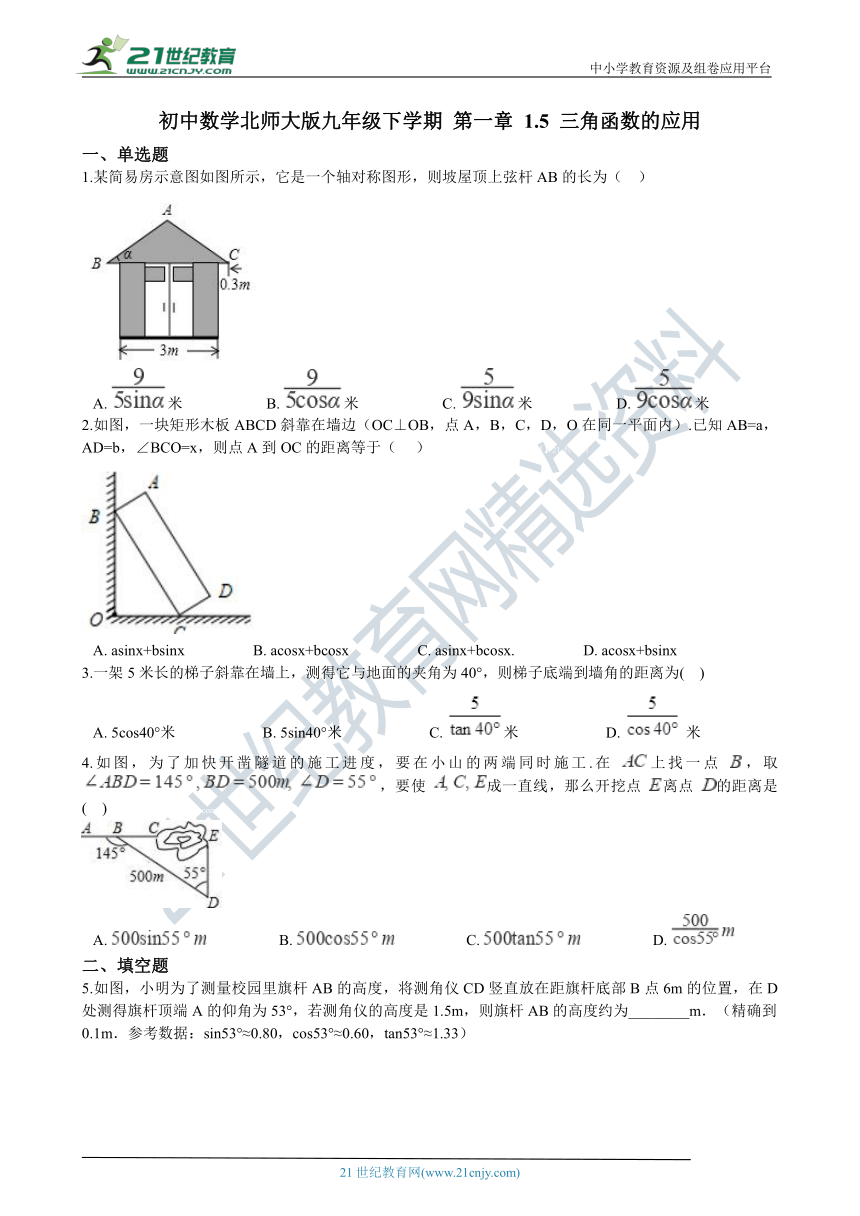
1.某简易房示意图如图所示,它是一个轴对称图形,则坡屋顶上弦杆AB的长为( ??)
A.?米??????????????????????B.?米??????????????????????C.?米??????????????????????D.?米
2.如图,一块矩形木板ABCD斜靠在墙边(OC⊥OB,点A,B,C,D,O在同一平面内).已知AB=a,AD=b,∠BCO=x,则点A到OC的距离等于(??? )【来源:21·世纪·教育·网】21教育网
A.?asinx+bsinx??????????????????B.?acosx+bcosx??????????????????C.?asinx+bcosx.??????????????????D.?acosx+bsinx
3.一架5米长的梯子斜靠在墙上,测得它与地面的夹角为40°,则梯子底端到墙角的距离为(?? )
A.?5cos40°米???????????????????????B.?5sin40°米???????????????????????C.?米???????????????????????D.??米
4.如图,为了加快开凿隧道的施工进度,要在小山的两端同时施工.在 上找一点 ,取 ,要使 成一直线,那么开挖点 离点 的距离是(?? ) 21*cnjy*com21·cn·jy·com
A.????????????????????B.????????????????????C.????????????????????D.?
二、填空题
5.如图,小明为了测量校园里旗杆AB的高度,将测角仪CD竖直放在距旗杆底部B点6m的位置,在D处测得旗杆顶端A的仰角为53°,若测角仪的高度是1.5m,则旗杆AB的高度约为________m.(精确到0.1m.参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33) 【来源:21cnj*y.co*m】www.21-cn-jy.com
三、解答题
6.如图,池塘边一棵垂直于水面BM的笔直大树AB在点C处折断,AC部分倒下,点A与水面上的点E重合,部分沉入水中后,点A与水中的点F重合,CF交水面于点D,DF=2m,∠CEB=30°,∠CDB=45°,求CB部分的高度.(精确到0.1m.参考数据: ≈1.41, ≈1.73) 21*cnjy*com2·1·c·n·j·y
7.为了保证人们上下楼的安全,楼梯踏步的宽度和高度都要加以限制.中小学楼梯宽度的范围是260mm~300mm含(300mm),高度的范围是120mm~150mm(含150mm).如图是某中学的楼梯扶手的截面示意图,测量结果如下:AB,CD分别垂直平分踏步EF,GH,各踏步互相平行,AB=CD,AC=900mm,∠ACD=65°,试问该中学楼梯踏步的宽度和高度是否符合规定.(结果精确到1mm,参考数据:sin65°≈0.906,cos65°≈0.423) 21·cn·jy·com21·世纪*教育网
8.图1是一辆在平地上滑行的滑板车,图2是其示意图,已知车杆AB长92cm,车杆与脚踏板所成的角∠ABC=70°,前后轮子的半径均为6cm,求把手A离地面的高度(结果保留小数点后一位:参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)21教育网www-2-1-cnjy-com
9.如图所示,A、B、C为三个村庄,AB、BC、AD为公路,CD为河宽,现在要从D处开始铺设通往村庄C的一条地下电缆,A、C、D三点共线,经测量得,BC=6 千米,AD=4千米,∠A=60°,∠BCA=45°,请求出河宽CD的长(结果保留根号)。 21*cnjy*com
10.如图,从A地到B地的公路需要经过C地,图中AC=10千米,∠CAB=25°,∠CBA=37°。因城市规划的需要,将在A,B两地之间修建一条笔直的公路。 【来源:21cnj*y.co*m】
(1)求改直后的公路AB的长;
(2)问:公路改造后比原来缩短了多少千米?
(sin25°≈0.42,cos25°≈0.91,sin37°≈0.60,tan37°≈0.75)
答案解析部分
一、单选题
1. B
解:∵简易房为轴对称图像,故BC边上的高平分底边,
∴有 ?故答案为:B。
【分析】由轴对称关系,作高,解直角三角形即可。
2. D
解:作AG⊥OC交OC于点G,交BC于点H,如图,
∵四边形ABCD为矩形,AD=b,
∴∠ABH=90°,AD=BC=b,
∵OB⊥OC,
∴∠O=90°,
又∵∠HCG+∠GHC=90°,∠AHB+∠BAH=90°,∠GHC=∠AHB,∠BC0=x,
∴∠HCG=∠BAH=x,
在Rt△ABH中,
∵cos∠BAH=cosx= ,AB=a,
∴AH= ,
∵tan∠BAH=tanx= ,
∴BH=a·tanx,
∴CH=BC-BH=b-a·tanx,
在Rt△CGH中,
∵sin∠HCG=sinx= ,
∴GH=(b-a·tanx)·sinx=bsinx-atanxsinx,
∴AG=AH+HG= +bsinx-atanxsinx,
= +bsinx- ,
=bsinx+acosx.
故答案为:D.
【分析】作AG⊥OC交OC于点G,交BC于点H,由矩形性质得∠ABH=90°,AD=BC=b,根据等角的余角相等得∠HCG=∠BAH=x,在Rt△ABH中,根据锐角三角函数余弦定义cosx= 得AH= ,根据锐角三角函数正切定义tanx= 得BH=a·tanx,从而可得CH长,在Rt△CGH中,根据锐角三角函数正弦定义sinx= 得GH=bsinx-atanxsinx,由AG=AH+HG计算即可得出答案.
3. A
解:根据题意画出图形,如图, 在Rt△ACB中, ∵cosθ=, 即cos40°=, ∴AC=5cos40°. 故答案为:A. 【分析】根据题意画出图形,在Rt△ACB中,根据锐角三角函数余弦定义即可求得答案.
4. B
∵点A、C、E在同一直线上,∠ABD=145°,∠BDE=55°,
∴∠DEB=90°,
∴DE=BD×cos∠BDE.
∵BD=500米,∠BDE=55°,
∴DE=500cos55°米.
即开挖点E离点D的距离是500cos55°米.
故答案为:B.
【分析】当点A、C、E在同一直线上时,根据三角形外角定理得出∠DEB=90°,在Rt△BDE中,根据余弦函数的定义,由DE=BD×cos∠BDE即可得出答案。2-1-c-n-j-y2-1-c-n-j-y
二、填空题
5. 9.5
解:过D作DE⊥AB,
∵在D处测得旗杆顶端A的仰角为53°,
∴∠ADE=53°,
∵BC=DE=6m,
∴AE=DE?tan53°≈6×1.33≈7.98m,
∴AB=AE+BE=AE+CD=7.98+1.5=9.48m≈9.5m,
故答案为:9.5
【分析】过点D作DE⊥AB,解直角三角形求出AE的长即可解决问题.
三、解答题
6. 解:设CB部分的高度为xm.
∵∠BDC=∠BCD=45°,
∴BC=BD=xm.
在Rt△BCD中,CD= = = x(m).
在Rt△BCE中,∵∠BEC=30°,
∴CE=2BC=2x(m).
∵CE=CF=CD+DF,
∴2x= x+2,
解得:x=2+ .
∴BC=2+ ≈3.4(m).
答:CB部分的高度约为3.4m。
【分析】 设CB部分的高度为xm,根据等腰直角三角形的性质得出 BC=BD=xm,在 Rt△BCD中,根据正弦函数的定义及特殊锐角三角函数值,由CD= 表示出CD的长, 在Rt△BCE中 ,根据含30°直角三角形的边之间的关系得出 CE=2BC=2x(m),从而根据 CE=CF=CD+DF, 列出方程求解算出x的值,得出答案.21cnjy.com【来源:21·世纪·教育·网】
7. 解:连接BD,作DM⊥AB于点M,
∵AB=CD,AB,CD分别垂直平分踏步EF,GH,
∴AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,
∴∠C=∠ABD,AC=BD,
∵∠C=65°,AC=900,
∴∠ABD=65°,BD=900,
∴BM=BD?cos65°=900×0.423≈381,DM=BD?sin65°=900×0.906≈815,21世纪21世纪教育网有
∵381÷3=127,120<127<150,
∴该中学楼梯踏步的高度符合规定,
∵815÷3≈272,260<272<300,
∴该中学楼梯踏步的宽度符合规定,
由上可得,该中学楼梯踏步的宽度和高度都符合规定.
【分析】 连接BD,作DM⊥AB于点M, 首先判断出四边形ABCD是平行四边形, 根据平行四边形的性质得出 ∠C=∠ABD,AC=BD, 根据锐角三角函数的定义,由 BM=BD?cos65° 及 DM=BD?sin65° 即可求出BM,DM的长,进而即可判断 楼梯踏步的高度及宽度是否符合题意.
8. 解:将滑板车看作AB、BC两条直线,作AD垂直于BC,
A离地面高度即AD的长度加上轮胎半径,则Sin∠B=Sin∠70°= ≈0.94,所以AD≈86.5厘米,则A离地面高度为86.5+5=92.5厘米21·世纪*教育网21世纪教育网版权所有
【分析】作AD⊥BC,在Rt△ADB中,根据锐角三角函数正弦定义可求得AD长,由AD+轮胎半径即为把手A离地面的高度.www-2-1-cnjy-com【出处:21教育名师】
9. 解:过点B作BE⊥AC,垂足为E,
∵BC=6 ,∠BCA=45°
∴BE=EC=6
又∠A=60°
∴tan60°=
∴AE=2
∴AC=2 +6
又AD=4
∴CD=AC-AD=2 +6-4=2 +2(千米)
答:河宽CD的长是(2 +2)千米。
【分析】过点B作BE⊥AC,垂足为E,根据等腰直角三角形的性质得出BE=EC=6,根据正切函数的定义及特殊锐角三角函数值,由tan60°= 即可算出AE的长,进而根据线段的和差即可算出CD的长。21世纪教育网21-cn-jy.com21cnjy.com
10. (1)解:作CH⊥AB于H. 在Rt△ACH中,CH=AC?sin∠CAB=AC?sin25°≈10×0.42=4.2(千米), 【出处:21教育名师】【版权所有:21教育】
AH=AC?cos∠CAB=AC?cos25°≈10×0.91=9.1(千米),
在Rt△BCH中,BH=CH÷tan∠CBA=4.2÷tan37°≈4.2÷0.75=5.6(千米),【版权所有:21教育】
∴AB=AH+BH=9.1+5.6=14.7(千米).?? 故改直的公路AB的长14.7千米
(2)解:在Rt△BCH中,BC=CH÷sin∠CBA=4.2÷sin37°≈4.2÷0.6=7(千米), 2·1·c·n·j·y
则AC+BC﹣AB=10+7﹣14.7=2.3(千米). 答:公路改直后比原来缩短了2.3千米
【分析】(1) 作CH⊥AB于H. 在Rt△ACH中,根据正弦函数的定义,由CH=AC?sin∠CAB 算出CH的长,根据余弦函数的定义,由AH=AC?cos∠CAB 算出AH的长, 在Rt△BCH中,根据正切函数的定义,由BH=CH÷tan∠CBA 算出BH的长,最后根据AB=AH+BH即可算出答案; (2) 在Rt△BCH中,根据正弦函数的定义,由BC=CH÷sin∠CBA 算出BC的长,最后根据 AC+BC﹣AB 即可算出答案。21教育名师原创作品21教育名师原创作品
一、单选题
1.某简易房示意图如图所示,它是一个轴对称图形,则坡屋顶上弦杆AB的长为( ??)
A.?米??????????????????????B.?米??????????????????????C.?米??????????????????????D.?米
2.如图,一块矩形木板ABCD斜靠在墙边(OC⊥OB,点A,B,C,D,O在同一平面内).已知AB=a,AD=b,∠BCO=x,则点A到OC的距离等于(??? )【来源:21·世纪·教育·网】21教育网
A.?asinx+bsinx??????????????????B.?acosx+bcosx??????????????????C.?asinx+bcosx.??????????????????D.?acosx+bsinx
3.一架5米长的梯子斜靠在墙上,测得它与地面的夹角为40°,则梯子底端到墙角的距离为(?? )
A.?5cos40°米???????????????????????B.?5sin40°米???????????????????????C.?米???????????????????????D.??米
4.如图,为了加快开凿隧道的施工进度,要在小山的两端同时施工.在 上找一点 ,取 ,要使 成一直线,那么开挖点 离点 的距离是(?? ) 21*cnjy*com21·cn·jy·com
A.????????????????????B.????????????????????C.????????????????????D.?
二、填空题
5.如图,小明为了测量校园里旗杆AB的高度,将测角仪CD竖直放在距旗杆底部B点6m的位置,在D处测得旗杆顶端A的仰角为53°,若测角仪的高度是1.5m,则旗杆AB的高度约为________m.(精确到0.1m.参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33) 【来源:21cnj*y.co*m】www.21-cn-jy.com
三、解答题
6.如图,池塘边一棵垂直于水面BM的笔直大树AB在点C处折断,AC部分倒下,点A与水面上的点E重合,部分沉入水中后,点A与水中的点F重合,CF交水面于点D,DF=2m,∠CEB=30°,∠CDB=45°,求CB部分的高度.(精确到0.1m.参考数据: ≈1.41, ≈1.73) 21*cnjy*com2·1·c·n·j·y
7.为了保证人们上下楼的安全,楼梯踏步的宽度和高度都要加以限制.中小学楼梯宽度的范围是260mm~300mm含(300mm),高度的范围是120mm~150mm(含150mm).如图是某中学的楼梯扶手的截面示意图,测量结果如下:AB,CD分别垂直平分踏步EF,GH,各踏步互相平行,AB=CD,AC=900mm,∠ACD=65°,试问该中学楼梯踏步的宽度和高度是否符合规定.(结果精确到1mm,参考数据:sin65°≈0.906,cos65°≈0.423) 21·cn·jy·com21·世纪*教育网
8.图1是一辆在平地上滑行的滑板车,图2是其示意图,已知车杆AB长92cm,车杆与脚踏板所成的角∠ABC=70°,前后轮子的半径均为6cm,求把手A离地面的高度(结果保留小数点后一位:参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)21教育网www-2-1-cnjy-com
9.如图所示,A、B、C为三个村庄,AB、BC、AD为公路,CD为河宽,现在要从D处开始铺设通往村庄C的一条地下电缆,A、C、D三点共线,经测量得,BC=6 千米,AD=4千米,∠A=60°,∠BCA=45°,请求出河宽CD的长(结果保留根号)。 21*cnjy*com
10.如图,从A地到B地的公路需要经过C地,图中AC=10千米,∠CAB=25°,∠CBA=37°。因城市规划的需要,将在A,B两地之间修建一条笔直的公路。 【来源:21cnj*y.co*m】
(1)求改直后的公路AB的长;
(2)问:公路改造后比原来缩短了多少千米?
(sin25°≈0.42,cos25°≈0.91,sin37°≈0.60,tan37°≈0.75)
答案解析部分
一、单选题
1. B
解:∵简易房为轴对称图像,故BC边上的高平分底边,
∴有 ?故答案为:B。
【分析】由轴对称关系,作高,解直角三角形即可。
2. D
解:作AG⊥OC交OC于点G,交BC于点H,如图,
∵四边形ABCD为矩形,AD=b,
∴∠ABH=90°,AD=BC=b,
∵OB⊥OC,
∴∠O=90°,
又∵∠HCG+∠GHC=90°,∠AHB+∠BAH=90°,∠GHC=∠AHB,∠BC0=x,
∴∠HCG=∠BAH=x,
在Rt△ABH中,
∵cos∠BAH=cosx= ,AB=a,
∴AH= ,
∵tan∠BAH=tanx= ,
∴BH=a·tanx,
∴CH=BC-BH=b-a·tanx,
在Rt△CGH中,
∵sin∠HCG=sinx= ,
∴GH=(b-a·tanx)·sinx=bsinx-atanxsinx,
∴AG=AH+HG= +bsinx-atanxsinx,
= +bsinx- ,
=bsinx+acosx.
故答案为:D.
【分析】作AG⊥OC交OC于点G,交BC于点H,由矩形性质得∠ABH=90°,AD=BC=b,根据等角的余角相等得∠HCG=∠BAH=x,在Rt△ABH中,根据锐角三角函数余弦定义cosx= 得AH= ,根据锐角三角函数正切定义tanx= 得BH=a·tanx,从而可得CH长,在Rt△CGH中,根据锐角三角函数正弦定义sinx= 得GH=bsinx-atanxsinx,由AG=AH+HG计算即可得出答案.
3. A
解:根据题意画出图形,如图, 在Rt△ACB中, ∵cosθ=, 即cos40°=, ∴AC=5cos40°. 故答案为:A. 【分析】根据题意画出图形,在Rt△ACB中,根据锐角三角函数余弦定义即可求得答案.
4. B
∵点A、C、E在同一直线上,∠ABD=145°,∠BDE=55°,
∴∠DEB=90°,
∴DE=BD×cos∠BDE.
∵BD=500米,∠BDE=55°,
∴DE=500cos55°米.
即开挖点E离点D的距离是500cos55°米.
故答案为:B.
【分析】当点A、C、E在同一直线上时,根据三角形外角定理得出∠DEB=90°,在Rt△BDE中,根据余弦函数的定义,由DE=BD×cos∠BDE即可得出答案。2-1-c-n-j-y2-1-c-n-j-y
二、填空题
5. 9.5
解:过D作DE⊥AB,
∵在D处测得旗杆顶端A的仰角为53°,
∴∠ADE=53°,
∵BC=DE=6m,
∴AE=DE?tan53°≈6×1.33≈7.98m,
∴AB=AE+BE=AE+CD=7.98+1.5=9.48m≈9.5m,
故答案为:9.5
【分析】过点D作DE⊥AB,解直角三角形求出AE的长即可解决问题.
三、解答题
6. 解:设CB部分的高度为xm.
∵∠BDC=∠BCD=45°,
∴BC=BD=xm.
在Rt△BCD中,CD= = = x(m).
在Rt△BCE中,∵∠BEC=30°,
∴CE=2BC=2x(m).
∵CE=CF=CD+DF,
∴2x= x+2,
解得:x=2+ .
∴BC=2+ ≈3.4(m).
答:CB部分的高度约为3.4m。
【分析】 设CB部分的高度为xm,根据等腰直角三角形的性质得出 BC=BD=xm,在 Rt△BCD中,根据正弦函数的定义及特殊锐角三角函数值,由CD= 表示出CD的长, 在Rt△BCE中 ,根据含30°直角三角形的边之间的关系得出 CE=2BC=2x(m),从而根据 CE=CF=CD+DF, 列出方程求解算出x的值,得出答案.21cnjy.com【来源:21·世纪·教育·网】
7. 解:连接BD,作DM⊥AB于点M,
∵AB=CD,AB,CD分别垂直平分踏步EF,GH,
∴AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,
∴∠C=∠ABD,AC=BD,
∵∠C=65°,AC=900,
∴∠ABD=65°,BD=900,
∴BM=BD?cos65°=900×0.423≈381,DM=BD?sin65°=900×0.906≈815,21世纪21世纪教育网有
∵381÷3=127,120<127<150,
∴该中学楼梯踏步的高度符合规定,
∵815÷3≈272,260<272<300,
∴该中学楼梯踏步的宽度符合规定,
由上可得,该中学楼梯踏步的宽度和高度都符合规定.
【分析】 连接BD,作DM⊥AB于点M, 首先判断出四边形ABCD是平行四边形, 根据平行四边形的性质得出 ∠C=∠ABD,AC=BD, 根据锐角三角函数的定义,由 BM=BD?cos65° 及 DM=BD?sin65° 即可求出BM,DM的长,进而即可判断 楼梯踏步的高度及宽度是否符合题意.
8. 解:将滑板车看作AB、BC两条直线,作AD垂直于BC,
A离地面高度即AD的长度加上轮胎半径,则Sin∠B=Sin∠70°= ≈0.94,所以AD≈86.5厘米,则A离地面高度为86.5+5=92.5厘米21·世纪*教育网21世纪教育网版权所有
【分析】作AD⊥BC,在Rt△ADB中,根据锐角三角函数正弦定义可求得AD长,由AD+轮胎半径即为把手A离地面的高度.www-2-1-cnjy-com【出处:21教育名师】
9. 解:过点B作BE⊥AC,垂足为E,
∵BC=6 ,∠BCA=45°
∴BE=EC=6
又∠A=60°
∴tan60°=
∴AE=2
∴AC=2 +6
又AD=4
∴CD=AC-AD=2 +6-4=2 +2(千米)
答:河宽CD的长是(2 +2)千米。
【分析】过点B作BE⊥AC,垂足为E,根据等腰直角三角形的性质得出BE=EC=6,根据正切函数的定义及特殊锐角三角函数值,由tan60°= 即可算出AE的长,进而根据线段的和差即可算出CD的长。21世纪教育网21-cn-jy.com21cnjy.com
10. (1)解:作CH⊥AB于H. 在Rt△ACH中,CH=AC?sin∠CAB=AC?sin25°≈10×0.42=4.2(千米), 【出处:21教育名师】【版权所有:21教育】
AH=AC?cos∠CAB=AC?cos25°≈10×0.91=9.1(千米),
在Rt△BCH中,BH=CH÷tan∠CBA=4.2÷tan37°≈4.2÷0.75=5.6(千米),【版权所有:21教育】
∴AB=AH+BH=9.1+5.6=14.7(千米).?? 故改直的公路AB的长14.7千米
(2)解:在Rt△BCH中,BC=CH÷sin∠CBA=4.2÷sin37°≈4.2÷0.6=7(千米), 2·1·c·n·j·y
则AC+BC﹣AB=10+7﹣14.7=2.3(千米). 答:公路改直后比原来缩短了2.3千米
【分析】(1) 作CH⊥AB于H. 在Rt△ACH中,根据正弦函数的定义,由CH=AC?sin∠CAB 算出CH的长,根据余弦函数的定义,由AH=AC?cos∠CAB 算出AH的长, 在Rt△BCH中,根据正切函数的定义,由BH=CH÷tan∠CBA 算出BH的长,最后根据AB=AH+BH即可算出答案; (2) 在Rt△BCH中,根据正弦函数的定义,由BC=CH÷sin∠CBA 算出BC的长,最后根据 AC+BC﹣AB 即可算出答案。21教育名师原创作品21教育名师原创作品
