沪教版数学七年级第一学期 9.15 十字相乘法 课件(16张PPT)
文档属性
| 名称 | 沪教版数学七年级第一学期 9.15 十字相乘法 课件(16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 215.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-08 16:00:44 | ||
图片预览



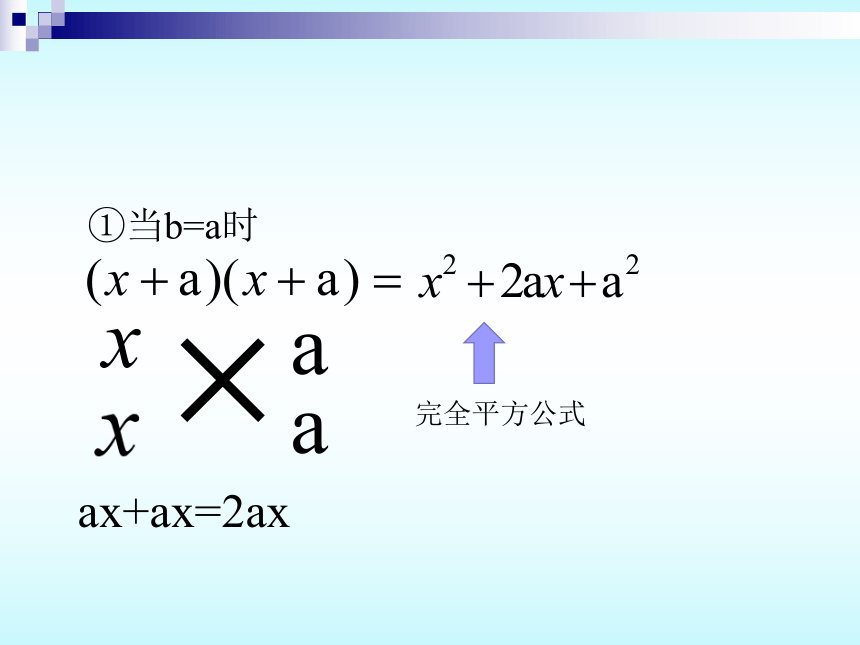



文档简介
(共16张PPT)
“十字相乘法”是乘法公式:(x+a)(x+b)=x2+(a+b)x+ab的逆运算。
十字相乘法
例、把 x2-x-6分解因式
例一:
步骤:
①分解二次项与常数项
②交叉相乘后的代数和为中间项
③检验中间项是否正确
十字相乘法(十字交叉分解因式)
(引出)
顺口溜:
前后因式分解交叉乘,
中间项为代数和。
一般形式:
①当b=a时
ax+ax=2ax
完全平方公式
②当b=-a时
ax+(-ax)=0
平方差公式
③首项有负号时(也是提取公因式时第一要点)
转化到我们熟悉分解方式
总结:
左边:不熟悉的
右边:熟悉的
完全平方公式
平方差公式
平方差公式
熟悉的例题
文字总结:提负号的目的不是为了提负号而提负号,而是为了回到我们熟悉的公式或者我们熟悉的例题(十字相乘法)中去下步因式分解。
题型④
题型⑤
题型④和⑤,我们一起与最开始引出十字相乘的例题x2-x-6一起对比来看,回到我们熟悉的例题里面
观察④最后一项-6多了一个因式y2,中间项多了一个因式 y
观察⑤最后一项-6多了一个因式
中间项多了一个因式
回到我们熟悉的分解方式
只需在右边分解的因式分别乘以多了的那个因式
题型④
另一个因式y
分别乘以
题型⑤
分别乘以
另一个因式(y2+1)
⑥
系数不为1
则需对前后两个因式的系数均分解,口算,心算能力不足时需要在草稿纸上写出多种十字交叉分解的情形,特别是当前后两项系数数值比较大。
⑦首项和末项为多个因式相乘,如abc
这种的分解方式比较多,难度较大,建议后期的学习中再慢慢了解
最后:关于十字相乘法的项数及次数问题,笔者认为,这个没有特定要求,如前面的例子平方差公式,只有两项也能用这种思想,再比如题型⑤
如果()里面是一个很项数的很多项式,同样看作一个整体,那也是可以用这种思想的,我认为类似于三个整式的代数和形式代数式均可考虑使用十字相乘法。
课堂练习
(1) x2-4x-21 (2) x2 + 4x - 21
(3) x2-5x-6 (4)x2-10x+21
(5)2x2 +3x+1 (6)2x2 - 3x+1
(7)2x2 +5x+2 (8)2x2 - 5x+2
(9)2x2-5xy+2y2
(12)(a+b)2 +5(a+b)-36
(11)
(10)6x2 -7xy-5y2
“十字相乘法”是乘法公式:(x+a)(x+b)=x2+(a+b)x+ab的逆运算。
十字相乘法
例、把 x2-x-6分解因式
例一:
步骤:
①分解二次项与常数项
②交叉相乘后的代数和为中间项
③检验中间项是否正确
十字相乘法(十字交叉分解因式)
(引出)
顺口溜:
前后因式分解交叉乘,
中间项为代数和。
一般形式:
①当b=a时
ax+ax=2ax
完全平方公式
②当b=-a时
ax+(-ax)=0
平方差公式
③首项有负号时(也是提取公因式时第一要点)
转化到我们熟悉分解方式
总结:
左边:不熟悉的
右边:熟悉的
完全平方公式
平方差公式
平方差公式
熟悉的例题
文字总结:提负号的目的不是为了提负号而提负号,而是为了回到我们熟悉的公式或者我们熟悉的例题(十字相乘法)中去下步因式分解。
题型④
题型⑤
题型④和⑤,我们一起与最开始引出十字相乘的例题x2-x-6一起对比来看,回到我们熟悉的例题里面
观察④最后一项-6多了一个因式y2,中间项多了一个因式 y
观察⑤最后一项-6多了一个因式
中间项多了一个因式
回到我们熟悉的分解方式
只需在右边分解的因式分别乘以多了的那个因式
题型④
另一个因式y
分别乘以
题型⑤
分别乘以
另一个因式(y2+1)
⑥
系数不为1
则需对前后两个因式的系数均分解,口算,心算能力不足时需要在草稿纸上写出多种十字交叉分解的情形,特别是当前后两项系数数值比较大。
⑦首项和末项为多个因式相乘,如abc
这种的分解方式比较多,难度较大,建议后期的学习中再慢慢了解
最后:关于十字相乘法的项数及次数问题,笔者认为,这个没有特定要求,如前面的例子平方差公式,只有两项也能用这种思想,再比如题型⑤
如果()里面是一个很项数的很多项式,同样看作一个整体,那也是可以用这种思想的,我认为类似于三个整式的代数和形式代数式均可考虑使用十字相乘法。
课堂练习
(1) x2-4x-21 (2) x2 + 4x - 21
(3) x2-5x-6 (4)x2-10x+21
(5)2x2 +3x+1 (6)2x2 - 3x+1
(7)2x2 +5x+2 (8)2x2 - 5x+2
(9)2x2-5xy+2y2
(12)(a+b)2 +5(a+b)-36
(11)
(10)6x2 -7xy-5y2
