沪教版(五四学制)七上:9.14 公式法(2)学案(无答案)
文档属性
| 名称 | 沪教版(五四学制)七上:9.14 公式法(2)学案(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 20.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-08 00:00:00 | ||
图片预览

文档简介
9.14(2)公式法——完全平方公式
学习目标:
会用完全平方公式进行因式分解。
会判断一个多项式是不是完全平方式,能把一个多项式配成完全平方式。
学会逆向思维,渗透化归的思想方法。
学习重点:
运用完全平方公式分解因式。
学习难点:
对需要综合运用多种方法的多项式的因式分解。
学习过程:
课前回顾:
1、判断下列多项式能否用平方差公式分解因式?
(1)x2+y2 (2)x2-y2
(3)-x2+y2 (4)-x2-y2
2、分解因式
(1)4-a2b2 (2)2x3-8x
(3)16x4-81
二、新课探索
1、观察:多项式a2+2ab+b2、x2+6x+9、4x2-12xy+9y2有什么特点?
2、
自学检测: (a+b)2=
(a-b)2=
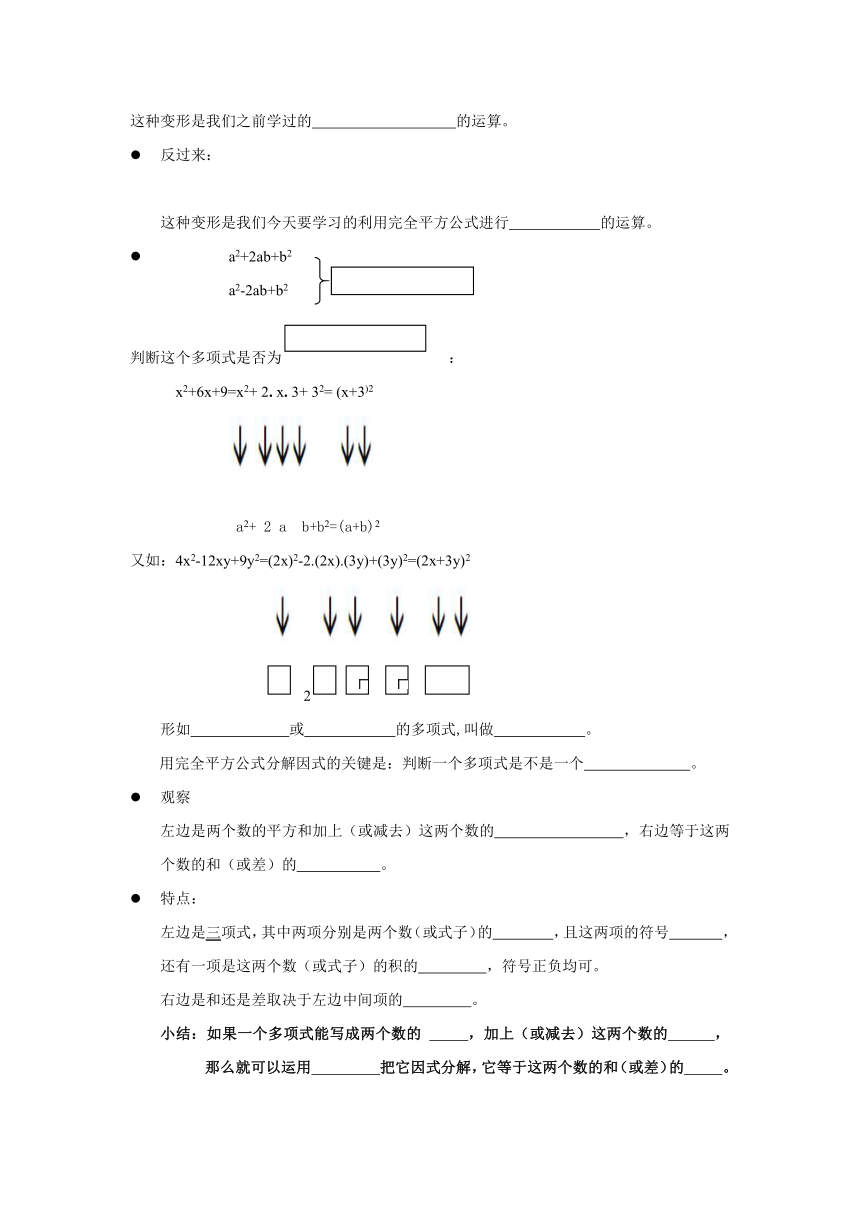
这种变形是我们之前学过的 的运算。
反过来:
这种变形是我们今天要学习的利用完全平方公式进行 的运算。
a2+2ab+b2
a2-2ab+b2
判断这个多项式是否为 :
x2+6x+9=x2+ 2. x. 3+ 32= (x+3)2
a2+ 2 a b+b2=(a+b)2
又如:4x2-12xy+9y2=(2x)2-2.(2x).(3y)+(3y)2=(2x+3y)2
2
形如 或 的多项式,叫做 。
用完全平方公式分解因式的关键是:判断一个多项式是不是一个 。
观察
左边是两个数的平方和加上(或减去)这两个数的 ,右边等于这两个数的和(或差)的 。
特点:
左边是三项式,其中两项分别是两个数(或式子)的 ,且这两项的符号 ,还有一项是这两个数(或式子)的积的 ,符号正负均可。
右边是和还是差取决于左边中间项的 。
小结:如果一个多项式能写成两个数的 ,加上(或减去)这两个数的 ,那么就可以运用 把它因式分解,它等于这两个数的和(或差)的 。
3、巩固练习
分解因式:
(1) x2+12x+36 (2) -2xy-x2-y2
(3) 3ax2+6axy+3ay2 (4) (a+b)2-12(a+b)+36
5、课堂小结
1)如何用符号表示完全平方公式?
(2)完全平方公式的结构特点是什么?
必须是 (或可以看成 的)。
有两个 的平方项。
有一个等于平方项底数的±2倍 项。
6、课后练习
按照完全平方公式填空:
(1)a2-12a+( )=( )2
(2)16-( )+9b2=( )2
(3)( )2+4xy+4=( ) 2
(4)(x-y)2+6(x+y)+( )= ( )2
分解因式
m2+m+
1
4
x2-16xy+64y2
9x+
1
4
+81x2
-m2n2-16+8mn
学习目标:
会用完全平方公式进行因式分解。
会判断一个多项式是不是完全平方式,能把一个多项式配成完全平方式。
学会逆向思维,渗透化归的思想方法。
学习重点:
运用完全平方公式分解因式。
学习难点:
对需要综合运用多种方法的多项式的因式分解。
学习过程:
课前回顾:
1、判断下列多项式能否用平方差公式分解因式?
(1)x2+y2 (2)x2-y2
(3)-x2+y2 (4)-x2-y2
2、分解因式
(1)4-a2b2 (2)2x3-8x
(3)16x4-81
二、新课探索
1、观察:多项式a2+2ab+b2、x2+6x+9、4x2-12xy+9y2有什么特点?
2、
自学检测: (a+b)2=
(a-b)2=
这种变形是我们之前学过的 的运算。
反过来:
这种变形是我们今天要学习的利用完全平方公式进行 的运算。
a2+2ab+b2
a2-2ab+b2
判断这个多项式是否为 :
x2+6x+9=x2+ 2. x. 3+ 32= (x+3)2
a2+ 2 a b+b2=(a+b)2
又如:4x2-12xy+9y2=(2x)2-2.(2x).(3y)+(3y)2=(2x+3y)2
2
形如 或 的多项式,叫做 。
用完全平方公式分解因式的关键是:判断一个多项式是不是一个 。
观察
左边是两个数的平方和加上(或减去)这两个数的 ,右边等于这两个数的和(或差)的 。
特点:
左边是三项式,其中两项分别是两个数(或式子)的 ,且这两项的符号 ,还有一项是这两个数(或式子)的积的 ,符号正负均可。
右边是和还是差取决于左边中间项的 。
小结:如果一个多项式能写成两个数的 ,加上(或减去)这两个数的 ,那么就可以运用 把它因式分解,它等于这两个数的和(或差)的 。
3、巩固练习
分解因式:
(1) x2+12x+36 (2) -2xy-x2-y2
(3) 3ax2+6axy+3ay2 (4) (a+b)2-12(a+b)+36
5、课堂小结
1)如何用符号表示完全平方公式?
(2)完全平方公式的结构特点是什么?
必须是 (或可以看成 的)。
有两个 的平方项。
有一个等于平方项底数的±2倍 项。
6、课后练习
按照完全平方公式填空:
(1)a2-12a+( )=( )2
(2)16-( )+9b2=( )2
(3)( )2+4xy+4=( ) 2
(4)(x-y)2+6(x+y)+( )= ( )2
分解因式
m2+m+
1
4
x2-16xy+64y2
9x+
1
4
+81x2
-m2n2-16+8mn
