沪科版八年级数学上册13.1 三角形中的边角关系课件(2课时共56张)
文档属性
| 名称 | 沪科版八年级数学上册13.1 三角形中的边角关系课件(2课时共56张) |  | |
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-08 19:41:12 | ||
图片预览








文档简介
(共56张PPT)
三角形中的边角关系
本节课的主要内容
1、三角形的定义及其表示方法
2、三角形的元素
3、三角形按边分类
4、三角形的三边关系
5、三角形的稳定性
生活中的三角形
生活中的三角形
生活中的三角形
生活中的三角形
在小学时大家已经初步学过三角形及相关知识,
现在我们进一步系统地研究三角形
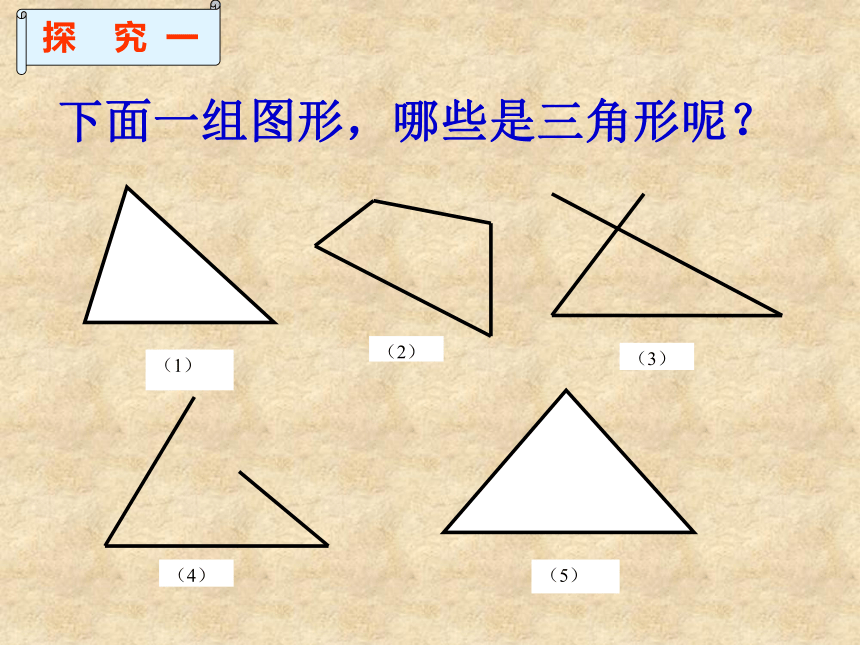
下面一组图形,哪些是三角形呢?
探 究 一
(1)
(2)
(3)
(5)
(4)
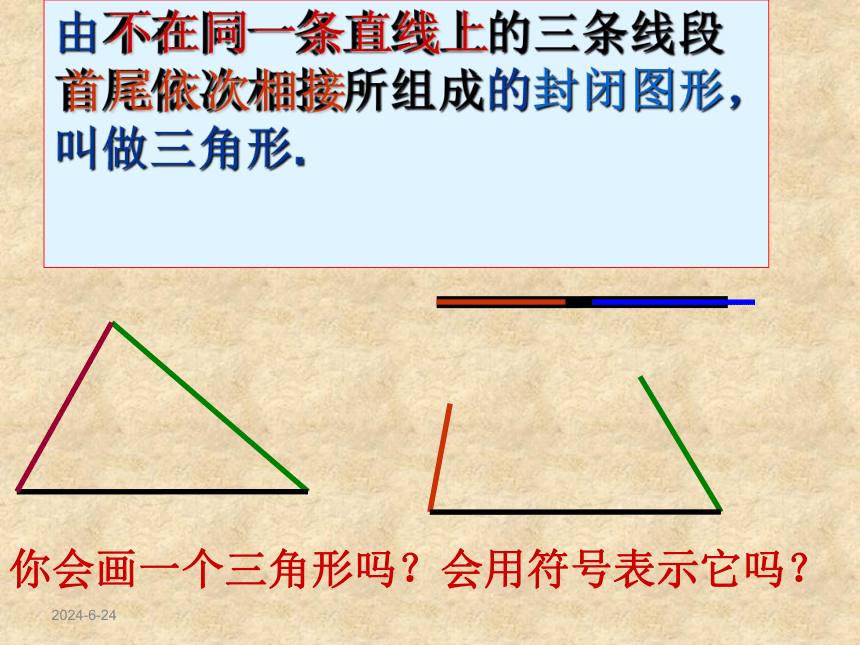
1、三角形的定义
由不在同一条直线上的三条线段首尾依次相接所组成的封闭图形,叫做三角形.
你会画一个三角形吗?会用符号表示它吗?
首尾依次相接
*
不在同一条直线上
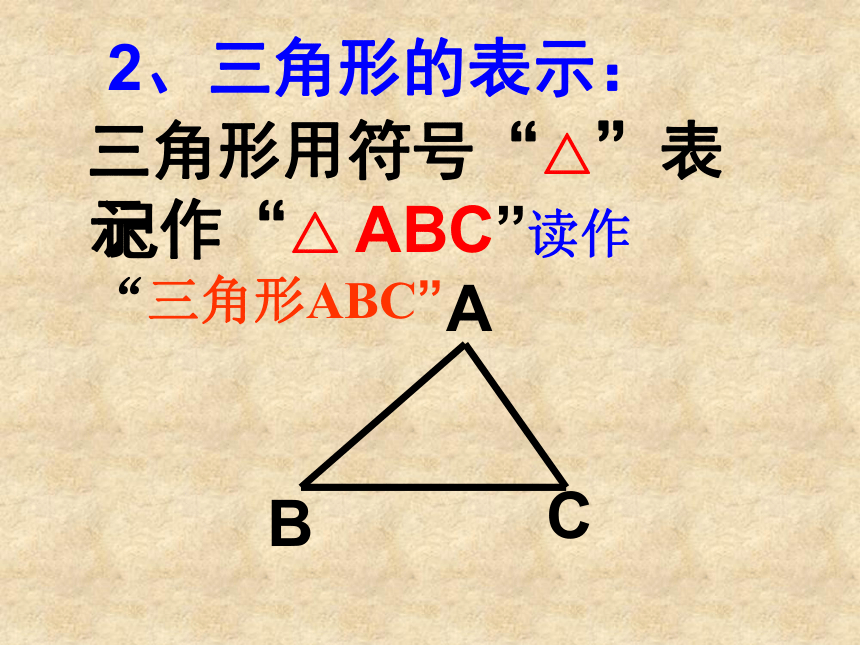
2、三角形的表示:
三角形用符号“△”表示
记作“△ ABC”读作“三角形ABC”
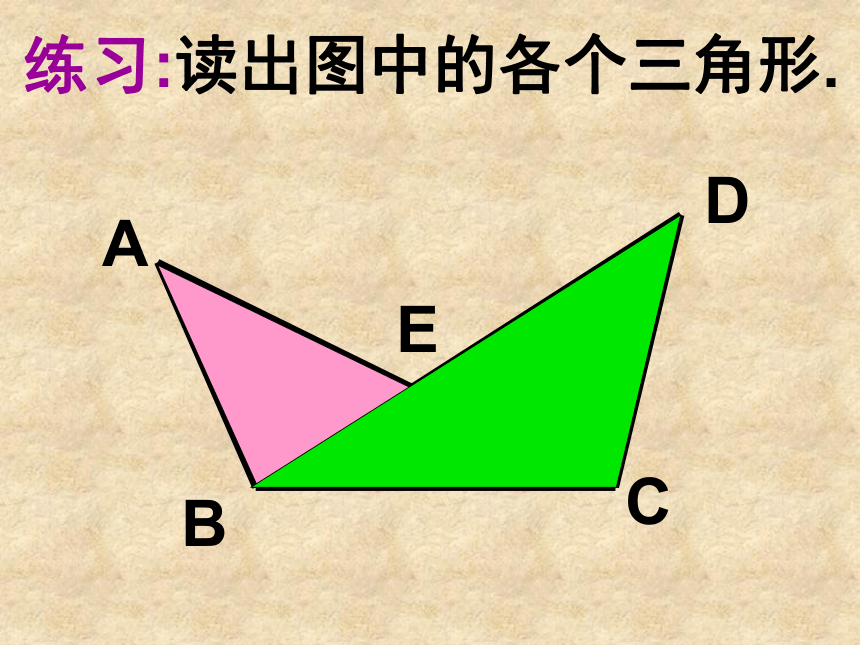
练习:读出图中的各个三角形.
三角形相邻两边的公共端点
叫做三角形的顶点。
如图,三角形ABC有几个顶点?它们分别是
3、三角形的顶点
A
三角形的形状、大小和位置由它的三个顶点确定。
A、B、C
组成三角形的三条线段
叫做三角形的边。
如图,三角形ABC有几条边?它们分别是______________。
4、三角形的边
A
B
C
△ABC的三边,有时也用a、b、c来表示.一般的顶点A所对的边记作a,顶点B所对的边记作b,顶点C所对的边记作c
AB、AC、BC
例 说出图中有多少个三角形,用符号“△”表示,并指出每一个三角形的三条边.
5、三角形的角:
(1)三角形相邻两边所组成的角叫做三角形的内角,简称三角形的角。
(2)三角形的角的一边与另一边的反向延长线组成的角叫做三角形的外角。
)
)
)
)
)
)
E
在 ABC中,AB边所对的角是:
∠A所对的边是:
∠C
BC
★再说几个对边与对角的关系试试。
1.图中有几个三角形?用符号表示这些三角形和各自的边角
2.以AB为边的三角形有哪些?
△ABC、△ABE
3.以E为顶点的三角形有哪些?
△ ABE 、△BCE、 △CDE
练习
4.以∠D为角的三角形有哪些?
△ BCD、 △DEC
A
如图,①图中有几个角是△ABC的外角?说出它们的名称。②∠1、 ∠2是不是△ABC的外角?为什么?
练习
腰
腰
你能找出下列三角形各自的特点吗?
不等边三角形
等腰三角形
等边三角形
三条边各不相等的三角形叫做不等边三角形 .
有两条边相等的三角形叫做等腰三角形
三条边都相等的三角形叫做等边三角形.
底边
顶角
底角
底角
等边三角形和等腰三角形之间有什么关系?
不等边三角形
等腰三角形
于是我们可以把三角形按照三边情况进行分类
腰和底不等的等腰三角形
等边三角形(三边都相等的等腰三角形)
我要到学校可以怎么走呀?哪一条路最近呀?
为什么?
麦
田
蚂蚁从A到B的路线有那些?走哪条路线最近呢?为什么?
A
B
C
路线1:从A到C再到B路线走
路线2:沿线段AB走
请问:路线1、路线2哪条路程较短,你能说出你的根据吗?
两点之间线段最短
三角形任意两边的和大于第三边
想一想,由不等式的变形,三角形的两边之差与第三边有何关系
三角形任意两边的差小于第三边
三角形三边的关系定理的理论根据是?
4、三角形的三边关系定理
两点之间,线段最短
1.下列长度的三条线段能否组成三角形?为什么?
(1) 3,4,8 ( )
(2) 2,5,6 ( )
(3) 5,6,10 ( )
(4) 3,5,8 ( )
不能
能
能
不能
在判断三条线段能否围成一个三角形时,只要判断较小的两条线段之和是否大于最长线段就可以了。
解题技巧:只要比较两条较短线段之和与最长线段
的大小
小颖要制作一个三角形木架,现有两根长度为8cm和5cm的木棒,如果要求第三根木棒的长度是偶数,小颖有几种选法?第三根的长度可以是多少?
∵x为偶数,小颖有5种选法。
第三根木棒的长度可以是:4cm,6cm,8cm,10cm,12cm
解:设第三根木棒长为xcm,有
8-5<x<8+5
3<x<13
分析:第三根木棒不能太短,也不能太长.那么它不能短于几?不能长于几?
3、如果等腰三角形的一边长是4cm,另一边长是9cm,则这个等腰三角形的周长=______________.
2、如果等腰三角形的一边长是5cm,另一边长是8cm,则这个等腰三角形的周长=______________.
1、五条线段的长分别为1cm,2cm,3cm,4cm,5cm,以其中三条线为边长可以构成________个三角形.
3
22cm
18cm或21cm
三边长为:5、5、8和8、8、5
2、3、4,2、4、5,3、4、5
三边长为:4、4、9和4、9、9
123,124,125,134,135,145,234,235,245,345
解题技巧:等腰三角形的模糊说法常要考虑不同情况,并用三角形三边关系定理进行取舍.
有人说,自己步子大,一步能走3米多,你相信吗?说说你的理由!
考考你!
答:不能。如果此人一步能走3米多,由三角形三边的关系得,此人两腿的长的和大于3米多,这与实际情况相矛盾,所以他一步不能走3米多。
草原上的四口油井,位于如图所示的A、B、C、D四个位置,现在要建立一个维修站H,问H建在何处,才能使它到四个油井的距离之和HA+HB+HC+HD为最小?说明理由。
拓展与应用!
A
D
C
B
H
H′
1.你认为这个H应该在什么位置?大胆设想!
2.到A、C距离和最小的点在哪儿?到B、D?
用三根木棒钉一个三角形,你会发现再也无法改变这个
三角形的形状和大小,也就是说,如果一个三角形的
三条边固定了,那么三角形的形状和大小就完全确定了.
在数学上把三角形的这个性质叫做三角形的稳定性.
练一练
1、下列图形中具有稳定性的是( )
(A)正方形 (B)长方形
(C)直角三角形 (D)平行四边形
2、要使下列木架不稳定各至少需要多少根木棍?
C
3、下列图中具有稳定性有( )
A 1个 B 2个 C 3个 D 4个
C
四边形的不稳定性有广泛的应用
课堂小结
1.三角形的概念及其表示方法
2.三角形的元素
3.三角形按边分类
4.三角形三边之间的关系
你都掌握了吗?
5、三角形的稳定性
记一记
三角形的顶点:三角形两边的交点;
点A、点B、点C
三角形的边:组成三角形的线段
边AB、边AC、边BC
或边a、边b、边c
三角形的角:三角形任意两条边所组成的内角,简称三角形的角。
∠A、∠B、∠C
记作:△ABC
三角形九要素:
你能按边长不同说出下列三角形的特点吗?
不等边三角形
等腰三角形
等边三角形
不等边三角形 :三条边互不相等的三角形
等腰三角形:有两条边相等的三角形
等边三角形:三条边都相等的三角形
三角形(按边分)
不等边三角形
等腰三角形
于是我们可以把三角形按照三边情况进行分类
(三边互不相等)
等边三角形
腰和底不等的等腰三角形
三角形三边关系
三角形任意两边之和大于第三边
三角形任意两边之差小于第三边
推理总结:
根据不等式的性质可以得到:
三角形具有稳定性.
*
围一围:
下面有4根木棒,请你任意选三根围一围,可以怎么选?每次都能围成三角形吗?
6cm
8cm
12cm
18cm
探 究 三
实验记录
同位合作: 一人操作,另一人按下表记录结果
能
不能
不能
能
组别 所选小棒的长度(厘米) 能否围成三角形
1 (6) (8) (12)
2 (6) (8) (18)
3 (6) (12) (18)
4 (8) (12) (18)
*
由试验得出结论:
三角形三边的的数量关系是:
较小两条线段的和小于第三边,不能围成三角形。
较小两条线段的和等于第三边,不能围成三角形。
例 :一根木棒长为7,另一根木棒长为2,若要围成三角形,那么则第三根木棒长度应在什么范围呢?
分析:设第三条边长为x
巩固新知
则: 两边之差 < x < 两边之和
(7-2) < x < (7+2)
5 < x < 9
已知:等腰三角形周长为18cm,如果一边长等于4cm,求另两边的长?
解:若底边长为4cm,设腰长为x cm,
则 2x+4=18 解得:x=7
若一条腰长为4cm,设底边长为x cm,则
2×4+x=18 解得:x=10
4+4<10,所以4cm为腰不能构成三角形.
所以,三角形另外两个边长都是7cm
花园里草坪中经常可以看到被人走出一条小路来!
其实我们离文明很近!
4
你能不能运用今天所学的知识解释这一现象?
4米
5米
A
B
C
3米
判断:下列长度的三条线段能否组成三角形?
(1)1cm、2cm、3cm
(2)2cm、3cm、4cm
(3)4cm、5cm、6cm
(4)5cm、6cm、12cm
1、已知三角形三条边都是整数,其中两边长度分别为7cm和2cm,且第三边为奇数,求此第三边。
提高训练
2、等腰三角形的特征就是三角形中有两条边相等,这两条边叫三角形的腰。
(1)已知一个等腰三角形两边长分别是3cm、5cm,求这个三角形的周长?
(2)已知一个等腰三角形两边长分别是2cm、5cm,求这个三角形的周长?
已知三角形三边长分别为
3、a-2、5,
求a的取值范围。
已知AB两个村庄位置如图,今要建一个水厂P,水厂与两个村庄各有一条直线水管相连,问水厂P应建在何处,才能使水厂到两村庄的两条水管总长度PA+PB最短?
A
B
思考讨论
三角形中的边角关系
本节课的主要内容
1、三角形的定义及其表示方法
2、三角形的元素
3、三角形按边分类
4、三角形的三边关系
5、三角形的稳定性
生活中的三角形
生活中的三角形
生活中的三角形
生活中的三角形
在小学时大家已经初步学过三角形及相关知识,
现在我们进一步系统地研究三角形
下面一组图形,哪些是三角形呢?
探 究 一
(1)
(2)
(3)
(5)
(4)
1、三角形的定义
由不在同一条直线上的三条线段首尾依次相接所组成的封闭图形,叫做三角形.
你会画一个三角形吗?会用符号表示它吗?
首尾依次相接
*
不在同一条直线上
2、三角形的表示:
三角形用符号“△”表示
记作“△ ABC”读作“三角形ABC”
练习:读出图中的各个三角形.
三角形相邻两边的公共端点
叫做三角形的顶点。
如图,三角形ABC有几个顶点?它们分别是
3、三角形的顶点
A
三角形的形状、大小和位置由它的三个顶点确定。
A、B、C
组成三角形的三条线段
叫做三角形的边。
如图,三角形ABC有几条边?它们分别是______________。
4、三角形的边
A
B
C
△ABC的三边,有时也用a、b、c来表示.一般的顶点A所对的边记作a,顶点B所对的边记作b,顶点C所对的边记作c
AB、AC、BC
例 说出图中有多少个三角形,用符号“△”表示,并指出每一个三角形的三条边.
5、三角形的角:
(1)三角形相邻两边所组成的角叫做三角形的内角,简称三角形的角。
(2)三角形的角的一边与另一边的反向延长线组成的角叫做三角形的外角。
)
)
)
)
)
)
E
在 ABC中,AB边所对的角是:
∠A所对的边是:
∠C
BC
★再说几个对边与对角的关系试试。
1.图中有几个三角形?用符号表示这些三角形和各自的边角
2.以AB为边的三角形有哪些?
△ABC、△ABE
3.以E为顶点的三角形有哪些?
△ ABE 、△BCE、 △CDE
练习
4.以∠D为角的三角形有哪些?
△ BCD、 △DEC
A
如图,①图中有几个角是△ABC的外角?说出它们的名称。②∠1、 ∠2是不是△ABC的外角?为什么?
练习
腰
腰
你能找出下列三角形各自的特点吗?
不等边三角形
等腰三角形
等边三角形
三条边各不相等的三角形叫做不等边三角形 .
有两条边相等的三角形叫做等腰三角形
三条边都相等的三角形叫做等边三角形.
底边
顶角
底角
底角
等边三角形和等腰三角形之间有什么关系?
不等边三角形
等腰三角形
于是我们可以把三角形按照三边情况进行分类
腰和底不等的等腰三角形
等边三角形(三边都相等的等腰三角形)
我要到学校可以怎么走呀?哪一条路最近呀?
为什么?
麦
田
蚂蚁从A到B的路线有那些?走哪条路线最近呢?为什么?
A
B
C
路线1:从A到C再到B路线走
路线2:沿线段AB走
请问:路线1、路线2哪条路程较短,你能说出你的根据吗?
两点之间线段最短
三角形任意两边的和大于第三边
想一想,由不等式的变形,三角形的两边之差与第三边有何关系
三角形任意两边的差小于第三边
三角形三边的关系定理的理论根据是?
4、三角形的三边关系定理
两点之间,线段最短
1.下列长度的三条线段能否组成三角形?为什么?
(1) 3,4,8 ( )
(2) 2,5,6 ( )
(3) 5,6,10 ( )
(4) 3,5,8 ( )
不能
能
能
不能
在判断三条线段能否围成一个三角形时,只要判断较小的两条线段之和是否大于最长线段就可以了。
解题技巧:只要比较两条较短线段之和与最长线段
的大小
小颖要制作一个三角形木架,现有两根长度为8cm和5cm的木棒,如果要求第三根木棒的长度是偶数,小颖有几种选法?第三根的长度可以是多少?
∵x为偶数,小颖有5种选法。
第三根木棒的长度可以是:4cm,6cm,8cm,10cm,12cm
解:设第三根木棒长为xcm,有
8-5<x<8+5
3<x<13
分析:第三根木棒不能太短,也不能太长.那么它不能短于几?不能长于几?
3、如果等腰三角形的一边长是4cm,另一边长是9cm,则这个等腰三角形的周长=______________.
2、如果等腰三角形的一边长是5cm,另一边长是8cm,则这个等腰三角形的周长=______________.
1、五条线段的长分别为1cm,2cm,3cm,4cm,5cm,以其中三条线为边长可以构成________个三角形.
3
22cm
18cm或21cm
三边长为:5、5、8和8、8、5
2、3、4,2、4、5,3、4、5
三边长为:4、4、9和4、9、9
123,124,125,134,135,145,234,235,245,345
解题技巧:等腰三角形的模糊说法常要考虑不同情况,并用三角形三边关系定理进行取舍.
有人说,自己步子大,一步能走3米多,你相信吗?说说你的理由!
考考你!
答:不能。如果此人一步能走3米多,由三角形三边的关系得,此人两腿的长的和大于3米多,这与实际情况相矛盾,所以他一步不能走3米多。
草原上的四口油井,位于如图所示的A、B、C、D四个位置,现在要建立一个维修站H,问H建在何处,才能使它到四个油井的距离之和HA+HB+HC+HD为最小?说明理由。
拓展与应用!
A
D
C
B
H
H′
1.你认为这个H应该在什么位置?大胆设想!
2.到A、C距离和最小的点在哪儿?到B、D?
用三根木棒钉一个三角形,你会发现再也无法改变这个
三角形的形状和大小,也就是说,如果一个三角形的
三条边固定了,那么三角形的形状和大小就完全确定了.
在数学上把三角形的这个性质叫做三角形的稳定性.
练一练
1、下列图形中具有稳定性的是( )
(A)正方形 (B)长方形
(C)直角三角形 (D)平行四边形
2、要使下列木架不稳定各至少需要多少根木棍?
C
3、下列图中具有稳定性有( )
A 1个 B 2个 C 3个 D 4个
C
四边形的不稳定性有广泛的应用
课堂小结
1.三角形的概念及其表示方法
2.三角形的元素
3.三角形按边分类
4.三角形三边之间的关系
你都掌握了吗?
5、三角形的稳定性
记一记
三角形的顶点:三角形两边的交点;
点A、点B、点C
三角形的边:组成三角形的线段
边AB、边AC、边BC
或边a、边b、边c
三角形的角:三角形任意两条边所组成的内角,简称三角形的角。
∠A、∠B、∠C
记作:△ABC
三角形九要素:
你能按边长不同说出下列三角形的特点吗?
不等边三角形
等腰三角形
等边三角形
不等边三角形 :三条边互不相等的三角形
等腰三角形:有两条边相等的三角形
等边三角形:三条边都相等的三角形
三角形(按边分)
不等边三角形
等腰三角形
于是我们可以把三角形按照三边情况进行分类
(三边互不相等)
等边三角形
腰和底不等的等腰三角形
三角形三边关系
三角形任意两边之和大于第三边
三角形任意两边之差小于第三边
推理总结:
根据不等式的性质可以得到:
三角形具有稳定性.
*
围一围:
下面有4根木棒,请你任意选三根围一围,可以怎么选?每次都能围成三角形吗?
6cm
8cm
12cm
18cm
探 究 三
实验记录
同位合作: 一人操作,另一人按下表记录结果
能
不能
不能
能
组别 所选小棒的长度(厘米) 能否围成三角形
1 (6) (8) (12)
2 (6) (8) (18)
3 (6) (12) (18)
4 (8) (12) (18)
*
由试验得出结论:
三角形三边的的数量关系是:
较小两条线段的和小于第三边,不能围成三角形。
较小两条线段的和等于第三边,不能围成三角形。
例 :一根木棒长为7,另一根木棒长为2,若要围成三角形,那么则第三根木棒长度应在什么范围呢?
分析:设第三条边长为x
巩固新知
则: 两边之差 < x < 两边之和
(7-2) < x < (7+2)
5 < x < 9
已知:等腰三角形周长为18cm,如果一边长等于4cm,求另两边的长?
解:若底边长为4cm,设腰长为x cm,
则 2x+4=18 解得:x=7
若一条腰长为4cm,设底边长为x cm,则
2×4+x=18 解得:x=10
4+4<10,所以4cm为腰不能构成三角形.
所以,三角形另外两个边长都是7cm
花园里草坪中经常可以看到被人走出一条小路来!
其实我们离文明很近!
4
你能不能运用今天所学的知识解释这一现象?
4米
5米
A
B
C
3米
判断:下列长度的三条线段能否组成三角形?
(1)1cm、2cm、3cm
(2)2cm、3cm、4cm
(3)4cm、5cm、6cm
(4)5cm、6cm、12cm
1、已知三角形三条边都是整数,其中两边长度分别为7cm和2cm,且第三边为奇数,求此第三边。
提高训练
2、等腰三角形的特征就是三角形中有两条边相等,这两条边叫三角形的腰。
(1)已知一个等腰三角形两边长分别是3cm、5cm,求这个三角形的周长?
(2)已知一个等腰三角形两边长分别是2cm、5cm,求这个三角形的周长?
已知三角形三边长分别为
3、a-2、5,
求a的取值范围。
已知AB两个村庄位置如图,今要建一个水厂P,水厂与两个村庄各有一条直线水管相连,问水厂P应建在何处,才能使水厂到两村庄的两条水管总长度PA+PB最短?
A
B
思考讨论
