沪科版七年级上数学课件:4.5角的比较与补(余)角(二) (共27张PPT)
文档属性
| 名称 | 沪科版七年级上数学课件:4.5角的比较与补(余)角(二) (共27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 26.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-06 15:45:37 | ||
图片预览





文档简介
(共27张PPT)
第2课时
4.5 角的比较与补(余)角
4.5 角比较与补(余)角
第二课时
余角与补角
知识回顾
1.角的比较两种方法:度量法、叠合法
2.计算角的和与差
3.角的平分线:以角的顶点为端点的一条射线,把这个角分成相等的两个角,这条射线叫做这个角的平分线.
想一想
如图,∠AOB是直角,则∠AOC与∠BOC有怎样的关系?
O
C
B
A
∠AOC+∠BOC=90°
你还能举出一些具有这样关系的角吗?
若∠1=30°,∠2=60°,则∠1+∠2=90°.
若∠α=25°,∠β=65°,则∠α+∠β=90°.
??????
创设情境,引入新知
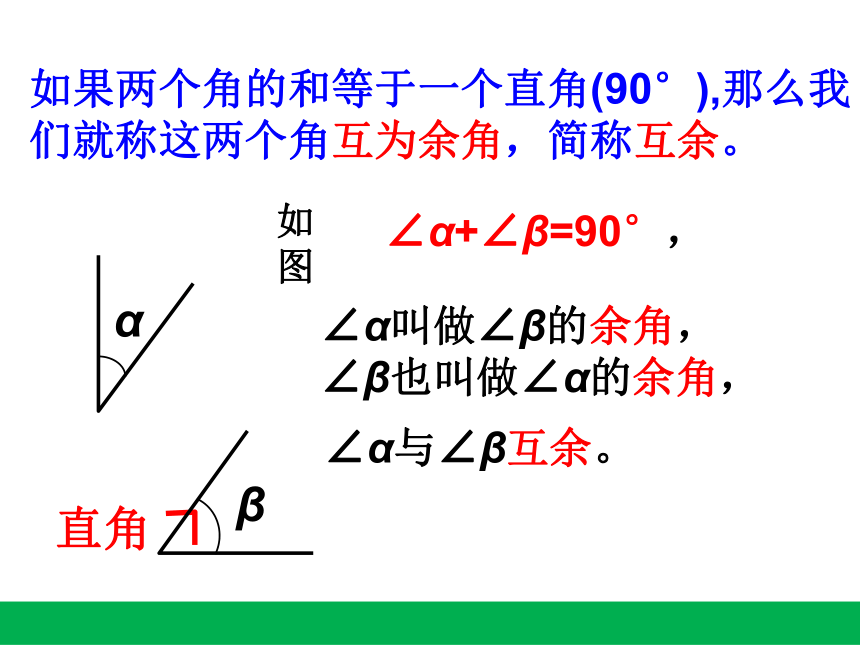
如果两个角的和等于一个直角(90°),那么我们就称这两个角互为余角,简称互余。
α
β
直角
如
图
∠α+∠β=90°,
∠α叫做∠β的余角,
∠β也叫做∠α的余角,
∠α与∠β互余。
想一想
如图,点A,O,B
在同一条直线上,则∠AOC与∠BOC有怎样的关系?
∠AOC+∠BOC=180°
你还能举出一些具有这样关系的角吗?
若∠1=40°,∠2=140°,则∠1+∠2=180°.
若∠α=65°,∠β=115°,则∠α+∠β=180°.
??????
C
A
O
B
?
?
?
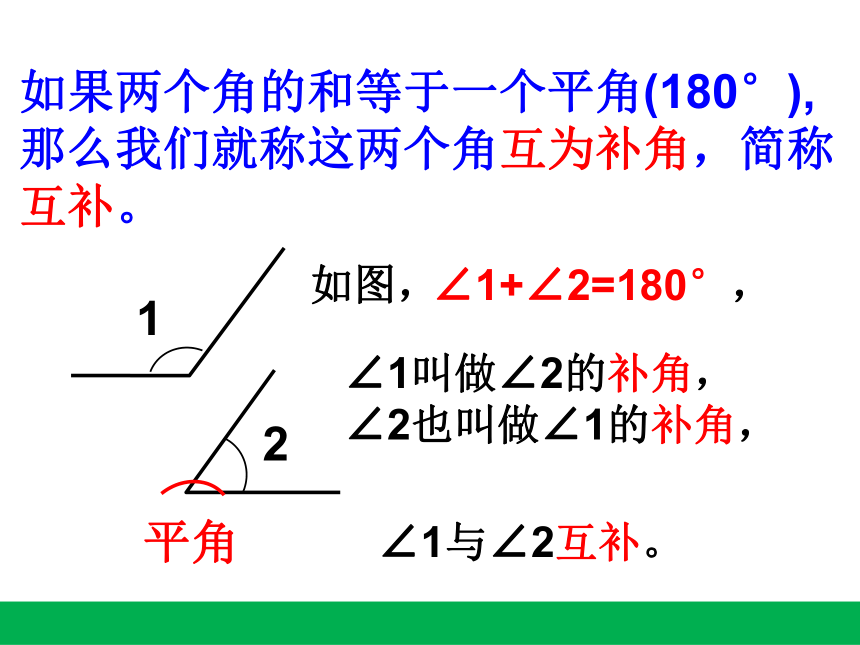
如果两个角的和等于一个平角(180°),那么我们就称这两个角互为补角,简称互补。
1
2
平角
如图,
∠1+∠2=180°,
∠1叫做∠2的补角,
∠2也叫做∠1的补角,
∠1与∠2互补。
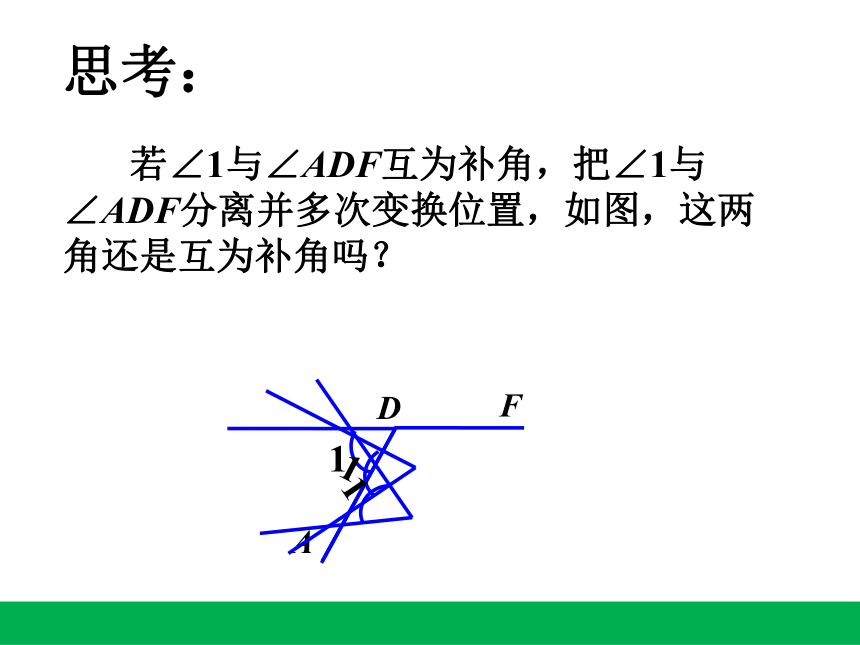
若∠1与∠ADF互为补角,把∠1与∠ADF分离并多次变换位置,如图,这两角还是互为补角吗?
1
A
D
F
1
1
思考:
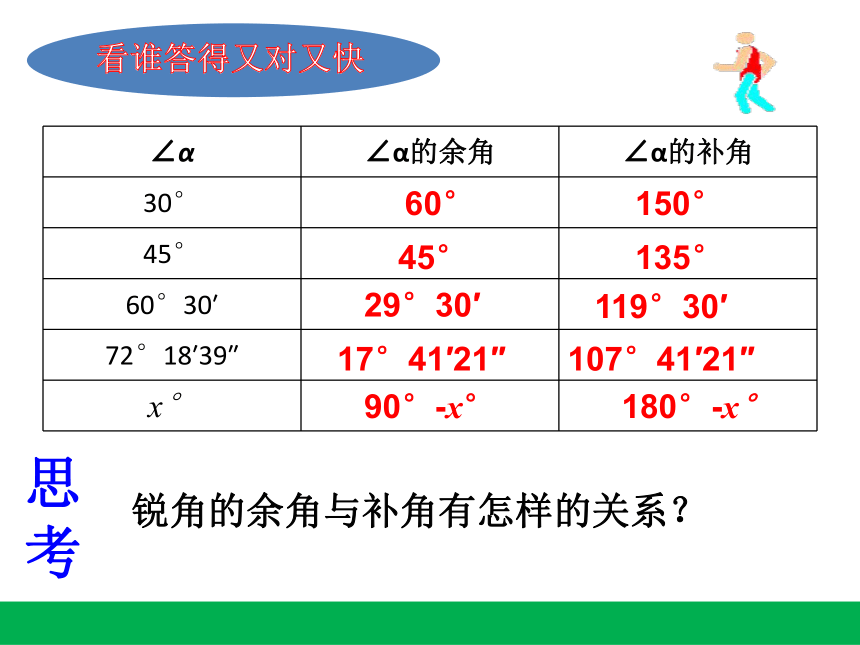
看谁答得又对又快
∠α ∠α的余角 ∠α的补角
30°
45°
60°30′
72°18′39″
x°
90°-x°
180°-x°
107°41′21″
17°41′21″
119°30′
29°30′
135°
45°
150°
60°
思考
锐角的余角与补角有怎样的关系?
(1)若∠1与∠2互补,则∠1+∠2=______.
(2) ∠1=90?-∠2,则∠1与∠2的关系为___________.
180°
互为余角
快速抢答
做一做
已知:一个角的补角加上20°等 于这个角的余角的3倍。
求:这个角的度数。
解
设这个角为x°,
由题意得:
(180-x)+20=3(90-x)
解得:
x=35
答:这个角为35°。
(1)动手画一画:已知,如图,∠α,
请利用三角板画∠α的补角。
图中∠α的补角∠1,∠2的大小有什么关系?为什么?
∵∠1=180°-∠α
∠2=180°-∠α
∴∠1=∠2
这一结论用文字怎么叙述?
同角的补角相等
α
1
2
图中∠α的补角为∠1,∠2。
自主探究
∵∠1=180°-∠α
∠2=180°-∠β
∴∠1=∠2
这一结论用文字又怎么叙述?
等角的补角相等
如图,∠α=∠β,∠α的补角∠1,∠β的补角∠2的大小有什么关系?为什么?
β
α
2
1
又∵∠α=∠β
自主探究
(1)动手画一画:已知,如图,∠α,
请利用三角板画∠α的余角。
图中∠α的余角∠1,∠2的大小有什么关系?为什么?
∵∠1=90°-∠α
∠2=90°-∠α
∴∠1=∠2
这一结论用文字又怎么叙述?
同角的余角相等
α
1
2
图中∠α的余角为∠1,∠2。
自主探究
∵∠1=90°-∠α
∠2=90°-∠β
∴∠1=∠2
这一结论用文字又怎么叙述?
等角的余角相等
如图,∠α=∠β,∠α的余角∠1,∠β的余角∠2的大小有什么关系?为什么?
β
α
2
1
又∵∠α=∠β
自主探究
同角(或等角)的补角相等;
同角(或等角)的余角相等。
归纳
补角和余角的性质
(1)若∠1与∠2互余,∠2与∠3互余, 则_____=______,根据是________.
(2)若∠3与∠4互补,∠6与∠5互补,且∠3=∠6, 则_____=______,根据是__________.
同角的余角相等
等角的补角相等
∠1
∠3
∠4
∠5
1.填空.
课堂练习
2.判断题
(1)一个角的余角一定比这个角的补角小。 ( )
(2)若? AOB与? BOC互补,则A、O、C同在一直线上。 ( )
(3)若∠1+∠2+∠3=180°,那么∠1、∠2、∠3互为补角。 ( )
数学小知识
打台球时,球的反射角总是等于入射角.
入射角
反射角
O
创设情境,引入新知
学以致用:如果∠5=40°,那么∠1应等于多少度,才能保证蓝色球准确入袋?请说明理由.
仔细找一找
A
D
C
O
E
B
1.如图,点A,O,B在同一条直线上,∠AOC=∠DOE=90°,找出图中相等的角,互余的角,互补的角。
解 相等的角有:∠AOC=∠BOC=∠DOE,∠AOD=∠COE,∠DOC=∠BOE;
互余的角 有:
∠AOD和∠DOC,∠AOD和∠BOE,
∠COE和∠DOE,∠COE和∠BOE;
互补的角 有:
∠AOD和∠DOB,∠AOE和∠BOE,
∠COE和∠DOB,∠AOE和∠DOC.
C
A
D
O
E
B
2.如图,点A,O,B在同一条直线上,∠AOC=∠DOE=90°,若∠1=2∠3,求∠2的度数。
试一试
A
D
C
O
E
B
1
3
2
解
设∠3=x°,则∠1=2x°
∵∠1+∠DOE+∠3=180°
∴2x°+90°+x°=180°
解得 x°=30° 即∠3=30°
又∵∠2+∠COE=90°∠3+∠COE=90°
∴∠2=∠3
∴∠2=30°
答:∠2为30°。
(同角的余角相等)
C
A
D
O
E
B
1
2
3
谈谈你有哪些收获?
互为余角 互为补角
对应图形
数量关系
性 质
1
2
1
2
∠1+ ∠2 = 90 °
∠1+ ∠2 = 180 °
同角或等角的余角相等.
同角或等角的补角相等.
课堂总结
完成教材第151页习题4.5第6,7题
布置作业
第2课时
4.5 角的比较与补(余)角
4.5 角比较与补(余)角
第二课时
余角与补角
知识回顾
1.角的比较两种方法:度量法、叠合法
2.计算角的和与差
3.角的平分线:以角的顶点为端点的一条射线,把这个角分成相等的两个角,这条射线叫做这个角的平分线.
想一想
如图,∠AOB是直角,则∠AOC与∠BOC有怎样的关系?
O
C
B
A
∠AOC+∠BOC=90°
你还能举出一些具有这样关系的角吗?
若∠1=30°,∠2=60°,则∠1+∠2=90°.
若∠α=25°,∠β=65°,则∠α+∠β=90°.
??????
创设情境,引入新知
如果两个角的和等于一个直角(90°),那么我们就称这两个角互为余角,简称互余。
α
β
直角
如
图
∠α+∠β=90°,
∠α叫做∠β的余角,
∠β也叫做∠α的余角,
∠α与∠β互余。
想一想
如图,点A,O,B
在同一条直线上,则∠AOC与∠BOC有怎样的关系?
∠AOC+∠BOC=180°
你还能举出一些具有这样关系的角吗?
若∠1=40°,∠2=140°,则∠1+∠2=180°.
若∠α=65°,∠β=115°,则∠α+∠β=180°.
??????
C
A
O
B
?
?
?
如果两个角的和等于一个平角(180°),那么我们就称这两个角互为补角,简称互补。
1
2
平角
如图,
∠1+∠2=180°,
∠1叫做∠2的补角,
∠2也叫做∠1的补角,
∠1与∠2互补。
若∠1与∠ADF互为补角,把∠1与∠ADF分离并多次变换位置,如图,这两角还是互为补角吗?
1
A
D
F
1
1
思考:
看谁答得又对又快
∠α ∠α的余角 ∠α的补角
30°
45°
60°30′
72°18′39″
x°
90°-x°
180°-x°
107°41′21″
17°41′21″
119°30′
29°30′
135°
45°
150°
60°
思考
锐角的余角与补角有怎样的关系?
(1)若∠1与∠2互补,则∠1+∠2=______.
(2) ∠1=90?-∠2,则∠1与∠2的关系为___________.
180°
互为余角
快速抢答
做一做
已知:一个角的补角加上20°等 于这个角的余角的3倍。
求:这个角的度数。
解
设这个角为x°,
由题意得:
(180-x)+20=3(90-x)
解得:
x=35
答:这个角为35°。
(1)动手画一画:已知,如图,∠α,
请利用三角板画∠α的补角。
图中∠α的补角∠1,∠2的大小有什么关系?为什么?
∵∠1=180°-∠α
∠2=180°-∠α
∴∠1=∠2
这一结论用文字怎么叙述?
同角的补角相等
α
1
2
图中∠α的补角为∠1,∠2。
自主探究
∵∠1=180°-∠α
∠2=180°-∠β
∴∠1=∠2
这一结论用文字又怎么叙述?
等角的补角相等
如图,∠α=∠β,∠α的补角∠1,∠β的补角∠2的大小有什么关系?为什么?
β
α
2
1
又∵∠α=∠β
自主探究
(1)动手画一画:已知,如图,∠α,
请利用三角板画∠α的余角。
图中∠α的余角∠1,∠2的大小有什么关系?为什么?
∵∠1=90°-∠α
∠2=90°-∠α
∴∠1=∠2
这一结论用文字又怎么叙述?
同角的余角相等
α
1
2
图中∠α的余角为∠1,∠2。
自主探究
∵∠1=90°-∠α
∠2=90°-∠β
∴∠1=∠2
这一结论用文字又怎么叙述?
等角的余角相等
如图,∠α=∠β,∠α的余角∠1,∠β的余角∠2的大小有什么关系?为什么?
β
α
2
1
又∵∠α=∠β
自主探究
同角(或等角)的补角相等;
同角(或等角)的余角相等。
归纳
补角和余角的性质
(1)若∠1与∠2互余,∠2与∠3互余, 则_____=______,根据是________.
(2)若∠3与∠4互补,∠6与∠5互补,且∠3=∠6, 则_____=______,根据是__________.
同角的余角相等
等角的补角相等
∠1
∠3
∠4
∠5
1.填空.
课堂练习
2.判断题
(1)一个角的余角一定比这个角的补角小。 ( )
(2)若? AOB与? BOC互补,则A、O、C同在一直线上。 ( )
(3)若∠1+∠2+∠3=180°,那么∠1、∠2、∠3互为补角。 ( )
数学小知识
打台球时,球的反射角总是等于入射角.
入射角
反射角
O
创设情境,引入新知
学以致用:如果∠5=40°,那么∠1应等于多少度,才能保证蓝色球准确入袋?请说明理由.
仔细找一找
A
D
C
O
E
B
1.如图,点A,O,B在同一条直线上,∠AOC=∠DOE=90°,找出图中相等的角,互余的角,互补的角。
解 相等的角有:∠AOC=∠BOC=∠DOE,∠AOD=∠COE,∠DOC=∠BOE;
互余的角 有:
∠AOD和∠DOC,∠AOD和∠BOE,
∠COE和∠DOE,∠COE和∠BOE;
互补的角 有:
∠AOD和∠DOB,∠AOE和∠BOE,
∠COE和∠DOB,∠AOE和∠DOC.
C
A
D
O
E
B
2.如图,点A,O,B在同一条直线上,∠AOC=∠DOE=90°,若∠1=2∠3,求∠2的度数。
试一试
A
D
C
O
E
B
1
3
2
解
设∠3=x°,则∠1=2x°
∵∠1+∠DOE+∠3=180°
∴2x°+90°+x°=180°
解得 x°=30° 即∠3=30°
又∵∠2+∠COE=90°∠3+∠COE=90°
∴∠2=∠3
∴∠2=30°
答:∠2为30°。
(同角的余角相等)
C
A
D
O
E
B
1
2
3
谈谈你有哪些收获?
互为余角 互为补角
对应图形
数量关系
性 质
1
2
1
2
∠1+ ∠2 = 90 °
∠1+ ∠2 = 180 °
同角或等角的余角相等.
同角或等角的补角相等.
课堂总结
完成教材第151页习题4.5第6,7题
布置作业
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
