沪科版九年级数学下册第24章 圆24.7 .1弧长与扇形面积课件(第1课时) (共22张PPT)
文档属性
| 名称 | 沪科版九年级数学下册第24章 圆24.7 .1弧长与扇形面积课件(第1课时) (共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1003.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-08 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
24.7 弧长和扇形面积(第1课时)
九年级 下册
B
O
A
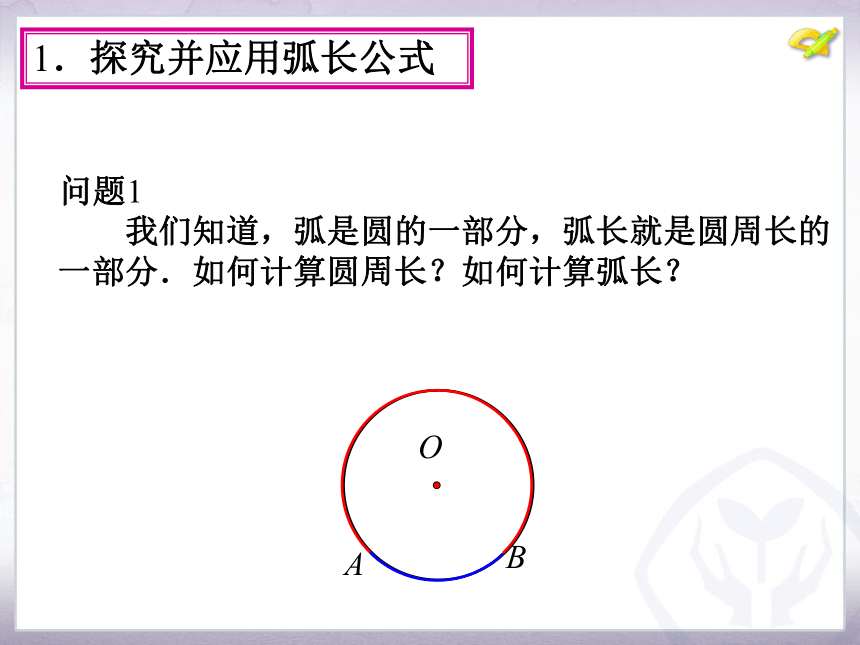
问题1 我们知道,弧是圆的一部分,弧长就是圆周长的一部分.如何计算圆周长?如何计算弧长?
1.探究并应用弧长公式
1.探究并应用弧长公式
问题1 我们知道,弧是圆的一部分,弧长就是圆周长的一部分.如何计算圆周长?如何计算弧长?
问题1 (1)圆的周长可以看作是多少度的圆心角所对的 弧长?
(2) 1°的圆心角所对的弧长是多少?
2°的圆心角所对 的弧长?
5°的圆心角所对 的弧长?
1.探究并应用弧长公式
追问1 怎样计算半径为 R 的圆中,n°的圆心角所对的弧长?
1.探究并应用弧长公式
.
追问2 弧长的大小由哪些量决定?
圆的大小(半径)、圆心角的度数.
1.探究并应用弧长公式
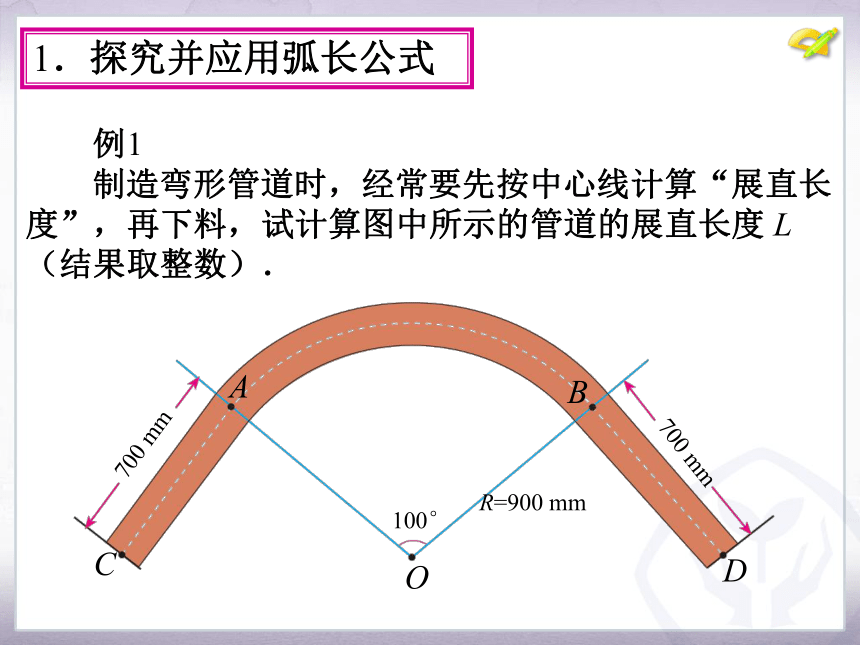
例1 制造弯形管道时,经常要先按中心线计算“展直长 度”,再下料,试计算图中所示的管道的展直长度 L (结果取整数).
1.探究并应用弧长公式
100°
计算上图展直长度:
因此所要求的展直长度:
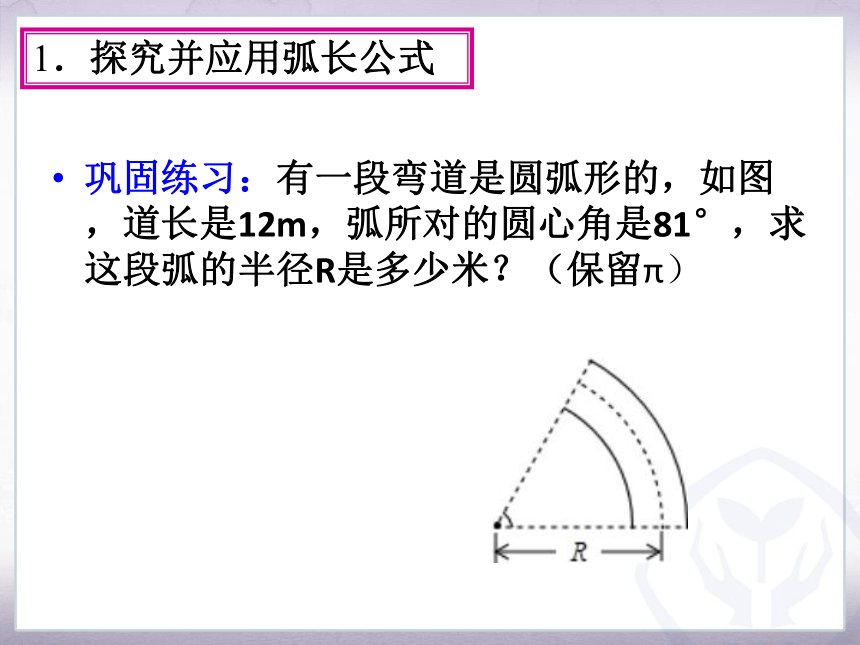
巩固练习:有一段弯道是圆弧形的,如图,道长是12m,弧所对的圆心角是81°,求这段弧的半径R是多少米?(保留π)
1.探究并应用弧长公式
2.探究并应用扇形面积公式
问题2 同学们已经学习了扇形:由组成圆心角的两条半径 和圆心角所对的弧所围成的图形叫做扇形.你能否类比 刚才我们研究弧长公式的方法推导出扇形面积的计算公式?
想一想:扇形的面积与什么有关?
讨论:怎样从圆的面积公式中找出扇形的面积与扇形的圆心角、半径之间的关系?
2.探究并应用扇形面积公式
从而得出:半径为R,圆心角为n?的扇形的面积是
比一比: n?的圆心角所对的弧长和扇形的面积之间有什么关系?
学科网
2.探究并应用扇形面积公式
例2.
(1)
(1)截面上有水部分的面积是指图上哪一部分?
思考:
2.探究并应用扇形面积公式
如图,水平放置的圆柱形排水管道的截面半径是0.6 m,其中水面高 0.3 m,求截面上有水部分的面积(结果保留小数点后两位).
D
(2)
(3)
讨论:
(2)水面高0.3 m是指哪一条线段的长
(如图(2))?这条线段应该怎样画出来?
(3)要求图中阴影部分 面积,应该怎么办?
2.探究并应用扇形面积公式
思考:
(4)要求扇形OAB的面积,需要知道哪些量?这些量能求出来吗?
(5)要求△OAB的面积,需要知道哪些量?这些量能求出来吗?
2.探究并应用扇形面积公式
例2 如图,水平放置的圆柱形排水管道的截面半径是
0.6 m,其中水面高 0.3 m,求截面上有水部分的面积(结果保留小数点后两位).
2.探究并应用扇形面积公式
解:如图24.4-3,连接OA,OB,过点O作弦AB的垂线,垂足为D,交AB于点C,连接AC.
∵ OC=0.6, DC=0.3,
∴ OD=OC- DC=0.3,
∴ OD=DC.
又 AD ⊥DC,
∴AD是线段OC的垂直平分线,
∴AC=AO=OC.
从而 ∠AOD=60?, ∠AOB=120?.
有水部分的面积:
S=S扇形OAB - S ΔOAB
3、巩固练习
1.一个扇形的圆心角是120 ° ,它的面积是3πcm2 ,则这个扇形的半径是( ) A.3πcm B. 3cm C. 6cm D.9cm
2.若扇形的弧长是16cm ,面积是56cm2 ,则它的半径是( )
A.7cm B. 3.5cm C. 2.8cm D.14cm
3.已知⊙O的半径OA=6,扇形OAB的弧长等于4π,则扇形所对的圆心角的度数是( )
A.120° B. 90 ° C.30 ° D.60 °
B
A
A
4、小结提高
( 2).思考:如何求下列两个图中阴影部分的面积?
图(1)的阴影面积=扇形OAB的面积+ △OAB的面积
图(2)的阴影面积=扇形OAB的面积- △OAB的面积
教科书习题 24.4 第 4,6,8 题.
5.布置作业
24.7 弧长和扇形面积(第1课时)
九年级 下册
B
O
A
问题1 我们知道,弧是圆的一部分,弧长就是圆周长的一部分.如何计算圆周长?如何计算弧长?
1.探究并应用弧长公式
1.探究并应用弧长公式
问题1 我们知道,弧是圆的一部分,弧长就是圆周长的一部分.如何计算圆周长?如何计算弧长?
问题1 (1)圆的周长可以看作是多少度的圆心角所对的 弧长?
(2) 1°的圆心角所对的弧长是多少?
2°的圆心角所对 的弧长?
5°的圆心角所对 的弧长?
1.探究并应用弧长公式
追问1 怎样计算半径为 R 的圆中,n°的圆心角所对的弧长?
1.探究并应用弧长公式
.
追问2 弧长的大小由哪些量决定?
圆的大小(半径)、圆心角的度数.
1.探究并应用弧长公式
例1 制造弯形管道时,经常要先按中心线计算“展直长 度”,再下料,试计算图中所示的管道的展直长度 L (结果取整数).
1.探究并应用弧长公式
100°
计算上图展直长度:
因此所要求的展直长度:
巩固练习:有一段弯道是圆弧形的,如图,道长是12m,弧所对的圆心角是81°,求这段弧的半径R是多少米?(保留π)
1.探究并应用弧长公式
2.探究并应用扇形面积公式
问题2 同学们已经学习了扇形:由组成圆心角的两条半径 和圆心角所对的弧所围成的图形叫做扇形.你能否类比 刚才我们研究弧长公式的方法推导出扇形面积的计算公式?
想一想:扇形的面积与什么有关?
讨论:怎样从圆的面积公式中找出扇形的面积与扇形的圆心角、半径之间的关系?
2.探究并应用扇形面积公式
从而得出:半径为R,圆心角为n?的扇形的面积是
比一比: n?的圆心角所对的弧长和扇形的面积之间有什么关系?
学科网
2.探究并应用扇形面积公式
例2.
(1)
(1)截面上有水部分的面积是指图上哪一部分?
思考:
2.探究并应用扇形面积公式
如图,水平放置的圆柱形排水管道的截面半径是0.6 m,其中水面高 0.3 m,求截面上有水部分的面积(结果保留小数点后两位).
D
(2)
(3)
讨论:
(2)水面高0.3 m是指哪一条线段的长
(如图(2))?这条线段应该怎样画出来?
(3)要求图中阴影部分 面积,应该怎么办?
2.探究并应用扇形面积公式
思考:
(4)要求扇形OAB的面积,需要知道哪些量?这些量能求出来吗?
(5)要求△OAB的面积,需要知道哪些量?这些量能求出来吗?
2.探究并应用扇形面积公式
例2 如图,水平放置的圆柱形排水管道的截面半径是
0.6 m,其中水面高 0.3 m,求截面上有水部分的面积(结果保留小数点后两位).
2.探究并应用扇形面积公式
解:如图24.4-3,连接OA,OB,过点O作弦AB的垂线,垂足为D,交AB于点C,连接AC.
∵ OC=0.6, DC=0.3,
∴ OD=OC- DC=0.3,
∴ OD=DC.
又 AD ⊥DC,
∴AD是线段OC的垂直平分线,
∴AC=AO=OC.
从而 ∠AOD=60?, ∠AOB=120?.
有水部分的面积:
S=S扇形OAB - S ΔOAB
3、巩固练习
1.一个扇形的圆心角是120 ° ,它的面积是3πcm2 ,则这个扇形的半径是( ) A.3πcm B. 3cm C. 6cm D.9cm
2.若扇形的弧长是16cm ,面积是56cm2 ,则它的半径是( )
A.7cm B. 3.5cm C. 2.8cm D.14cm
3.已知⊙O的半径OA=6,扇形OAB的弧长等于4π,则扇形所对的圆心角的度数是( )
A.120° B. 90 ° C.30 ° D.60 °
B
A
A
4、小结提高
( 2).思考:如何求下列两个图中阴影部分的面积?
图(1)的阴影面积=扇形OAB的面积+ △OAB的面积
图(2)的阴影面积=扇形OAB的面积- △OAB的面积
教科书习题 24.4 第 4,6,8 题.
5.布置作业
