湘教版数学九年级下册第1章 二次函数本章复习与测试 (含答案)
文档属性
| 名称 | 湘教版数学九年级下册第1章 二次函数本章复习与测试 (含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 225.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-06 00:00:00 | ||
图片预览


文档简介
2019—2020学年湘教版九年级数学下册第1章《二次函数》培优试题与简答
一.选择题(共10小题,每小题3分,共30分)
1.二次函数y=2x2﹣3的二次项系数、一次项系数和常数项分別是( )
A.2、0、﹣3 B.2、﹣3、0 C.2、3、0 D.2、0、3
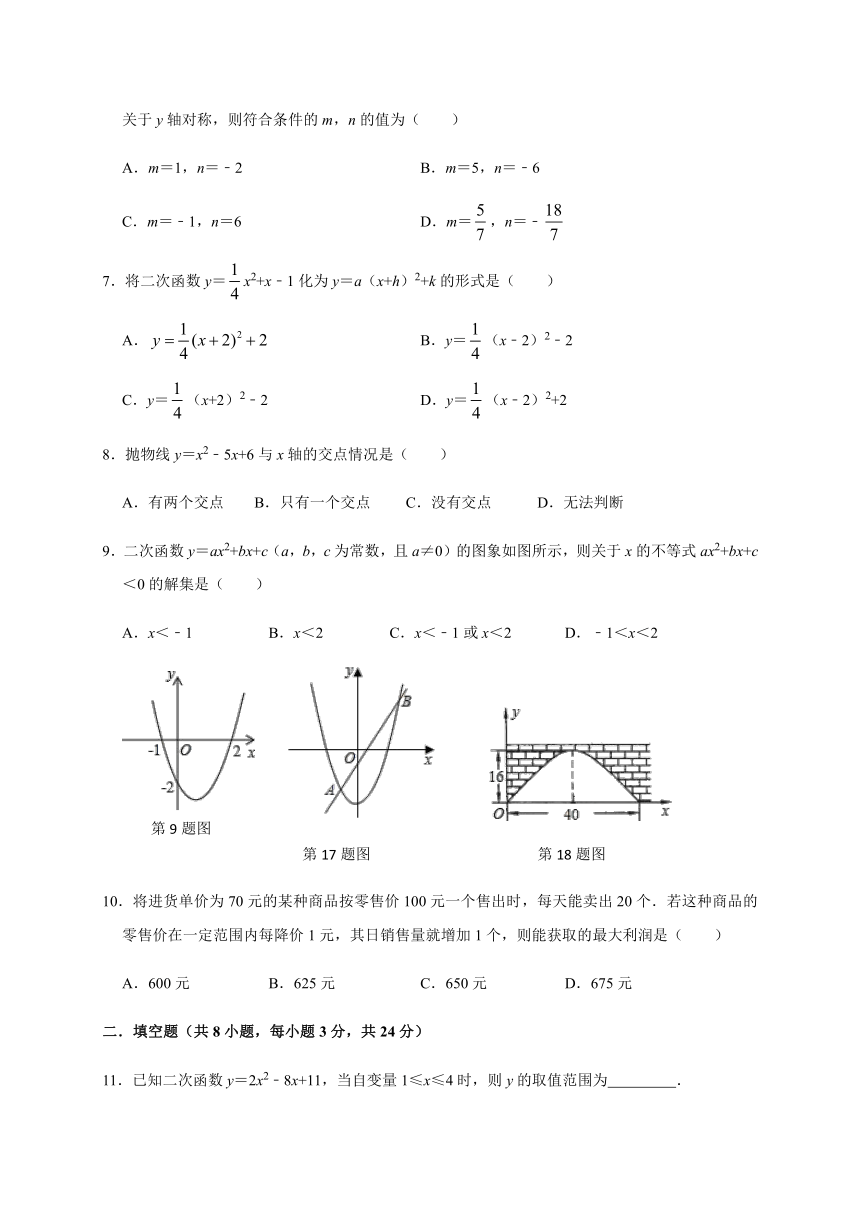
2.已知关于x的二次函数y=kx2﹣bx+1的图象如图所示,则关于x的一次函数y=kx+b的图象不经过哪个象限( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.下列对二次函数y=x2﹣x的图象的描述,正确的是( )
A.开口向下 B.对称轴是y轴
C.当x=时,y有最小值是﹣ D.在对称轴左侧y随x的增大而增大
4.已知二次函数的图象如图所示,下列结论:①abc>0;②;③2a+b=0;④a﹣b+c<0.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
5.点(5,3)在抛物线y=a(x﹣2)2+k上,则下列的点也一定在抛物线上的是( )
A.(﹣5,3) B.(﹣1,3) C.(﹣9,3) D.(1,3)
6.在同一平面直角坐标系中,若抛物线y=x2+(2m﹣1)x+2m﹣4与抛物线y=x2﹣(3m+n)x+n关于y轴对称,则符合条件的m,n的值为( )
A.m=1,n=﹣2 B.m=5,n=﹣6
C.m=﹣1,n=6 D.m=,n=﹣
7.将二次函数y=x2+x﹣1化为y=a(x+h)2+k的形式是( )
A. B.y=(x﹣2)2﹣2
C.y=(x+2)2﹣2 D.y=(x﹣2)2+2
8.抛物线y=x2﹣5x+6与x轴的交点情况是( )
A.有两个交点 B.只有一个交点 C.没有交点 D.无法判断
9.二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)的图象如图所示,则关于x的不等式ax2+bx+c<0的解集是( )
A.x<﹣1 B.x<2 C.x<﹣1或x<2 D.﹣1<x<2
10.将进货单价为70元的某种商品按零售价100元一个售出时,每天能卖出20个.若这种商品的零售价在一定范围内每降价1元,其日销售量就增加1个,则能获取的最大利润是( )
A.600元 B.625元 C.650元 D.675元
二.填空题(共8小题,每小题3分,共24分)
11.已知二次函数y=2x2﹣8x+11,当自变量1≤x≤4时,则y的取值范围为 .
12.若二次函数y=x2+2x+m的图象与坐标轴有3个交点,则m的取值范围是 .
13.若点A(﹣3,n)、B(m,n)在二次函数y=3(x+2)2+k的图象上,则m的值为 .
14.把抛物线y=﹣x2+4x﹣3先向左平移3个单位,再向下平移2个单位,则变换后的抛物线解析式是 .
15.已知实数x、y满足x2+x﹣y+2=0,则x+y的最小值为 .
16.抛物线y=x2﹣3x﹣1010与x轴的其中一个交点是(m,0),则2m2﹣6m的值为 .
17.如图,抛物线y=ax2+c与直线y=mx+n交于A(﹣1,p),B(3,q)两点,则不等式ax2+mx+c<n的解集是 .
18.如图,有一座拱桥洞呈抛物线形状,这个桥洞的最大高度为16m,跨度为40m,现把它的示意图放在如图的平面直角坐标系中,则抛物线对应的函数关系式为 .
三.解答题(共5小题,满分46分,其中19、20每小题8分,21、22、23每小题10分)
19.二次函数y=x2﹣2x﹣8.
(1)将y=x2﹣2x﹣8用配方法化成y=a(x﹣h)2+k的形式,并写出顶点坐标;
(2)求此函数图象与x轴、y轴的交点坐标.
20.用长为6米的铝合金条制成如图所示的窗框,若窗框的高为x米,窗户的透光面积为S平方米(铝合金条的宽度不计).
(1)S与x之间的函数关系式为 ,自变量x的取值范围为 ;
(2)如何安排窗框的高和宽,才能使窗户的透光面积最大?最大面积是多少?
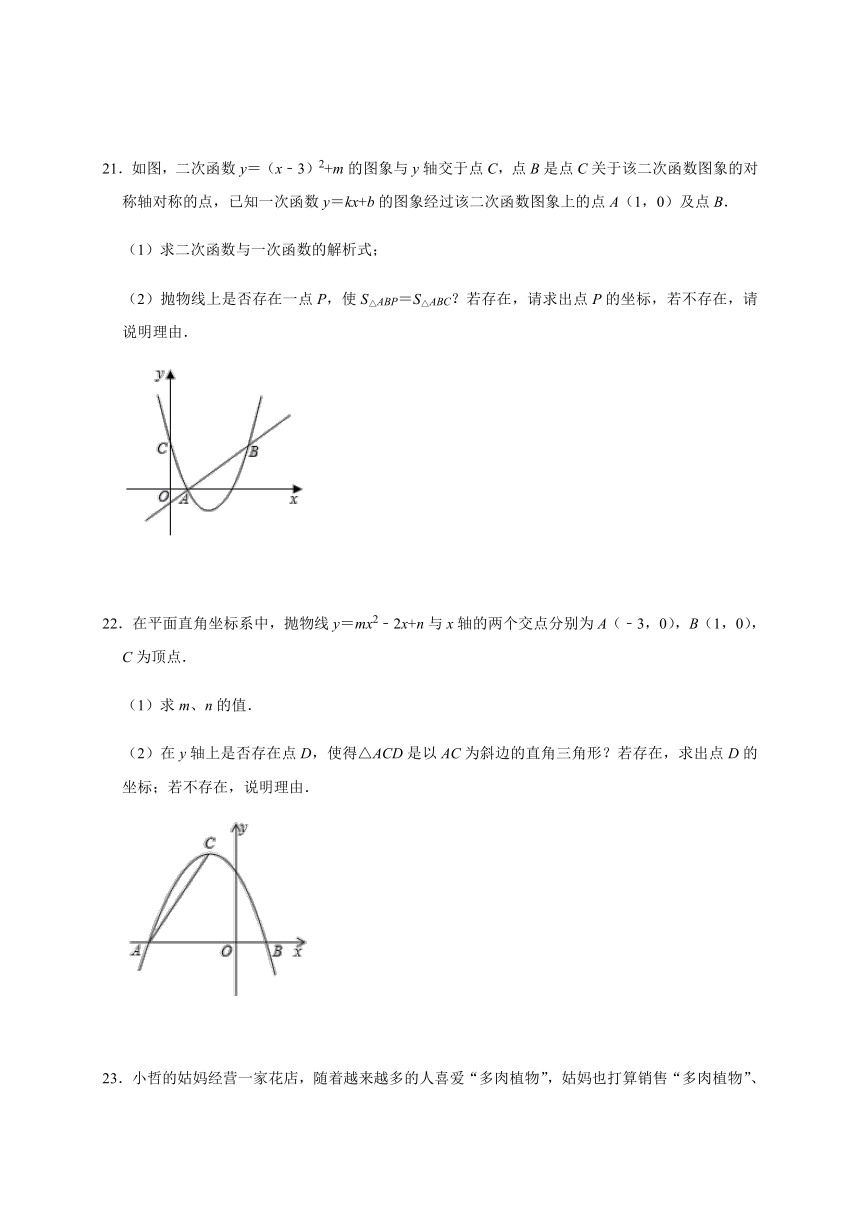
21.如图,二次函数y=(x﹣3)2+m的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点,已知一次函数y=kx+b的图象经过该二次函数图象上的点A(1,0)及点B.
(1)求二次函数与一次函数的解析式;
(2)抛物线上是否存在一点P,使S△ABP=S△ABC?若存在,请求出点P的坐标,若不存在,请说明理由.
22.在平面直角坐标系中,抛物线y=mx2﹣2x+n与x轴的两个交点分别为A(﹣3,0),B(1,0),C为顶点.
(1)求m、n的值.
(2)在y轴上是否存在点D,使得△ACD是以AC为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由.
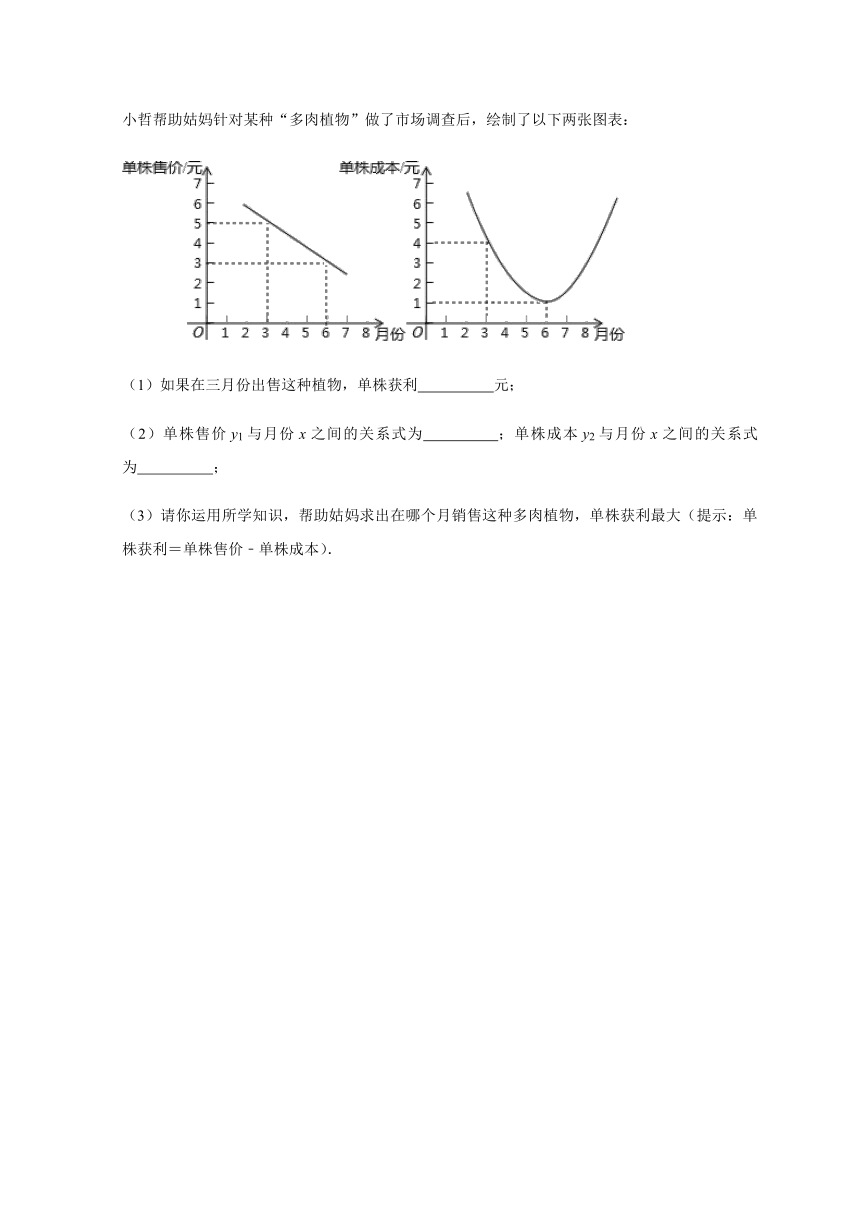
23.小哲的姑妈经营一家花店,随着越来越多的人喜爱“多肉植物”,姑妈也打算销售“多肉植物”、小哲帮助姑妈针对某种“多肉植物”做了市场调查后,绘制了以下两张图表:
(1)如果在三月份出售这种植物,单株获利 元;
(2)单株售价y1与月份x之间的关系式为 ;单株成本y2与月份x之间的关系式为 ;
(3)请你运用所学知识,帮助姑妈求出在哪个月销售这种多肉植物,单株获利最大(提示:单株获利=单株售价﹣单株成本).
2019—2020学年湘教版九年级数学下册第1章《二次函数》培优试题参考简答
一.选择题(共10小题)
1.A. 2.B. 3.C. 4.C. 5.B. 6.A. 7.C. 8.A.
9.D. 10.B.
二.填空题(共8小题)
11. 3≤y≤11 . 12. m<1且m≠0 . 13. ﹣1 .
14. y=﹣x2﹣2x﹣2 . 15. 1 . 16. 2020 .
17. x<﹣3或x>1 . 18. y=﹣(x﹣20)2+16 .
三.解答题(共5小题)
19.二次函数y=x2﹣2x﹣8.
(1)将y=x2﹣2x﹣8用配方法化成y=a(x﹣h)2+k的形式,并写出顶点坐标;
(2)求此函数图象与x轴、y轴的交点坐标.
【解】:(1)∵y=x2﹣2x﹣8=x2﹣2x+1﹣9=(x﹣1)2+9,
∴二次函数图象的顶点坐标为(1,9).
(2)当x=0时,y=x2﹣2x﹣8=﹣8,
∴此函数图象与y轴的交点坐标为(0,﹣8);
当y=0时,x2﹣2x﹣8=0,
解得:x1=﹣2,x2=4,
∴此函数图象与x轴的交点坐标为(﹣2,0)和(4,0).
20.用长为6米的铝合金条制成如图所示的窗框,若窗框的高为x米,窗户的透光面积为S平方米(铝合金条的宽度不计).
(1)S与x之间的函数关系式为 S=﹣x2+3x ,
自变量x的取值范围为 0<x<2 ;
(2)如何安排窗框的高和宽,才能使窗户的透光面积最大?最大面积是多少?
【解】:(1)根据题意,得
窗框的高为x米,则长为(6﹣3x),
所以S=(6﹣3x)?x=﹣x2+3x.
因为x>0,6﹣3x>0,
所以0<x<2.
故答案为S=﹣x2+3x、0<x<2.
(2)S=﹣x2+3x=﹣(x﹣1)2+
∵﹣<0,
∴当x=1时,S有最大值,
即窗框的高为1米,宽为1.5米,才能使窗户的透光面积最大,最大面积是1.5平方米.
答:窗框的高为1米,宽为1.5米,才能使窗户的透光面积最大,最大面积是1.5平方米.
21.如图,二次函数y=(x﹣3)2+m的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点,已知一次函数y=kx+b的图象经过该二次函数图象上的点A(1,0)及点B.
(1)求二次函数与一次函数的解析式;
(2)抛物线上是否存在一点P,使S△ABP=S△ABC?若存在,请求出点P的坐标,若不存在,请说明理由.
【解】:(1)将点A(1,0)代入y=(x﹣3)2+m得(1﹣3)2+m=0,
解得m=﹣4.
所以二次函数解析式为y=(x﹣3)2﹣4,
即y=x2﹣6x+5;
当x=0时,y=9﹣4=5,
所以C点坐标为(0,5),
由于C和B关于对称轴对称,而抛物线的对称轴为直线x=3,
所以B点坐标为(6,5),
将A(1,0)、B(6,5)代入y=kx+b得,
, 解得:.
所以一次函数解析式为y=x﹣1;
(2)假设存在点P,设点P(a,a2﹣6a+5),
∵S△ABP=S△ABC,
∵,
如图1,当点P在直线AB的下方时,过点P作PE∥y轴交直线AB于点E,
∴,
∴E(a,a﹣1)
∴PE=﹣a2+7a﹣6,
∴,
∴a2﹣7a+12=0
解得:a1=4,a2=3,
∴P1(3,﹣4),P2(4,﹣3),
如图2,当点P在直线AB的上方时,过点P作PF∥y轴交直线AB于F,
同理可得=15,
∴,
解得a=0(舍去),a=7,
∴P3(7,12).
综合以上可得P点坐标为(3,﹣4)或(4,﹣3或)(7,12).
22.在平面直角坐标系中,抛物线y=mx2﹣2x+n与x轴的两个交点分别为A(﹣3,0),B(1,0),C为顶点.
(1)求m、n的值.
(2)在y轴上是否存在点D,使得△ACD是以AC为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由.
【解】:(1)把A(﹣3,0),B(1,0)代入y=mx2﹣2x+n得,,
解得:;
故m的值为﹣1,n的值为3;
(2)存在,
理由:过C作CE⊥y轴于E,
∵抛物线的解析式为y=﹣x2﹣2x+3,
∴y=﹣(x+1)2+4,
∴C(﹣1,4),
∴CE=1,OE=4,
设D(0,a),
则OD=a,DE=4﹣a,
∵△ACD是以AC为斜边的直角三角形,
∴∠CDE+∠ADO=90°,
∴∠CDE=∠DAO,
∴△CDE∽△DAO,
∴=,
∴=,
∴a1=1,a2=3,
∴点D的坐标为(0,1)或(0,3).
23.小哲的姑妈经营一家花店,随着越来越多的人喜爱“多肉植物”,姑妈也打算销售“多肉植物”、小哲帮助姑妈针对某种“多肉植物”做了市场调查后,绘制了以下两张图表:
(1)如果在三月份出售这种植物,单株获利 1 元;
(2)单株售价y1与月份x之间的关系式为 y1=﹣x+7 ;单株成本y2与月份x之间的关系式为 y2=(x﹣6)2+1 ;
(3)请你运用所学知识,帮助姑妈求出在哪个月销售这种多肉植物,单株获利最大(提示:单株获利=单株售价﹣单株成本).
【解】:(1)从左图看,3月份售价为5元,从右图看,3月份的成本为4元,
则每株获利为5﹣4=1(元),
故答案为:1;
(2)设直线的表达式为:y1=kx+b(k≠0),
把点(3,5)、(6,3)代入上式得:
,解得:,
∴直线的表达式为:y1=﹣x+7;
设:抛物线的表达式为:y2=a(x﹣m)2+n,
∵顶点为(6,1),则函数表达式为:y2=a(x﹣6)2+1,
把点(3,4)代入上式得:
4=a(3﹣6)2+1,解得:a=,
则抛物线的表达式为:y2=(x﹣6)2+1,
故答案为:y1=﹣x+7;y2=(x﹣6)2+1,
(3)y1﹣y2=﹣x+7﹣(x﹣6)2﹣1=﹣(x﹣5)2+,
∵a=﹣<0,
∴x=5时,函数取得最大值,
故:5月销售这种多肉植物,单株获利最大.
第4题图
第2题图
第9题图
第18题图
第17题图
