人教版物理选修3-1第一章 静电场7 静电现象的应用 共22张PPT
文档属性
| 名称 | 人教版物理选修3-1第一章 静电场7 静电现象的应用 共22张PPT |
|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2019-12-07 18:04:18 | ||
图片预览





文档简介
(共22张PPT)
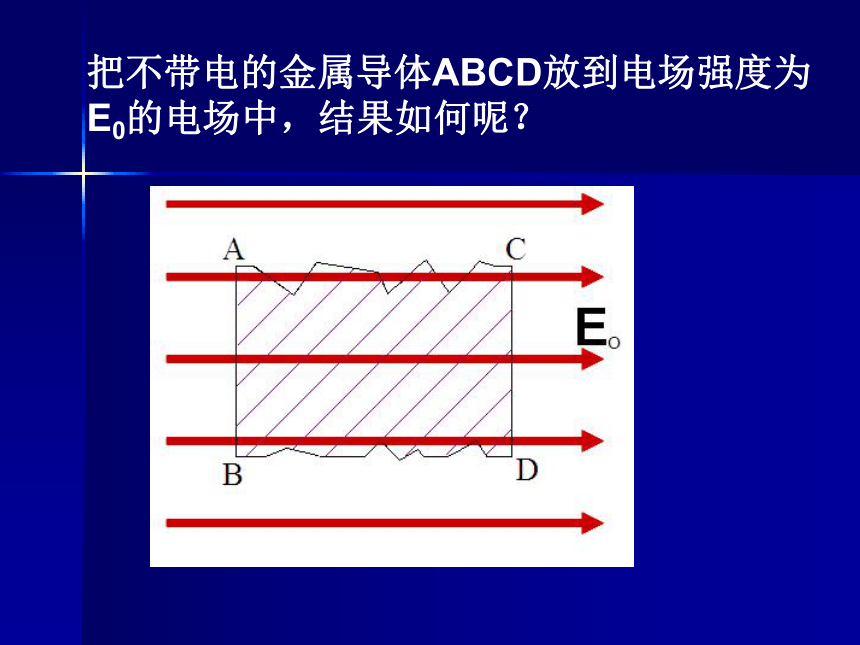
1、什么是静电感应现象?静电感应的实质是什么?
2、是什么力使导体中的正负电荷分开,电荷重新分布稳定后,导体表面和内部有电荷移动吗?
电荷在物体内部转移
静电力; 没有
7.静电现象的应用
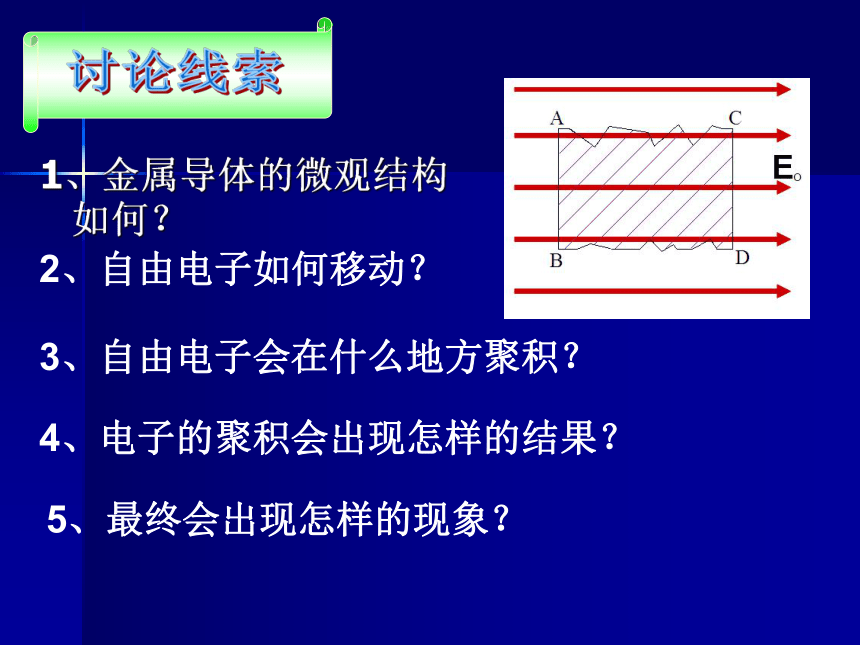
把不带电的金属导体ABCD放到电场强度为E0的电场中,结果如何呢?
1、金属导体的微观结构如何?
2、自由电子如何移动?
3、自由电子会在什么地方聚积?
4、电子的聚积会出现怎样的结果?
5、最终会出现怎样的现象?
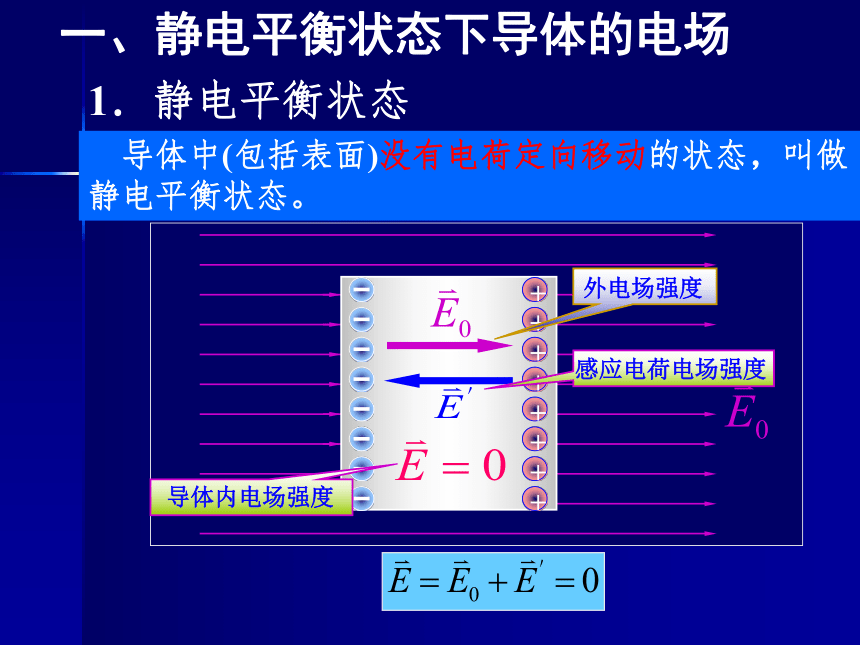
一、静电平衡状态下导体的电场
1.静电平衡状态
导体中(包括表面)没有电荷定向移动的状态,叫做静电平衡状态。
(1)静电平衡状态导体的特点
①处于静电平衡状态的导体,内部场强处处为零。
②处于静电平衡状态的导体,其外部表面附近任何一点的场强方向必跟该点的表面垂直。
③处于静电平衡状态的整个导体是个等势体,它的表面是个等势面。
地球是个大等势体,常被选为零势面
思考① :导体处于静电平衡状态时,为什么内部场强处处为零?
如果静电平衡时导体内部的电场不为0,那么自由电子就会在库仑力的作用下做定向移动,那就不是静电平衡状态了。
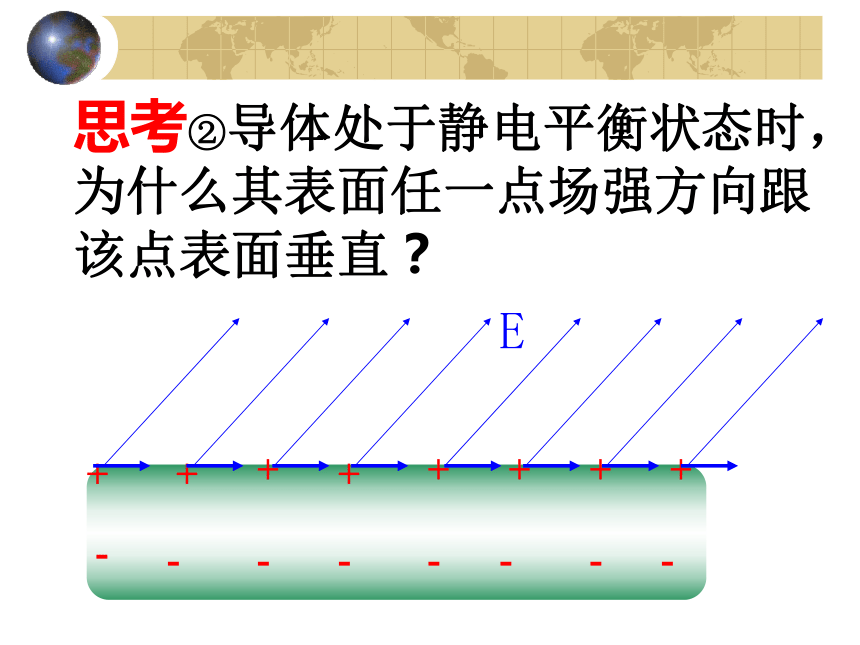
思考②导体处于静电平衡状态时,为什么其表面任一点场强方向跟该点表面垂直?
思考③ :导体处于静电平衡状态时,为什么整个导体是个等势体,它的表面是个等势面?
如果静电平衡时导体不是等势体,那么自由电子就要向电势高的方向做定向移动,那么就不是静电平衡状态了。
二、导体上电荷的分布
研究静电平衡时导体内部的电荷
现象:
甲:A的箔片张角逐渐增大
乙:A的箔片始终没有张开
结论:
导体内部没有电荷,电荷分布在导体的外表面
导体表面越尖锐的位置电荷越密集,凹陷的位置几乎没有电荷
——法拉第圆筒
实验
导体尖端电荷密度大
尖端周围电场强
空气中残留带电粒子剧烈运动
空气电离
正负电荷奔向异种电荷
尖端失去电荷
尖端放电
应用:
避雷针
三、尖端放电
带电云层接近建筑物
避雷针感应出相反电荷
不断向大气释放
中和空气中的电荷
使建筑物避免雷击
尖端放电的应用 :避雷针,静电除尘器,电子打火,高压设备表面制作较为平滑的原因等。
四、静电屏蔽
张开
不张开
四、静电屏蔽
1、概念:由于金属网罩或金属壳内的电场强度保持为0,遮挡了外界电场对金属网罩或金属壳内部的影响,这种现象叫静电屏蔽。
2、静电屏蔽两种情况
(1)空腔导体或金属网罩(无论接地与否)可以把外部电场遮住,使壳内不受外电场影响;
(2)接地空腔导体或金属网罩内部电场对壳外空间没有影响。
3、静电屏蔽的应用:电子仪器外套金属网罩;通讯电缆外包一层铅皮高压作业服等。
1.静电平衡状态下导体的电场
学习了静电平衡、静电平衡状态的概念,知道静电平衡的条件是导体内部的场强处处为零。学习了静电平衡导体的特点
2.导体上电荷的分布
(1)导体内部没有电荷,电荷只分布在导体的外表面。
(2)在导体表面,越尖锐的位置,电荷的密度越大。
3.尖端放电
了解了尖端放电现象及其应用。
4.静电屏蔽
了解了静电屏蔽现象及其应用。
课堂小结
1.关于静电平衡,下列说法中正确的是( )
A.当导体达到静电平衡时,导体上任意两点间的电势一定相等
B.当导体达到静电平衡时,其外表面附近的电场方向一定与导体的表面垂直
C.绝缘体也有静电平衡状态
D.达到静电平衡时,电荷分布在导体的外表面
ABD
检测反馈
2、如图,为一空腔球形导体(不带电)现将
一个带正电的小球A放入腔中,当静电平衡
时,图中a,b,c三点的场强大小关系是( )
A.Ea>Eb>Ec
B. Ea=Eb>Ec
C. Ea=Eb=Ec
D. Ea>Ec> Eb
D
b
c
a
思考:abc三点电势有什么关系?
检测反馈
3、长为L的导体棒原来不带电,现将一电荷量为+q的点电荷放在与棒的左端距离为R的地方,如图所示。达到静电平衡后,棒上的感应电荷在棒内中点O处产生的场强有多大?方向如何?
检测反馈
4.关于避雷针,以下说法正确的是( )
A. 避雷针避雷是中和云层的异种电荷
B. 避雷针避雷是将云层中积聚的电荷导入大地
C. 为了美观,通常把避雷针顶端设计成球形
D. 避雷针安装在高大建筑物顶部,而不必接地
A
检测反馈
5.一个不带电的空心金属球,在它的球心处放一个正点荷。图中的哪一个能正确表示其电场分布的情况 ( )
B
D
7.在一个导体球壳内放一个电量为+Q的点电荷,用E表示球壳外任一点的场强,则( )
A.当+Q在球壳中央时,E=0
B.不论+Q在球壳内何处,E一定为零
C.只有当+Q在球心且球壳接地时,
E=0
D.只要球壳接地,不论+Q在球壳内何处,E一定为零
D
1、什么是静电感应现象?静电感应的实质是什么?
2、是什么力使导体中的正负电荷分开,电荷重新分布稳定后,导体表面和内部有电荷移动吗?
电荷在物体内部转移
静电力; 没有
7.静电现象的应用
把不带电的金属导体ABCD放到电场强度为E0的电场中,结果如何呢?
1、金属导体的微观结构如何?
2、自由电子如何移动?
3、自由电子会在什么地方聚积?
4、电子的聚积会出现怎样的结果?
5、最终会出现怎样的现象?
一、静电平衡状态下导体的电场
1.静电平衡状态
导体中(包括表面)没有电荷定向移动的状态,叫做静电平衡状态。
(1)静电平衡状态导体的特点
①处于静电平衡状态的导体,内部场强处处为零。
②处于静电平衡状态的导体,其外部表面附近任何一点的场强方向必跟该点的表面垂直。
③处于静电平衡状态的整个导体是个等势体,它的表面是个等势面。
地球是个大等势体,常被选为零势面
思考① :导体处于静电平衡状态时,为什么内部场强处处为零?
如果静电平衡时导体内部的电场不为0,那么自由电子就会在库仑力的作用下做定向移动,那就不是静电平衡状态了。
思考②导体处于静电平衡状态时,为什么其表面任一点场强方向跟该点表面垂直?
思考③ :导体处于静电平衡状态时,为什么整个导体是个等势体,它的表面是个等势面?
如果静电平衡时导体不是等势体,那么自由电子就要向电势高的方向做定向移动,那么就不是静电平衡状态了。
二、导体上电荷的分布
研究静电平衡时导体内部的电荷
现象:
甲:A的箔片张角逐渐增大
乙:A的箔片始终没有张开
结论:
导体内部没有电荷,电荷分布在导体的外表面
导体表面越尖锐的位置电荷越密集,凹陷的位置几乎没有电荷
——法拉第圆筒
实验
导体尖端电荷密度大
尖端周围电场强
空气中残留带电粒子剧烈运动
空气电离
正负电荷奔向异种电荷
尖端失去电荷
尖端放电
应用:
避雷针
三、尖端放电
带电云层接近建筑物
避雷针感应出相反电荷
不断向大气释放
中和空气中的电荷
使建筑物避免雷击
尖端放电的应用 :避雷针,静电除尘器,电子打火,高压设备表面制作较为平滑的原因等。
四、静电屏蔽
张开
不张开
四、静电屏蔽
1、概念:由于金属网罩或金属壳内的电场强度保持为0,遮挡了外界电场对金属网罩或金属壳内部的影响,这种现象叫静电屏蔽。
2、静电屏蔽两种情况
(1)空腔导体或金属网罩(无论接地与否)可以把外部电场遮住,使壳内不受外电场影响;
(2)接地空腔导体或金属网罩内部电场对壳外空间没有影响。
3、静电屏蔽的应用:电子仪器外套金属网罩;通讯电缆外包一层铅皮高压作业服等。
1.静电平衡状态下导体的电场
学习了静电平衡、静电平衡状态的概念,知道静电平衡的条件是导体内部的场强处处为零。学习了静电平衡导体的特点
2.导体上电荷的分布
(1)导体内部没有电荷,电荷只分布在导体的外表面。
(2)在导体表面,越尖锐的位置,电荷的密度越大。
3.尖端放电
了解了尖端放电现象及其应用。
4.静电屏蔽
了解了静电屏蔽现象及其应用。
课堂小结
1.关于静电平衡,下列说法中正确的是( )
A.当导体达到静电平衡时,导体上任意两点间的电势一定相等
B.当导体达到静电平衡时,其外表面附近的电场方向一定与导体的表面垂直
C.绝缘体也有静电平衡状态
D.达到静电平衡时,电荷分布在导体的外表面
ABD
检测反馈
2、如图,为一空腔球形导体(不带电)现将
一个带正电的小球A放入腔中,当静电平衡
时,图中a,b,c三点的场强大小关系是( )
A.Ea>Eb>Ec
B. Ea=Eb>Ec
C. Ea=Eb=Ec
D. Ea>Ec> Eb
D
b
c
a
思考:abc三点电势有什么关系?
检测反馈
3、长为L的导体棒原来不带电,现将一电荷量为+q的点电荷放在与棒的左端距离为R的地方,如图所示。达到静电平衡后,棒上的感应电荷在棒内中点O处产生的场强有多大?方向如何?
检测反馈
4.关于避雷针,以下说法正确的是( )
A. 避雷针避雷是中和云层的异种电荷
B. 避雷针避雷是将云层中积聚的电荷导入大地
C. 为了美观,通常把避雷针顶端设计成球形
D. 避雷针安装在高大建筑物顶部,而不必接地
A
检测反馈
5.一个不带电的空心金属球,在它的球心处放一个正点荷。图中的哪一个能正确表示其电场分布的情况 ( )
B
D
7.在一个导体球壳内放一个电量为+Q的点电荷,用E表示球壳外任一点的场强,则( )
A.当+Q在球壳中央时,E=0
B.不论+Q在球壳内何处,E一定为零
C.只有当+Q在球心且球壳接地时,
E=0
D.只要球壳接地,不论+Q在球壳内何处,E一定为零
D
