人教A版数学必修1第一章 集合与函数概念1.3 函数的基本性质 (课件)
文档属性
| 名称 | 人教A版数学必修1第一章 集合与函数概念1.3 函数的基本性质 (课件) |  | |
| 格式 | zip | ||
| 文件大小 | 973.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-11 11:49:39 | ||
图片预览







文档简介
(共33张PPT)
1、掌握一次函数和反比例函数的值域;
2、掌握二次函数在闭区间上的最值问题;
3、学会处理含参数的二次函数的最值问题。
一、求定义域;
求函数的值域:
二、结合函数解析式,采取适当的方法,求值域;
函数的值域:
函数值y的取值范围.
例1:求下列函数的值域
解:(1)
值域是[-1,5]
∴y≠1
即函数的值域是 { y| y?1}
三、不同函数的值域:
(1) 一次函数:y=kx+b(k≠0)
当k>0时,x越大, y越大;
当k=0时,y=b,值域为{b};
当k<0时,x越大, y越小。
值域为{y|y ≠0}
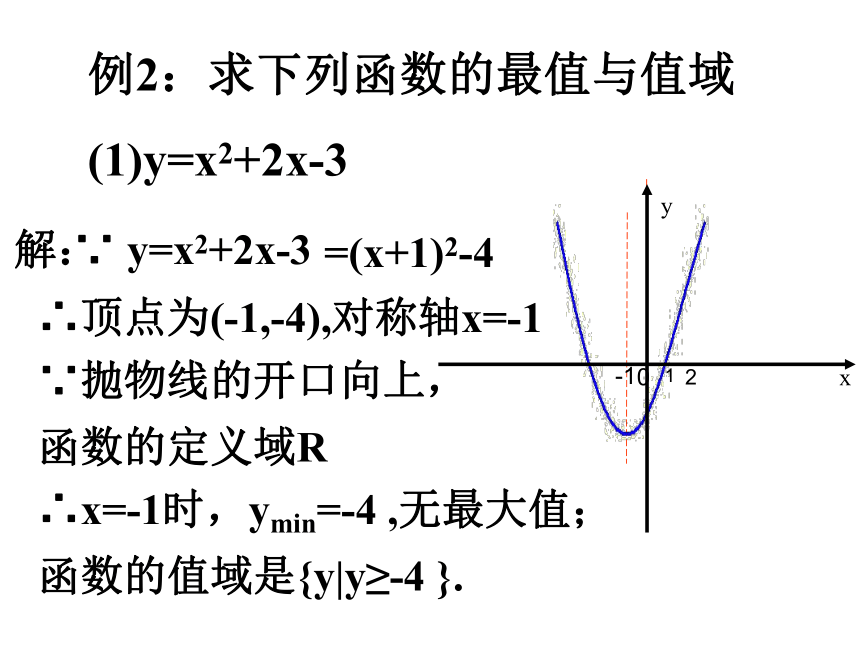
(1)y=x2+2x-3
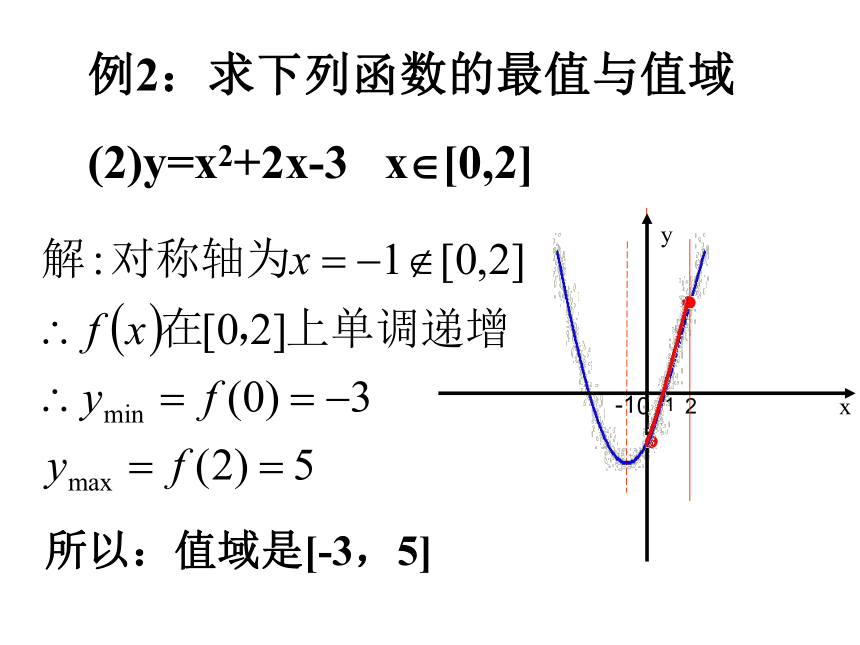
(2)y=x2+2x-3 x?[0,2]
(3)y=x2+2x-3 , x?[-3,-2]
(4)y=x2+2x-3 x?[-2,2]
例2:求下列函数的最值与值域
例2:求下列函数的最值与值域
(1)y=x2+2x-3
∵ y=x2+2x-3
=(x+1)2-4
∴顶点为(-1,-4),对称轴x=-1
∵抛物线的开口向上,
函数的定义域R
∴x=-1时,ymin=-4 ,无最大值;
函数的值域是{y|y≥-4 }.
解:
(2)y=x2+2x-3 x?[0,2]
例2:求下列函数的最值与值域
所以:值域是[-3,5]
(3)y=x2+2x-3 , x?[-3,-2]
例2:求下列函数的最值与值域
所以:值域是[-3,0]
(4)y=x2+2x-3 x?[-2,2]
例2:求下列函数的最值与值域
所以:值域是[-4,5]
总结:要求最值,就要考察函数在区间上
是否具有单调性,对于二次函数就
要考察函数图象的对称轴与区间的
位置关系。
问题2
问题3
问题4
二次函数 y= ax2+bx+c 在区间 [m,n]上的最值问题,一般情况下,按对称轴与区间的关系分三种情况讨论求解.
x=a
对称轴 x=a,
对称轴 x=a,
对称轴 x=a,
对称轴 x=a,
评注:此题属于“轴动区间定”的问题,看作对称轴沿x轴移动的过程中,函数最值的变化,实质是讨论对称轴与区间的两个端点及两端点中点的位置关系,即对称轴在定区间的左、右两侧及对称轴在定区间上变化情况,要注意开口方向及端点情况。
例4:二次函数f(x)=x2-2x-3在[-3,a] (a>-3)上的最值是多少?
fmin=f(a)=a2-2a-3
fmax=f(-3)=12
fmin=f(1)=-4
fmax=f(-3)=12
例4:二次函数f(x)=x2-2x-3在[-3,a] (a>-3)上的最值是多少?
fmin=f(1)=-4
fmax=f(a)= a2-2a-3
例4:二次函数f(x)=x2-2x-3在[-3,a] (a>-3)上的最值是多少?
评注:此题属于“轴定区间动”的问题,看作区间沿x轴移动的过程中,函数最值的变化,实质是讨论对称轴与区间的两个端点的位置关系。
例4:二次函数f(x)=x2-2x-3在[-3,a] (a>-3)上的最值是多少?
三、不同函数的值域:
(4) 分段函数:
分段函数的定义域是各段定义域的
并集,值域是各段值域的并集。
解:定义域为R
∴值域是{y|y≥3 }.
练习:求函数y = | x + 1 | -| x - 1 |的值域
解:由y = | x + 1 | -| x -1 |
当 x ≤- 1 时,
y = -( x + 1 ) + ( x -1 ) = -2
当 -1 < x ≤ 1 时,
y = ( x + 1 ) + ( x -1 ) = 2x
当 x > 1 时,
y = ( x + 1 ) - ( x -1 ) = 2
由图知: -2 ≤ y ≤ 2
故函数的值域为
[-2 , 3 ]
练习:求函数y = | x + 1 | -| x - 1 |的值域
则x=1-t2且t≥0
y=1-t2+t
例6:求下列函数的值域
换元法
1、掌握一次函数和反比例函数的值域;
2、掌握二次函数在闭区间上的最值问题;
3、学会处理含参数的二次函数的最值问题。
一、求定义域;
求函数的值域:
二、结合函数解析式,采取适当的方法,求值域;
函数的值域:
函数值y的取值范围.
例1:求下列函数的值域
解:(1)
值域是[-1,5]
∴y≠1
即函数的值域是 { y| y?1}
三、不同函数的值域:
(1) 一次函数:y=kx+b(k≠0)
当k>0时,x越大, y越大;
当k=0时,y=b,值域为{b};
当k<0时,x越大, y越小。
值域为{y|y ≠0}
(1)y=x2+2x-3
(2)y=x2+2x-3 x?[0,2]
(3)y=x2+2x-3 , x?[-3,-2]
(4)y=x2+2x-3 x?[-2,2]
例2:求下列函数的最值与值域
例2:求下列函数的最值与值域
(1)y=x2+2x-3
∵ y=x2+2x-3
=(x+1)2-4
∴顶点为(-1,-4),对称轴x=-1
∵抛物线的开口向上,
函数的定义域R
∴x=-1时,ymin=-4 ,无最大值;
函数的值域是{y|y≥-4 }.
解:
(2)y=x2+2x-3 x?[0,2]
例2:求下列函数的最值与值域
所以:值域是[-3,5]
(3)y=x2+2x-3 , x?[-3,-2]
例2:求下列函数的最值与值域
所以:值域是[-3,0]
(4)y=x2+2x-3 x?[-2,2]
例2:求下列函数的最值与值域
所以:值域是[-4,5]
总结:要求最值,就要考察函数在区间上
是否具有单调性,对于二次函数就
要考察函数图象的对称轴与区间的
位置关系。
问题2
问题3
问题4
二次函数 y= ax2+bx+c 在区间 [m,n]上的最值问题,一般情况下,按对称轴与区间的关系分三种情况讨论求解.
x=a
对称轴 x=a,
对称轴 x=a,
对称轴 x=a,
对称轴 x=a,
评注:此题属于“轴动区间定”的问题,看作对称轴沿x轴移动的过程中,函数最值的变化,实质是讨论对称轴与区间的两个端点及两端点中点的位置关系,即对称轴在定区间的左、右两侧及对称轴在定区间上变化情况,要注意开口方向及端点情况。
例4:二次函数f(x)=x2-2x-3在[-3,a] (a>-3)上的最值是多少?
fmin=f(a)=a2-2a-3
fmax=f(-3)=12
fmin=f(1)=-4
fmax=f(-3)=12
例4:二次函数f(x)=x2-2x-3在[-3,a] (a>-3)上的最值是多少?
fmin=f(1)=-4
fmax=f(a)= a2-2a-3
例4:二次函数f(x)=x2-2x-3在[-3,a] (a>-3)上的最值是多少?
评注:此题属于“轴定区间动”的问题,看作区间沿x轴移动的过程中,函数最值的变化,实质是讨论对称轴与区间的两个端点的位置关系。
例4:二次函数f(x)=x2-2x-3在[-3,a] (a>-3)上的最值是多少?
三、不同函数的值域:
(4) 分段函数:
分段函数的定义域是各段定义域的
并集,值域是各段值域的并集。
解:定义域为R
∴值域是{y|y≥3 }.
练习:求函数y = | x + 1 | -| x - 1 |的值域
解:由y = | x + 1 | -| x -1 |
当 x ≤- 1 时,
y = -( x + 1 ) + ( x -1 ) = -2
当 -1 < x ≤ 1 时,
y = ( x + 1 ) + ( x -1 ) = 2x
当 x > 1 时,
y = ( x + 1 ) - ( x -1 ) = 2
由图知: -2 ≤ y ≤ 2
故函数的值域为
[-2 , 3 ]
练习:求函数y = | x + 1 | -| x - 1 |的值域
则x=1-t2且t≥0
y=1-t2+t
例6:求下列函数的值域
换元法
