15.2 线段的垂直平分线学案(要点讲解+当堂检测+答案)
文档属性
| 名称 | 15.2 线段的垂直平分线学案(要点讲解+当堂检测+答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-06 00:00:00 | ||
图片预览

文档简介
沪科版数学八年级上册同步学案
第15章 轴对称图形与等腰三角形
15.2 线段的垂直平分线
要 点 讲 解
要点一 线段垂直平分线的作法
利用尺规作图法作出线段的垂直平分线.
根据两点确定一条直线,只要找出到这条线段的两个端点距离相等的两个点,过这两个点作直线就能得到这条线段的垂直平分线.
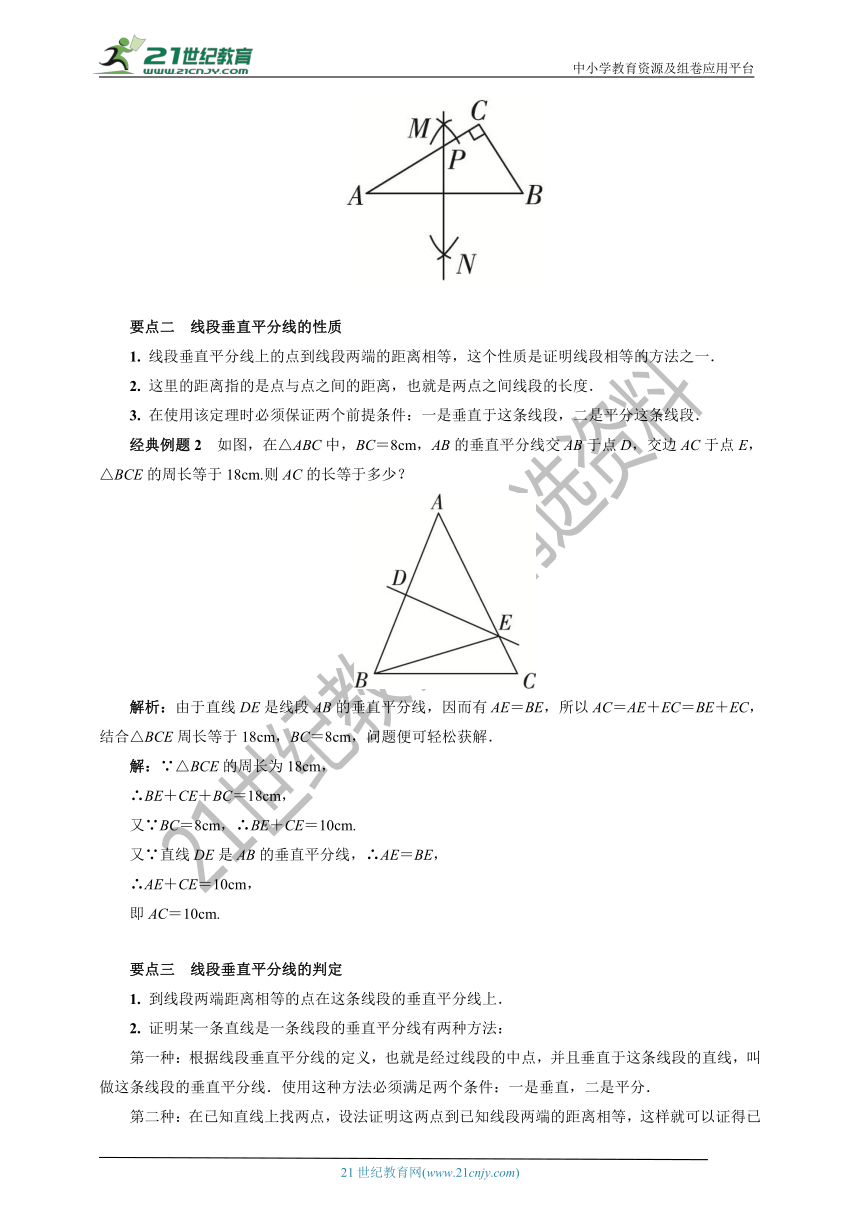
已知:线段AB,如图所示.
求作:线段AB的垂直平分线.
作法:(1)分别以点A和点B为圆心,以大于AB的长为半径作弧,两弧相交于点C和点D.
(2)过C,D两点作直线CD,则直线CD即为线段AB的垂直平分线.
经典例题1 如图,在△ABC中,∠C=90°,用直尺和圆规在AC上作点P,使P到A,B的距离相等(保留作图痕迹).
解析:P到A,B的距离相等,说明P在线段AB的垂直平分线上,也就意味着这一点是线段AB的垂直平分线与AC的交点.
解:如图所示.分别以A,B为圆心,大于AB的长为半径作弧分别交于M,N两点,过M,N作直线交AC于点P,则点P即为所求作的点.
要点二 线段垂直平分线的性质
1. 线段垂直平分线上的点到线段两端的距离相等,这个性质是证明线段相等的方法之一.
2. 这里的距离指的是点与点之间的距离,也就是两点之间线段的长度.
3. 在使用该定理时必须保证两个前提条件:一是垂直于这条线段,二是平分这条线段.
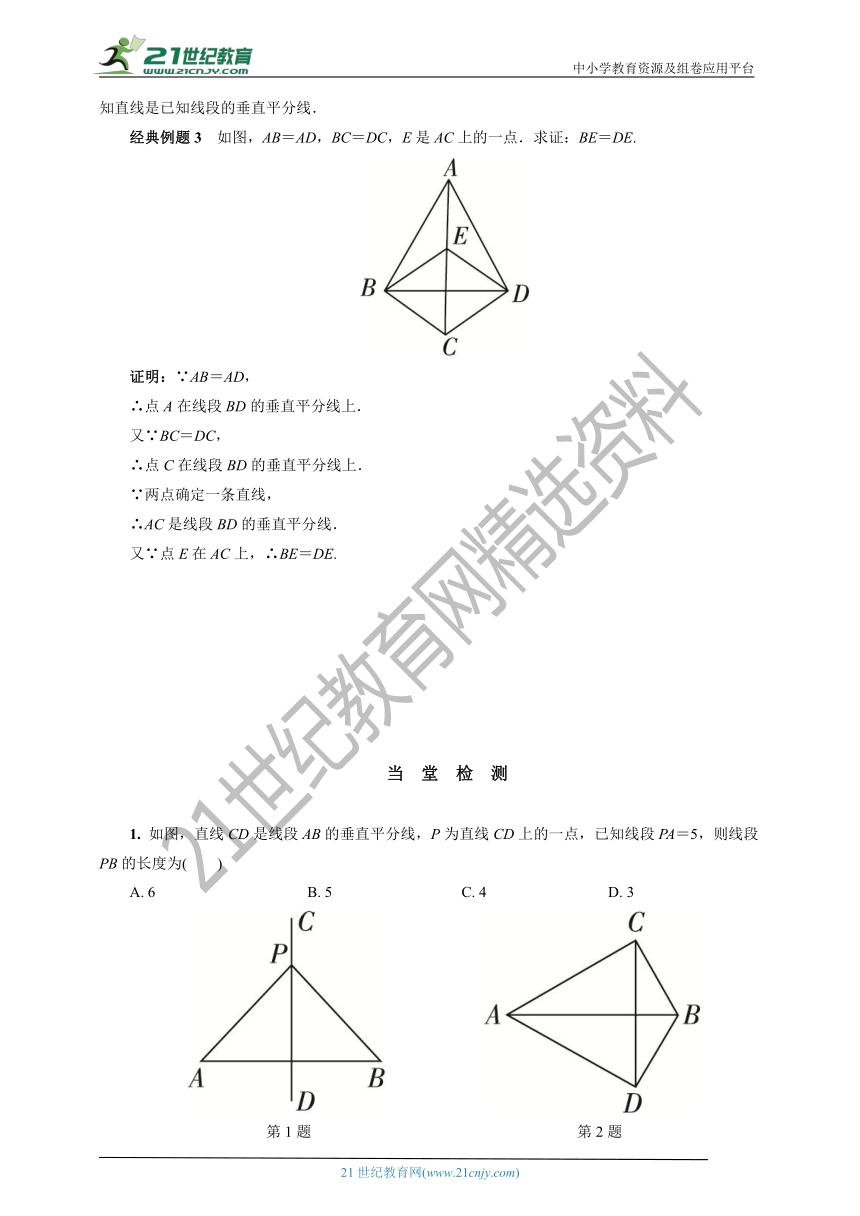
经典例题2 如图,在△ABC中,BC=8cm,AB的垂直平分线交AB于点D,交边AC于点E,△BCE的周长等于18cm.则AC的长等于多少?
解析:由于直线DE是线段AB的垂直平分线,因而有AE=BE,所以AC=AE+EC=BE+EC,结合△BCE周长等于18cm,BC=8cm,问题便可轻松获解.
解:∵△BCE的周长为18cm,
∴BE+CE+BC=18cm,
又∵BC=8cm,∴BE+CE=10cm.
又∵直线DE是AB的垂直平分线,∴AE=BE,
∴AE+CE=10cm,
即AC=10cm.
要点三 线段垂直平分线的判定
1. 到线段两端距离相等的点在这条线段的垂直平分线上.
2. 证明某一条直线是一条线段的垂直平分线有两种方法:
第一种:根据线段垂直平分线的定义,也就是经过线段的中点,并且垂直于这条线段的直线,叫做这条线段的垂直平分线.使用这种方法必须满足两个条件:一是垂直,二是平分.
第二种:在已知直线上找两点,设法证明这两点到已知线段两端的距离相等,这样就可以证得已知直线是已知线段的垂直平分线.
经典例题3 如图,AB=AD,BC=DC,E是AC上的一点.求证:BE=DE.
证明:∵AB=AD,
∴点A在线段BD的垂直平分线上.
又∵BC=DC,
∴点C在线段BD的垂直平分线上.
∵两点确定一条直线,
∴AC是线段BD的垂直平分线.
又∵点E在AC上,∴BE=DE.
当 堂 检 测
1. 如图,直线CD是线段AB的垂直平分线,P为直线CD上的一点,已知线段PA=5,则线段PB的长度为( )
A. 6 B. 5 C. 4 D. 3
第1题 第2题
2. 如图,AB是CD的垂直平分线,若BD=1.6cm,AC=2.3cm,则四边形ACBD的周长是( )
A. 3.9cm B. 7.8cm C. 4cm D. 4.6cm
3. 如图,CD是线段AB的垂直平分线,垂足为D,下列结论:①AD=BD;②AC=BC;③∠A=∠B;④∠ACD=∠BCD;⑤∠ADC=∠BDC=90°.其中正确的有( )
A. 2个 B. 3个 C. 4个 D. 5个
第3题 第4题
4. 如图,已知OC=OD,则下列说法不正确的是( )
A. OP=DP B. CA=DA
C. OP⊥CD D. 点O在CD的垂直平分线上
5. 如图,在△ABC中,DE垂直平分AC交AB于点E,∠A=30°,∠ACB=80°,则∠BCE= .
第5题 第6题
6. 如图,在△ABC中,直线DE是AC的垂直平分线,AE=5cm,△ABD的周长为13cm,则△ABC的周长= .
7. 如图,点A,点B关于某条直线成轴对称,你能作出这条直线吗?
8. 如图,AD⊥BC,BD=CD,点C在AE的垂直平分线上.若AB=5cm,BD=3cm,求BE的长.
9. 如图,在△ABC中,AB的垂直平分线交BC于点D,交AB于点E,AC的垂直平分线交BC于点F,交AC于点G,△ADF的周长为14.
(1)求BC的长;
(2)若∠B+∠C=70°,求∠DAF的度数.
当堂检测参考答案
1. B 2. B 3. D 4. A
5. 50°
6. 23cm
7. 解:连接AB,作线段AB的垂直平分线,如图所示.
8. 解:∵AD⊥BC,BD=CD,∴AB=AC,∵点C在AE的垂直平分线上,∴AC=CE,∴AB=CD.∵AB=5cm,BD=3cm,∴CE=5cm,CD=3cm.∴BE=BD+DC+CE=11cm.
9. 解:(1)∵DE垂直平分AB,FG垂直平分AC,∴BD=AD,AF=CF,∴BC=BD+DF+FC=AD+DF+AF=14.
(2)∵DE垂直平分AB,FG垂直平分AC,∴△DBE和△DAE关于DE对称,△FGC和△FGA关于FG对称,∴∠B=∠BAD,∠C=∠CAF.∵∠B+∠C=70°,∴∠BAC=180°-70°=110°,∠BAD+∠CAF=70°,∴∠DAF=110°-70°=40°.
第15章 轴对称图形与等腰三角形
15.2 线段的垂直平分线
要 点 讲 解
要点一 线段垂直平分线的作法
利用尺规作图法作出线段的垂直平分线.
根据两点确定一条直线,只要找出到这条线段的两个端点距离相等的两个点,过这两个点作直线就能得到这条线段的垂直平分线.
已知:线段AB,如图所示.
求作:线段AB的垂直平分线.
作法:(1)分别以点A和点B为圆心,以大于AB的长为半径作弧,两弧相交于点C和点D.
(2)过C,D两点作直线CD,则直线CD即为线段AB的垂直平分线.
经典例题1 如图,在△ABC中,∠C=90°,用直尺和圆规在AC上作点P,使P到A,B的距离相等(保留作图痕迹).
解析:P到A,B的距离相等,说明P在线段AB的垂直平分线上,也就意味着这一点是线段AB的垂直平分线与AC的交点.
解:如图所示.分别以A,B为圆心,大于AB的长为半径作弧分别交于M,N两点,过M,N作直线交AC于点P,则点P即为所求作的点.
要点二 线段垂直平分线的性质
1. 线段垂直平分线上的点到线段两端的距离相等,这个性质是证明线段相等的方法之一.
2. 这里的距离指的是点与点之间的距离,也就是两点之间线段的长度.
3. 在使用该定理时必须保证两个前提条件:一是垂直于这条线段,二是平分这条线段.
经典例题2 如图,在△ABC中,BC=8cm,AB的垂直平分线交AB于点D,交边AC于点E,△BCE的周长等于18cm.则AC的长等于多少?
解析:由于直线DE是线段AB的垂直平分线,因而有AE=BE,所以AC=AE+EC=BE+EC,结合△BCE周长等于18cm,BC=8cm,问题便可轻松获解.
解:∵△BCE的周长为18cm,
∴BE+CE+BC=18cm,
又∵BC=8cm,∴BE+CE=10cm.
又∵直线DE是AB的垂直平分线,∴AE=BE,
∴AE+CE=10cm,
即AC=10cm.
要点三 线段垂直平分线的判定
1. 到线段两端距离相等的点在这条线段的垂直平分线上.
2. 证明某一条直线是一条线段的垂直平分线有两种方法:
第一种:根据线段垂直平分线的定义,也就是经过线段的中点,并且垂直于这条线段的直线,叫做这条线段的垂直平分线.使用这种方法必须满足两个条件:一是垂直,二是平分.
第二种:在已知直线上找两点,设法证明这两点到已知线段两端的距离相等,这样就可以证得已知直线是已知线段的垂直平分线.
经典例题3 如图,AB=AD,BC=DC,E是AC上的一点.求证:BE=DE.
证明:∵AB=AD,
∴点A在线段BD的垂直平分线上.
又∵BC=DC,
∴点C在线段BD的垂直平分线上.
∵两点确定一条直线,
∴AC是线段BD的垂直平分线.
又∵点E在AC上,∴BE=DE.
当 堂 检 测
1. 如图,直线CD是线段AB的垂直平分线,P为直线CD上的一点,已知线段PA=5,则线段PB的长度为( )
A. 6 B. 5 C. 4 D. 3
第1题 第2题
2. 如图,AB是CD的垂直平分线,若BD=1.6cm,AC=2.3cm,则四边形ACBD的周长是( )
A. 3.9cm B. 7.8cm C. 4cm D. 4.6cm
3. 如图,CD是线段AB的垂直平分线,垂足为D,下列结论:①AD=BD;②AC=BC;③∠A=∠B;④∠ACD=∠BCD;⑤∠ADC=∠BDC=90°.其中正确的有( )
A. 2个 B. 3个 C. 4个 D. 5个
第3题 第4题
4. 如图,已知OC=OD,则下列说法不正确的是( )
A. OP=DP B. CA=DA
C. OP⊥CD D. 点O在CD的垂直平分线上
5. 如图,在△ABC中,DE垂直平分AC交AB于点E,∠A=30°,∠ACB=80°,则∠BCE= .
第5题 第6题
6. 如图,在△ABC中,直线DE是AC的垂直平分线,AE=5cm,△ABD的周长为13cm,则△ABC的周长= .
7. 如图,点A,点B关于某条直线成轴对称,你能作出这条直线吗?
8. 如图,AD⊥BC,BD=CD,点C在AE的垂直平分线上.若AB=5cm,BD=3cm,求BE的长.
9. 如图,在△ABC中,AB的垂直平分线交BC于点D,交AB于点E,AC的垂直平分线交BC于点F,交AC于点G,△ADF的周长为14.
(1)求BC的长;
(2)若∠B+∠C=70°,求∠DAF的度数.
当堂检测参考答案
1. B 2. B 3. D 4. A
5. 50°
6. 23cm
7. 解:连接AB,作线段AB的垂直平分线,如图所示.
8. 解:∵AD⊥BC,BD=CD,∴AB=AC,∵点C在AE的垂直平分线上,∴AC=CE,∴AB=CD.∵AB=5cm,BD=3cm,∴CE=5cm,CD=3cm.∴BE=BD+DC+CE=11cm.
9. 解:(1)∵DE垂直平分AB,FG垂直平分AC,∴BD=AD,AF=CF,∴BC=BD+DF+FC=AD+DF+AF=14.
(2)∵DE垂直平分AB,FG垂直平分AC,∴△DBE和△DAE关于DE对称,△FGC和△FGA关于FG对称,∴∠B=∠BAD,∠C=∠CAF.∵∠B+∠C=70°,∴∠BAC=180°-70°=110°,∠BAD+∠CAF=70°,∴∠DAF=110°-70°=40°.
