人教A版数学必修1第二章 基本初等函数(1)2.2 对数函数 2.2.2 对数函数及其性质(课件)15张PPT
文档属性
| 名称 | 人教A版数学必修1第二章 基本初等函数(1)2.2 对数函数 2.2.2 对数函数及其性质(课件)15张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 404.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-11 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
1、熟练掌握对数函数的概念、图象、 性质;
2、比较两个对数的大小;
3、解对数型不等式。
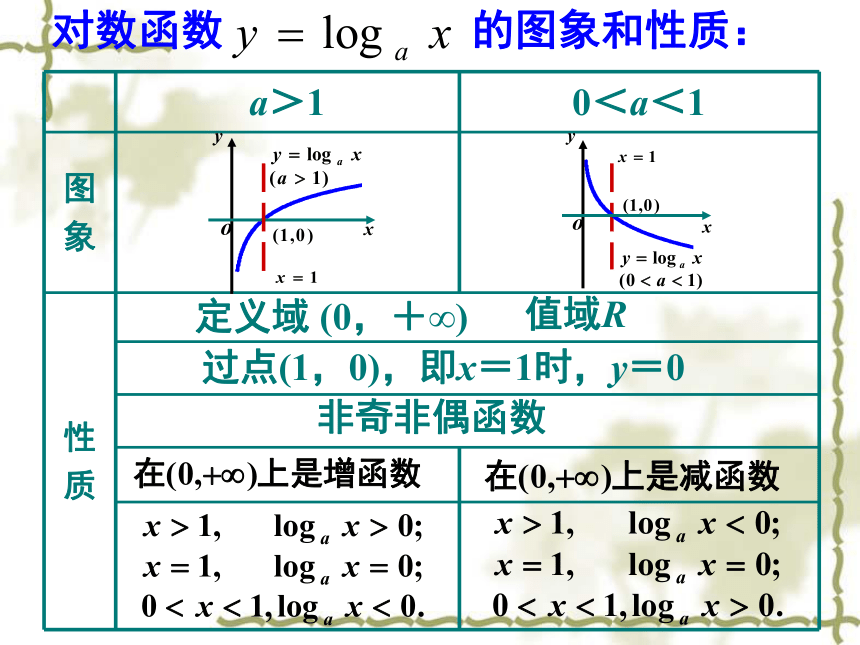
对数函数 的图象和性质:
定义域 (0,+∞)
值域R
过点(1,0),即x=1时,y=0
非奇非偶函数
a>1 0<a<1
图
象
性
质
例1:比较下列各组数中两个值的大小:
(1) log 23.4 , log 28.5
(2) log 0.31.8 , log 0.32.7
(3)log a5.1 , log a5.9 ( a>0 , a≠1 )
所以它在(0,+∞)上是增函数
又因为 3.4 < 8.5
所以 log 23.4<log 28.5
解:(1)考察对数函数 y = log 2x,
解:(2)考察对数函数 y = log 0.3 x,
所以它在(0,+∞)上是减函数,
且1.8<2.7,
故log 0.31.8>log 0.32.7
例1:比较下列各组数中两个值的大小:
(1) log 23.4 , log 28.5
(2) log 0.31.8 , log 0.32.7
(3)log a5.1 , log a5.9 ( a>0 , a≠1 )
解:(3)当a>1时, y=loga x在(0,+∞)上是增函数,
则有loga 5.1<loga 5.9
当0<a<1时, y=loga x在(0,+∞)上是减函数,
则有loga 5.1>loga 5.9
例1:比较下列各组数中两个值的大小:
(1) log 23.4 , log 28.5
(2) log 0.31.8 , log 0.32.7
(3)log a5.1 , log a5.9 ( a>0 , a≠1 )
例1:比较下列各组数中两个值的大小:
(1) log 23.4 , log 28.5
(2) log 0.31.8 , log 0.32.7
(3)log a5.1 , log a5.9 ( a>0 , a≠1 )
方法:
当底数相同,真数不同时,利用对数函数的增减性比较大小。
注意:当底数不确定时,要对底数
与1的大小进行分类讨论。
例2:比较下列各组数中两个值的大小:
解:(1)∵log67>log66=1
log76<log77=1
∴log67>log76
(2)∵log3π>log31=0
log20.8<log21=0
∴log3π>log20.8
当底数不同,真数不同时,
方法:
可考虑这些数与1或0的大小 。
log53 , log43
例3:比较大小:
解:
利用对数函数图象
得到 log53 < log43
y1=log4x
y2=log5x
当底数不同, 真数相同时, 利用图象判断 大小。
方法:
练习2:已知不等式,比较正数m,n的大小:
(1) log 3 m < log 3 n
(2) log 0.3 m > log 0.3 n
练习1:比较下列各组数中两个值的大小:
(1) loga5___ loga3 (a>0,且a≠1);
(2) log87_____log78;
(3) log37_____log27;
>
<
(4) log32,log23, log0.53的大小关系为
___________________________.
log23 > log32 > log0.53
答案:(1) m < n
(2) m < n
例4:解不等式:
解:原不等式可化为:
练习:
1. 函数y=loga(x+1)-2 (a>0, a≠1)
的图象恒过定点 .
解:
(0,-2 )
2. 不等式log2(4x+8)>log22x的解集为( )
A. x>0 B. x> -4 C. x > -2 D. x> 4
A
【总一总★成竹在胸】
2.对数函数的图象和性质;
3.比较两个对数值的大小.
1.对数函数的定义;
1、熟练掌握对数函数的概念、图象、 性质;
2、比较两个对数的大小;
3、解对数型不等式。
对数函数 的图象和性质:
定义域 (0,+∞)
值域R
过点(1,0),即x=1时,y=0
非奇非偶函数
a>1 0<a<1
图
象
性
质
例1:比较下列各组数中两个值的大小:
(1) log 23.4 , log 28.5
(2) log 0.31.8 , log 0.32.7
(3)log a5.1 , log a5.9 ( a>0 , a≠1 )
所以它在(0,+∞)上是增函数
又因为 3.4 < 8.5
所以 log 23.4<log 28.5
解:(1)考察对数函数 y = log 2x,
解:(2)考察对数函数 y = log 0.3 x,
所以它在(0,+∞)上是减函数,
且1.8<2.7,
故log 0.31.8>log 0.32.7
例1:比较下列各组数中两个值的大小:
(1) log 23.4 , log 28.5
(2) log 0.31.8 , log 0.32.7
(3)log a5.1 , log a5.9 ( a>0 , a≠1 )
解:(3)当a>1时, y=loga x在(0,+∞)上是增函数,
则有loga 5.1<loga 5.9
当0<a<1时, y=loga x在(0,+∞)上是减函数,
则有loga 5.1>loga 5.9
例1:比较下列各组数中两个值的大小:
(1) log 23.4 , log 28.5
(2) log 0.31.8 , log 0.32.7
(3)log a5.1 , log a5.9 ( a>0 , a≠1 )
例1:比较下列各组数中两个值的大小:
(1) log 23.4 , log 28.5
(2) log 0.31.8 , log 0.32.7
(3)log a5.1 , log a5.9 ( a>0 , a≠1 )
方法:
当底数相同,真数不同时,利用对数函数的增减性比较大小。
注意:当底数不确定时,要对底数
与1的大小进行分类讨论。
例2:比较下列各组数中两个值的大小:
解:(1)∵log67>log66=1
log76<log77=1
∴log67>log76
(2)∵log3π>log31=0
log20.8<log21=0
∴log3π>log20.8
当底数不同,真数不同时,
方法:
可考虑这些数与1或0的大小 。
log53 , log43
例3:比较大小:
解:
利用对数函数图象
得到 log53 < log43
y1=log4x
y2=log5x
当底数不同, 真数相同时, 利用图象判断 大小。
方法:
练习2:已知不等式,比较正数m,n的大小:
(1) log 3 m < log 3 n
(2) log 0.3 m > log 0.3 n
练习1:比较下列各组数中两个值的大小:
(1) loga5___ loga3 (a>0,且a≠1);
(2) log87_____log78;
(3) log37_____log27;
>
<
(4) log32,log23, log0.53的大小关系为
___________________________.
log23 > log32 > log0.53
答案:(1) m < n
(2) m < n
例4:解不等式:
解:原不等式可化为:
练习:
1. 函数y=loga(x+1)-2 (a>0, a≠1)
的图象恒过定点 .
解:
(0,-2 )
2. 不等式log2(4x+8)>log22x的解集为( )
A. x>0 B. x> -4 C. x > -2 D. x> 4
A
【总一总★成竹在胸】
2.对数函数的图象和性质;
3.比较两个对数值的大小.
1.对数函数的定义;
