15.3.3 含30°角的直角三角形的性质学案(要点讲解+当堂检测+答案)
文档属性
| 名称 | 15.3.3 含30°角的直角三角形的性质学案(要点讲解+当堂检测+答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-07 00:00:00 | ||
图片预览


文档简介
沪科版数学八年级上册同步学案
第15章 轴对称图形与等腰三角形
15.3 等腰三角形
第3课时 含30°角的直角三角形的性质
要 点 讲 解
要点 含30°角的直角三角形的性质及应用
1. 在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
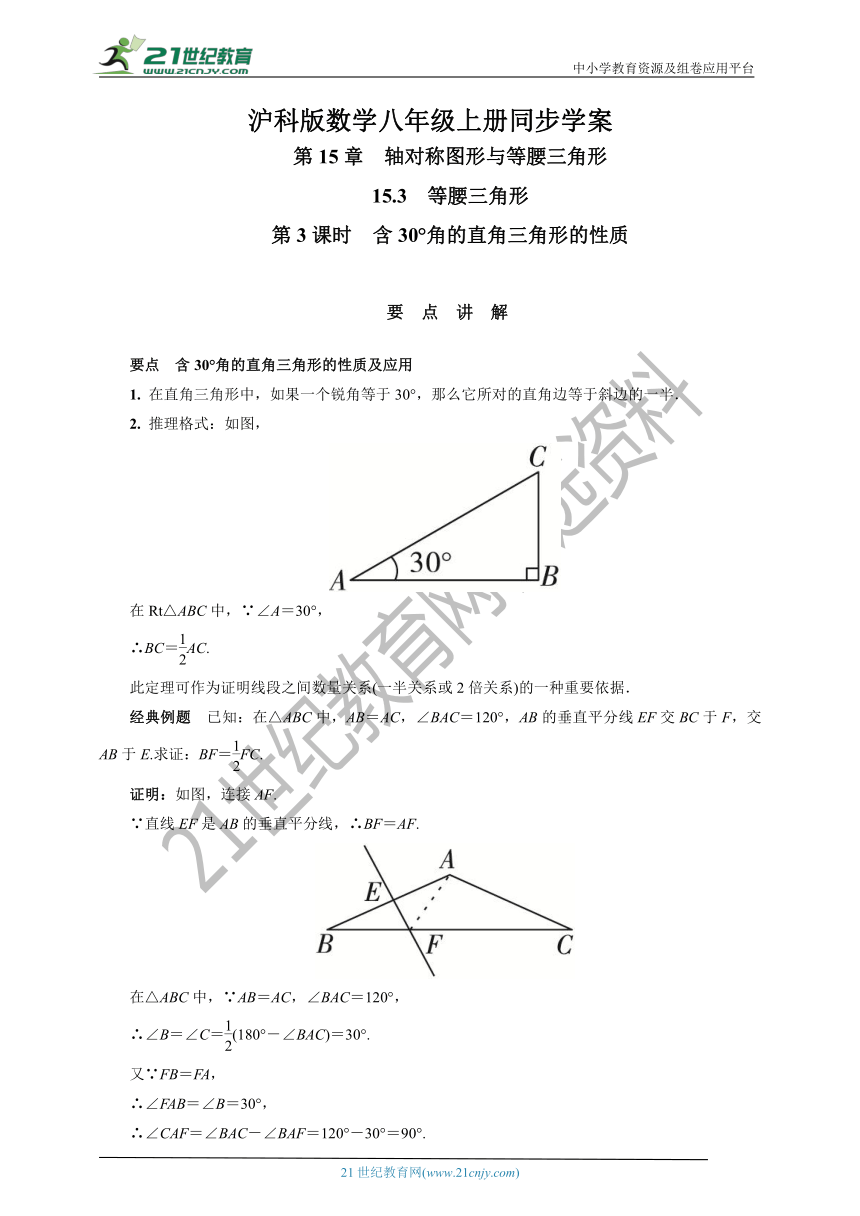
2. 推理格式:如图,
在Rt△ABC中,∵∠A=30°,
∴BC=AC.
此定理可作为证明线段之间数量关系(一半关系或2倍关系)的一种重要依据.
经典例题 已知:在△ABC中,AB=AC,∠BAC=120°,AB的垂直平分线EF交BC于F,交AB于E.求证:BF=FC.
证明:如图,连接AF.
∵直线EF是AB的垂直平分线,∴BF=AF.
在△ABC中,∵AB=AC,∠BAC=120°,
∴∠B=∠C=(180°-∠BAC)=30°.
又∵FB=FA,
∴∠FAB=∠B=30°,
∴∠CAF=∠BAC-∠BAF=120°-30°=90°.
在△ACF中,∠C=30°,∠CAF=90°,
∴AF=FC,
∴BF=FC.
点拨:在利用含30°角的直角三角形的性质时,一定要先证明这个角所在的三角形是直角三角形,此性质是求线段长度和证明线段倍分关系的重要依据.
当 堂 检 测
1. 在直角△ABC中,∠C=30°,斜边AC的长为5cm,则AB的长为( )
A. 4cm B. 3cm C. 2.5cm D. 2cm
2. 如图,折叠直角三角形纸片的直角,使点C落在斜边AB上的点E处,已知CD=1,∠B=30°,则BD的长是( )
A. 1 B. 2 C. D. 2
第2题 第3题
3. 如图,在△ABC中,∠C=90°,∠B=30°,边AB的垂直平分线DE交AB于点E,交BC于点D,CD=3,则BC的长为( )
A. 6 B. 6 C. 9 D. 3
4. 如图是某商场一楼与二楼之间的手扶电梯示意图,其中AB,CD分别表示一楼、二楼地面的水平线,∠ABC=150°,BC的长是8m,则乘电梯从点B到点C上升的高度h是( )
A. 3m B. 4m C. 5m D. 6m
5. 将一副三角尺如图叠放在一起,若AB=10cm,则阴影部分的面积是 cm2.
6. 如图,孔明同学背着一桶水,从山脚A出发,沿与地面30°角的山坡向上走,送水到山上因受旱缺水的王奶奶家(B处),AB=80米,则孔明从A到B上升的高度BC是 米.
7. 如图,一棵树在一次强台风中于离地面4米处折断倒下,倒下部分与地面成30°夹角,这棵树在折断前的高度为 米.
8. 如图,∠C=90°,∠A=30°,BD⊥AD于D,DC∥AB,AB=10,求CD的长.
9. 如图,已知某船于上午8时在A处观测小岛C在北偏东60°方向上,该船以每小时40海里的速度向东航行到B处,此时测得小岛C在北偏东30°方向上.船以原速度继续向东航行2小时到达小岛C的正南方D处,求船从A处到D处一共走了多少海里.
当堂检测参考答案
1. C 2. B 3. C 4. B
5.
6. 40
7. 12
8. 解:在△ABD中,∵BD⊥AD,∠A=30°,∴BD=AB=×10=5,∠ABD=60°.又∵DC∥AB,∴∠CDB=∠DAB=60°.∵∠C=90°,∴∠CBD=30°,∴CD=BD=×5=2.5.
9. 解:由题意知∠CAD=30°,∠CBD=60°,∠CDA=90°,BD=2×40=80(海里).在△BCD中,∠CBD=60°,∴∠BCD=30°,∴BC=2BD=160海里.由∠CBD=60°,得∠ABC=120°,∵∠CAD=30°,∴∠ACB=30°,∴AB=BC=160海里,∵AD=AB+BD,∴AD=160+80=240(海里).即船从A到D一共走了240海里.
第15章 轴对称图形与等腰三角形
15.3 等腰三角形
第3课时 含30°角的直角三角形的性质
要 点 讲 解
要点 含30°角的直角三角形的性质及应用
1. 在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
2. 推理格式:如图,
在Rt△ABC中,∵∠A=30°,
∴BC=AC.
此定理可作为证明线段之间数量关系(一半关系或2倍关系)的一种重要依据.
经典例题 已知:在△ABC中,AB=AC,∠BAC=120°,AB的垂直平分线EF交BC于F,交AB于E.求证:BF=FC.
证明:如图,连接AF.
∵直线EF是AB的垂直平分线,∴BF=AF.
在△ABC中,∵AB=AC,∠BAC=120°,
∴∠B=∠C=(180°-∠BAC)=30°.
又∵FB=FA,
∴∠FAB=∠B=30°,
∴∠CAF=∠BAC-∠BAF=120°-30°=90°.
在△ACF中,∠C=30°,∠CAF=90°,
∴AF=FC,
∴BF=FC.
点拨:在利用含30°角的直角三角形的性质时,一定要先证明这个角所在的三角形是直角三角形,此性质是求线段长度和证明线段倍分关系的重要依据.
当 堂 检 测
1. 在直角△ABC中,∠C=30°,斜边AC的长为5cm,则AB的长为( )
A. 4cm B. 3cm C. 2.5cm D. 2cm
2. 如图,折叠直角三角形纸片的直角,使点C落在斜边AB上的点E处,已知CD=1,∠B=30°,则BD的长是( )
A. 1 B. 2 C. D. 2
第2题 第3题
3. 如图,在△ABC中,∠C=90°,∠B=30°,边AB的垂直平分线DE交AB于点E,交BC于点D,CD=3,则BC的长为( )
A. 6 B. 6 C. 9 D. 3
4. 如图是某商场一楼与二楼之间的手扶电梯示意图,其中AB,CD分别表示一楼、二楼地面的水平线,∠ABC=150°,BC的长是8m,则乘电梯从点B到点C上升的高度h是( )
A. 3m B. 4m C. 5m D. 6m
5. 将一副三角尺如图叠放在一起,若AB=10cm,则阴影部分的面积是 cm2.
6. 如图,孔明同学背着一桶水,从山脚A出发,沿与地面30°角的山坡向上走,送水到山上因受旱缺水的王奶奶家(B处),AB=80米,则孔明从A到B上升的高度BC是 米.
7. 如图,一棵树在一次强台风中于离地面4米处折断倒下,倒下部分与地面成30°夹角,这棵树在折断前的高度为 米.
8. 如图,∠C=90°,∠A=30°,BD⊥AD于D,DC∥AB,AB=10,求CD的长.
9. 如图,已知某船于上午8时在A处观测小岛C在北偏东60°方向上,该船以每小时40海里的速度向东航行到B处,此时测得小岛C在北偏东30°方向上.船以原速度继续向东航行2小时到达小岛C的正南方D处,求船从A处到D处一共走了多少海里.
当堂检测参考答案
1. C 2. B 3. C 4. B
5.
6. 40
7. 12
8. 解:在△ABD中,∵BD⊥AD,∠A=30°,∴BD=AB=×10=5,∠ABD=60°.又∵DC∥AB,∴∠CDB=∠DAB=60°.∵∠C=90°,∴∠CBD=30°,∴CD=BD=×5=2.5.
9. 解:由题意知∠CAD=30°,∠CBD=60°,∠CDA=90°,BD=2×40=80(海里).在△BCD中,∠CBD=60°,∴∠BCD=30°,∴BC=2BD=160海里.由∠CBD=60°,得∠ABC=120°,∵∠CAD=30°,∴∠ACB=30°,∴AB=BC=160海里,∵AD=AB+BD,∴AD=160+80=240(海里).即船从A到D一共走了240海里.
