人教版数学九年级上册第二十四章 圆24.1 圆的有关性质(同步测试含答案)
文档属性
| 名称 | 人教版数学九年级上册第二十四章 圆24.1 圆的有关性质(同步测试含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 151.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-09 00:00:00 | ||
图片预览




文档简介
圆的有关性质 同步练习
1、选择题
1、一条排水管的截面如图所示,已知排水管的半径OB=10,水面宽AB=16,则截面圆心O到水面的距离OC是( )
A.4??????? B.5????????? C.6????????? D.6??
2、如图,点A,B,C,D都在半径为2的⊙O上,若OA4⊥BC, ∠CDA=30°,则弦BC的长为(??? )
A.4????? B.2???????? C.? ????????D.2
3、如图,AB是⊙O直径,若∠AOC =140°,则∠D的度数是? ( )
A.20°?????? B.30°?????C.40°??????? D.70°
4、?如图,AB是⊙O的直径,∠AOC=110°,则∠D=( )
A.25°??????? B.35°???????? C.55°??????? D.70°
5、如图,点A,B,C,在⊙O上,∠ABO=32°,∠ACO=38°,则∠BOC等于(? )
A.60°????????? B.70°?????????? C.120°????????? D.140°
6、?如图,点A、B、C、D都在⊙O上,O点在∠D的内部,四边形OABC为平行四边形,则∠ADC的度数为(? )A.30°?????????? B.45°?????????? C.60°?????????? D.90°?
7、小明不慎把家里的圆形玻璃打碎了,其中四块碎片如图所示,为配到与原来大小一样的圆形玻璃,小明带到商店去的一块玻璃碎片应该是( )
A.第①块? B.第②块? C.第③块? D.第④块
8、如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD,若DE=6,∠BAC+∠EAD=180°,则弦BC的长等于( )
A.8??????? B.10??????? C.11???? D.12
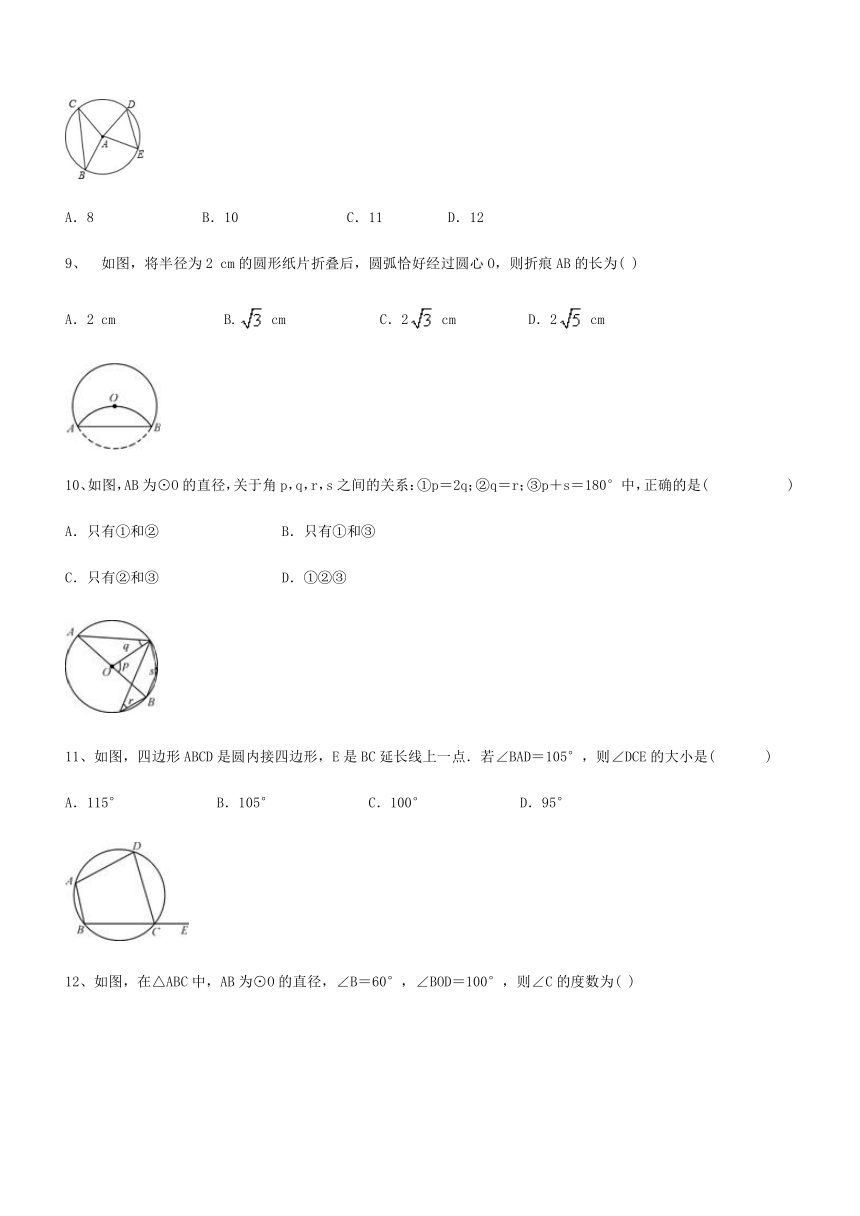
9、?如图,将半径为2 cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为( )
A.2 cm? ?? ??? B. cm? ? ??? C.2 cm ??? ?D.2 cm
?
10、如图,AB为⊙O的直径,关于角p,q,r,s之间的关系:①p=2q;②q=r;③p+s=180°中,正确的是(????? )
A.只有①和②? ??? ??? B.只有①和③
C.只有②和③? ??? ??? D.①②③
?
11、如图,四边形ABCD是圆内接四边形,E是BC延长线上一点.若∠BAD=105°,则∠DCE的大小是( )
A.115°? ? ??? B.105°? ? ??? C.100°? ? ??? D.95°
?
12、如图,在△ABC中,AB为⊙O的直径,∠B=60°,∠BOD=100°,则∠C的度数为( )
A.50°? B.60°? C.70°? D.80°
13、已知一点到圆的最小距离为1 cm,最大距离为3 cm,则圆的半径为(? )
A.1 cm ??? ??? ??? ?B.2 cm? ? ??? ??? C.3 cm? ?? ??? ??? D.1 cm或2 cm
二、填空题
14、如图,四边形ABCD是⊙O的内接四边形,若∠C=140°,则∠BOD= ? °.
1
5、如图,A、B、C是⊙O上的点,若∠AOB=70°,则∠ACB的度数为 ?? .
16、“圆材埋壁”是我国古代著名数学著作《九章算术》中的问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用数学语言可表述为:“如图,CD为的直径,弦AB⊥CD于E,CE=1寸,AB=10寸,求直径CD的长”。(1尺=10寸)则CD=____________
17、如图,AB、BC是⊙O的弦,OM∥BC交AB于M,若∠AOC=100°,则∠AMO= ?? °.
18、如图,AB是⊙O的弦,半径OC⊥AB于点D,且AB=8cm,DC=2cm,则OC= ? ?????cm.?
19、如图,⊙O的直径为10 cm,弦AB=8 cm,P是弦AB上的一个动点,则OP的长度范围为________________.
三、综合题
20、四边形ABCD内接于⊙O,AC为其中一条对角线.
(Ⅰ)如图①,若∠BAD=70°,BC=CD,求∠BAC的大小;
(Ⅱ)如图②,若AD经过圆心O,连接OC,AB=BC,OC∥AB,求∠OCD的大小.
21、如图,AB是半圆O的直径,AB=a,C是半圆上一点,弦AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,连接CD,DB,OD.
(1)求证:△CDF≌△BDE;
(2)当AD= 时,四边形AODC是菱形;
(3)当AD= 时,四边形AEDF是正方形.
22、如图,AB是⊙O的直径,C是的中点,CE⊥AB于E,BD交CE于点F,
(1)求证:CF=BF;
(2)若CD=12,AC=16,求⊙O的半径和CE的长.
参考答案
一、选择题
1、D.
2、D
3、A??
4、B???
5、D
6、C
7、B
8、A.
9、C
10、A
11、B
12、C
13、D
二、填空题
14、80
15、:35°.
16、2尺6寸??????
17、50°
18、? 5??
19、3 cm≤OP≤5 cm
三、综合题
20、解:(Ⅰ)∵四边形ABCD内接于⊙O,BC=CD,
∴∠BAC=∠CAD,
∵∠BAD=70°,
∴∠BAC=∠CAD=35°;
(Ⅱ) 连接BD,如解图,
∵AB=BC,
∴∠BAC=∠BCA,
∵OC∥AB,
∴∠BAC=∠OCA,
∵OA=OC,
∴∠OAC=∠OCA,
∵∠ADB=∠ACB,
∴∠BAC=∠CAO=∠ADB=∠ACO,
∵AD是⊙O的直径,
∴∠ABD=∠ACD=90°,
∴∠ADB+∠BAD=90°,即3∠ACO=90°,
∴∠ACO=30°,
∴∠OCD=∠ACD-∠ACO=90°-30°=60°.
21、(1)证明:∵弦AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,
∴DE=DF.
∵弦AD平分∠BAC,
∴∠FAD=∠BAD,
∴BD=CD.
在Rt△BED和Rt△CFD中,
∴Rt△BED≌Rt△CFD? (HL);
(2)四边形AODC是菱形时,
OD=CD=DB=OB,
∴∠DBA=60°,
∴AD=ABcos∠DBA=asin60°=a,
故答案为:;
(3)当OD⊥AB,即OD与OE重合时,四边形AEDF是正方形,
由勾股定理,得
AD==a,
22、(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
又∵CE⊥AB,
∴∠CEB=90°,
∴∠2=90°﹣∠ABC=∠A,
又∵C是弧BD的中点,
∴∠1=∠A,
∴∠1=∠2,
∴CF=BF;
(2)∵C是弧BD的中点,
∴=,
∴BC=CD=12,
又∵在Rt△ABC中,AC=16,
∴由勾股定理可得:AB=20,
∴⊙O的半径为10,
∵S△ABC=AC?BC=AB?CE,
∴CE==9.6.
同课章节目录
