沪教版(五四学制)八上:17.1 一元二次方程的概念 课件(17张PPT)
文档属性
| 名称 | 沪教版(五四学制)八上:17.1 一元二次方程的概念 课件(17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-09 18:40:49 | ||
图片预览






文档简介
课件17张PPT。17.1一元二次方程的概念学习目标1、理解一元二次方程的概念,
会判断一个方程是否是一元二次方程;
2、知道一元二次方程的一般形式;
3、会判断一个数是否是一元二次方程的根.预习反馈1、满足什么条件的方程是一元二次方程?
2、一元二次方程的一般形式是什么?二次项、二次 项系数、一次项、一次项系数、常数项分别是什么?
3、如何判断一个数是不是一元二次方程的根?
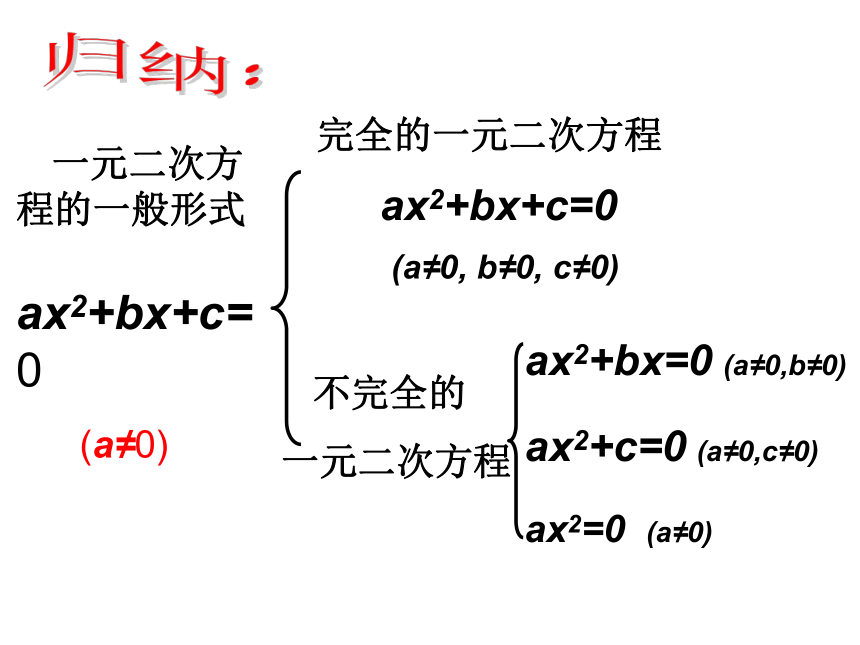
举例说明。ax2+bx=0 (a≠0,b≠0) 一元二次方程的一般形式
ax2+bx+c=0
(a≠0)完全的一元二次方程
ax2+bx+c=0
(a≠0, b≠0, c≠0) 不完全的
一元二次方程ax2+c=0 (a≠0,c≠0)ax2=0 (a≠0)归纳:例1: 判断下列方程是否为一元二次方程?(1)x2+x =36(2) x3+ x2=36(3)x+3y=36(5) x+1=0???????? 判断一个方程是否是一元二次方程,关键是要将方程化为一般式,然后根据一元二次方程必须同时满足的三个条件进行判别。 下列方程中哪些是一元二次方程?是一元二次方程的有:____________练习:可能为0是分式是二次根式二次项、二次项系数、一次项、一次项系数、常数项都是包括符号的 例题2:将下列方程化为一般形式,并分别指出它们的二次项、一次项和常数项及它们的系数:
(1)
(2)解: ax2 + bx + c = 0注意:要确定一元二次方程的系数和常数项 ,必须先将方程化为一般形式二次项系数一次项系数常数项(a≠0) 在写一元二次方程的一般形式时,通常按未知数的次数从高到低排列,即先写二次项,再写一次项,最后是常数项。 方程(2a-4)x2 -2bx+a=0,
①在什么条件下此方程为一元二次方程?
②在什么条件下此方程为一元一次方程? 解:由题意得,2a-4≠0,解之得a≠2∴当a≠2时是一元二次方程;∴当a=2且b≠0时是一元一次方程.例3:4挑战自我 1、下列方程中,关于x的一元二次方程是 ( )A. B. C. D. A (1)三个特征:只含有一个未知数;
方程的两边都是整式;
未知数的最高次数为2次.(2)化简后形如ax2 + bx + c=0(a≠0)叫做一元二次方程.1分2、把下列方程化为一元二次方程的形式,并写出它的二次项系数、一次项系数和常数项:3x2-5x+1=0x2 + x-8=03-5+11+1-83-5 111-87x2 - 4=070 - 42分 3、已知 是方程
的一个解,则 的 值是______。53分4、是关于 的一元二次方程,则m的值为(南京)变式:一元一次方程4分5、已知方程 (m?2) ?(m?2)x?4?0
(1)m为何值时它是一元二次方程?
(2)m为何值时它是一元一次方程?分析:(1)由一元二次方程的一般形式,m2?2?2,故m?2?0,故m??2;
(2)需分三种情况讨论:①m?2?0,此时m?2;②m2?2?1,此时m?? ;③显然x?0,故若m2?2?0,则原方程也是一元一次方程5分讨论:当一元二次方程有一个根为0或1、-1时,一元二次方程的项有什么特征?
会判断一个方程是否是一元二次方程;
2、知道一元二次方程的一般形式;
3、会判断一个数是否是一元二次方程的根.预习反馈1、满足什么条件的方程是一元二次方程?
2、一元二次方程的一般形式是什么?二次项、二次 项系数、一次项、一次项系数、常数项分别是什么?
3、如何判断一个数是不是一元二次方程的根?
举例说明。ax2+bx=0 (a≠0,b≠0) 一元二次方程的一般形式
ax2+bx+c=0
(a≠0)完全的一元二次方程
ax2+bx+c=0
(a≠0, b≠0, c≠0) 不完全的
一元二次方程ax2+c=0 (a≠0,c≠0)ax2=0 (a≠0)归纳:例1: 判断下列方程是否为一元二次方程?(1)x2+x =36(2) x3+ x2=36(3)x+3y=36(5) x+1=0???????? 判断一个方程是否是一元二次方程,关键是要将方程化为一般式,然后根据一元二次方程必须同时满足的三个条件进行判别。 下列方程中哪些是一元二次方程?是一元二次方程的有:____________练习:可能为0是分式是二次根式二次项、二次项系数、一次项、一次项系数、常数项都是包括符号的 例题2:将下列方程化为一般形式,并分别指出它们的二次项、一次项和常数项及它们的系数:
(1)
(2)解: ax2 + bx + c = 0注意:要确定一元二次方程的系数和常数项 ,必须先将方程化为一般形式二次项系数一次项系数常数项(a≠0) 在写一元二次方程的一般形式时,通常按未知数的次数从高到低排列,即先写二次项,再写一次项,最后是常数项。 方程(2a-4)x2 -2bx+a=0,
①在什么条件下此方程为一元二次方程?
②在什么条件下此方程为一元一次方程? 解:由题意得,2a-4≠0,解之得a≠2∴当a≠2时是一元二次方程;∴当a=2且b≠0时是一元一次方程.例3:4挑战自我 1、下列方程中,关于x的一元二次方程是 ( )A. B. C. D. A (1)三个特征:只含有一个未知数;
方程的两边都是整式;
未知数的最高次数为2次.(2)化简后形如ax2 + bx + c=0(a≠0)叫做一元二次方程.1分2、把下列方程化为一元二次方程的形式,并写出它的二次项系数、一次项系数和常数项:3x2-5x+1=0x2 + x-8=03-5+11+1-83-5 111-87x2 - 4=070 - 42分 3、已知 是方程
的一个解,则 的 值是______。53分4、是关于 的一元二次方程,则m的值为(南京)变式:一元一次方程4分5、已知方程 (m?2) ?(m?2)x?4?0
(1)m为何值时它是一元二次方程?
(2)m为何值时它是一元一次方程?分析:(1)由一元二次方程的一般形式,m2?2?2,故m?2?0,故m??2;
(2)需分三种情况讨论:①m?2?0,此时m?2;②m2?2?1,此时m?? ;③显然x?0,故若m2?2?0,则原方程也是一元一次方程5分讨论:当一元二次方程有一个根为0或1、-1时,一元二次方程的项有什么特征?
