沪教版(五四学制)2019-2020学年八年级数学上册期末复习测试卷 (解析版)
文档属性
| 名称 | 沪教版(五四学制)2019-2020学年八年级数学上册期末复习测试卷 (解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-08 14:03:41 | ||
图片预览

文档简介
(真题测试)2019_2020学年八年级数学上册期末考点大串讲(沪教版)
一、填空题
1. (2018-2019学年上海市闵行区? 期末)平面上到原点O的距离是2厘米的点的轨迹是______.
2. (2017-2018学年上海市金山区? 期末)经过已知点P和Q的圆的圆心轨迹是______.
3. (2016-2017学年上海市闵行区九校联考期末 )以线段AB为底边的等腰三角形的顶点的轨迹是______.
4. (2016-2017学年上海市闵行区九校联考? 期末)直角三角形中两边长分别为4和5,那么第三边长为______ .
5. (2016-2017学年上海市闵行区九校联考? 期末)若平面内点A(-1,-3)、B(5,b),且AB=10,则b的值为______ .
6. (2018-2019学年上海市闵行区? 期末)如图,△ABC中,CD⊥AB于D,E是AC的中点.若AD=6,DE=5,则CD的长等于______.
7. (2018-2019学年上海市闵行区? 期末)如图,Rt△ABC中,∠C=90°,BD=2CD,AD是∠BAC的角平分线,∠CAD=______度.
8. (2018-2019学年上海市闵行区? 期末)已知,在△ABC中,AB=,∠C=22.5°,将△ABC翻折使得点A与点C重合,折痕与边BC交于点D,如果DC=2,那么BD的长为______.
9. (2018-2019学年上海市浦东新区期末)如图,△ABC中,AB=AC,∠BAC=120°,AD⊥AC交BC于点D,AD=4,则BC=______.
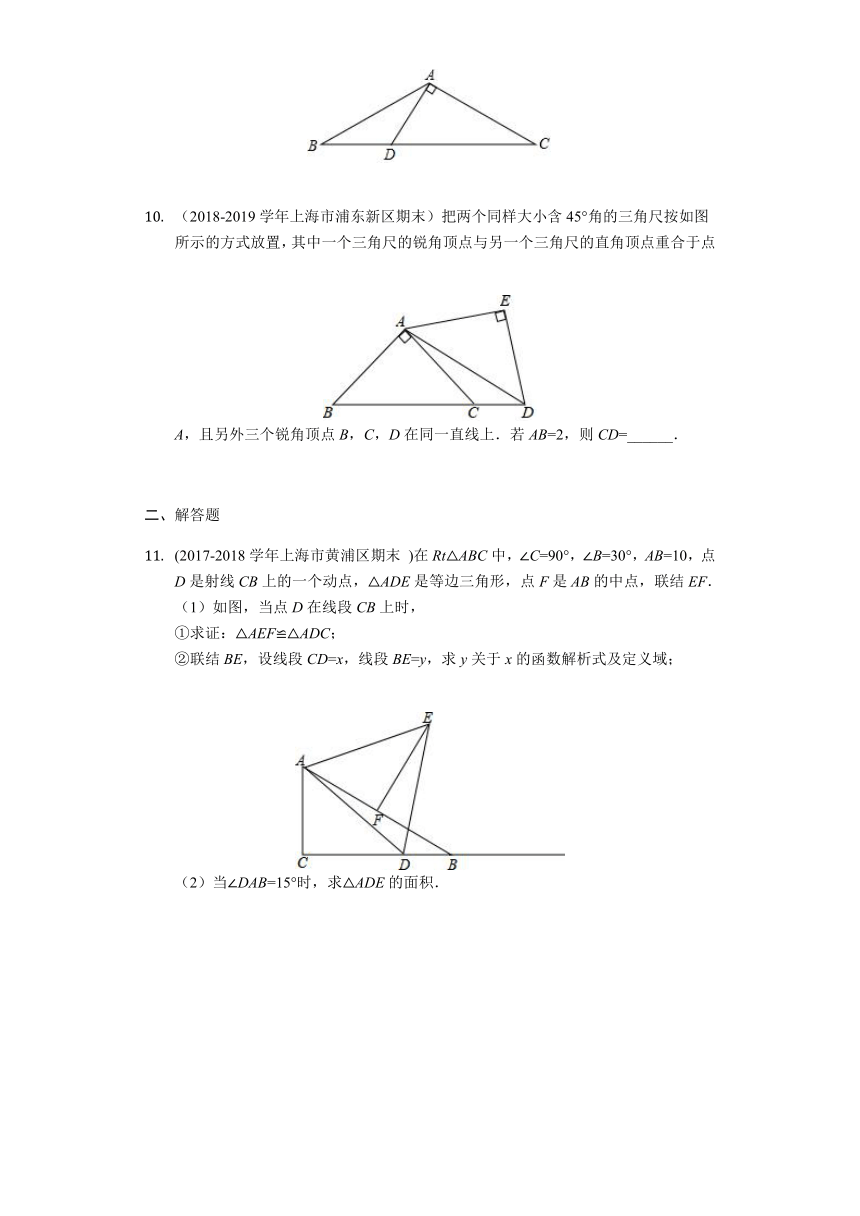
10. (2018-2019学年上海市浦东新区期末)把两个同样大小含45°角的三角尺按如图所示的方式放置,其中一个三角尺的锐角顶点与另一个三角尺的直角顶点重合于点A,且另外三个锐角顶点B,C,D在同一直线上.若AB=2,则CD=______.
二、解答题
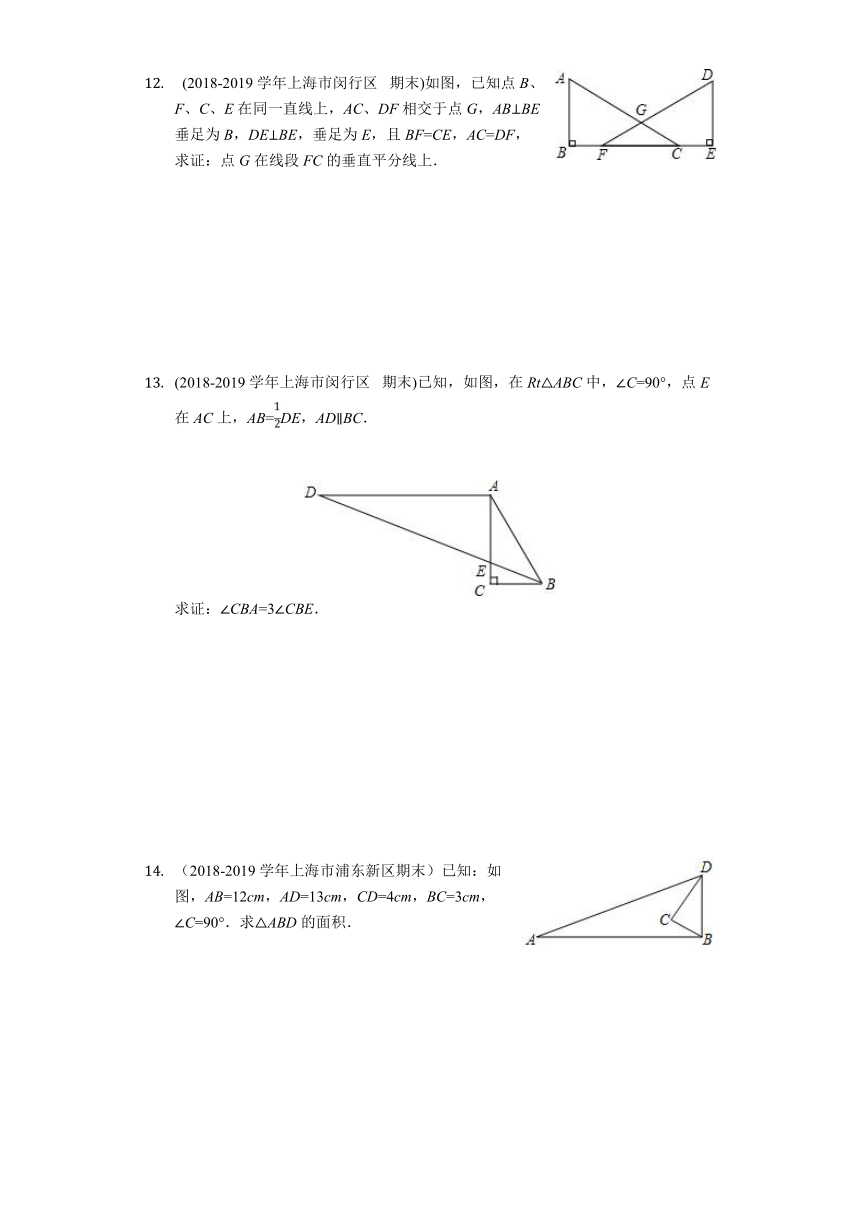
11. (2017-2018学年上海市黄浦区期末 )在Rt△ABC中,∠C=90°,∠B=30°,AB=10,点D是射线CB上的一个动点,△ADE是等边三角形,点F是AB的中点,联结EF.
(1)如图,当点D在线段CB上时,
①求证:△AEF≌△ADC;
②联结BE,设线段CD=x,线段BE=y,求y关于x的函数解析式及定义域;
(2)当∠DAB=15°时,求△ADE的面积.
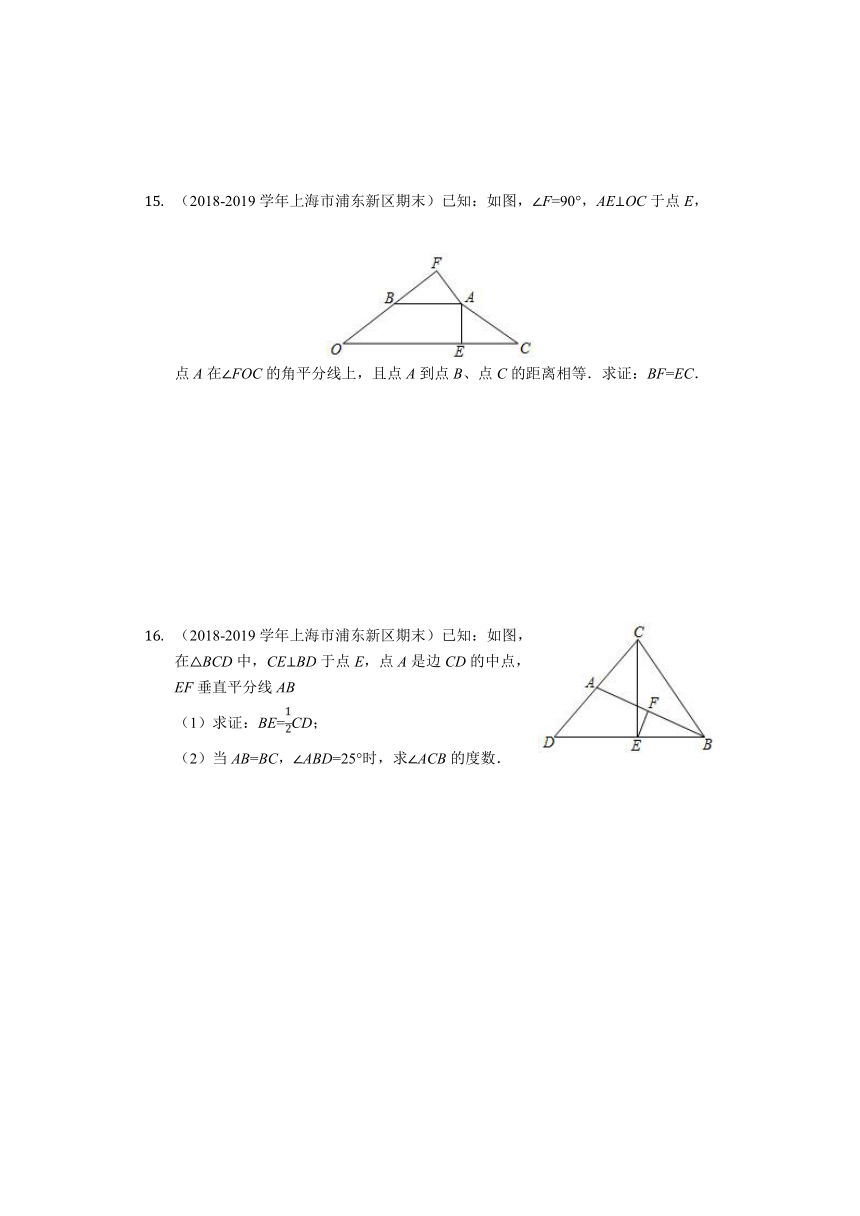
12. (2018-2019学年上海市闵行区? 期末)如图,已知点B、F、C、E在同一直线上,AC、DF相交于点G,AB⊥BE垂足为B,DE⊥BE,垂足为E,且BF=CE,AC=DF,
求证:点G在线段FC的垂直平分线上.
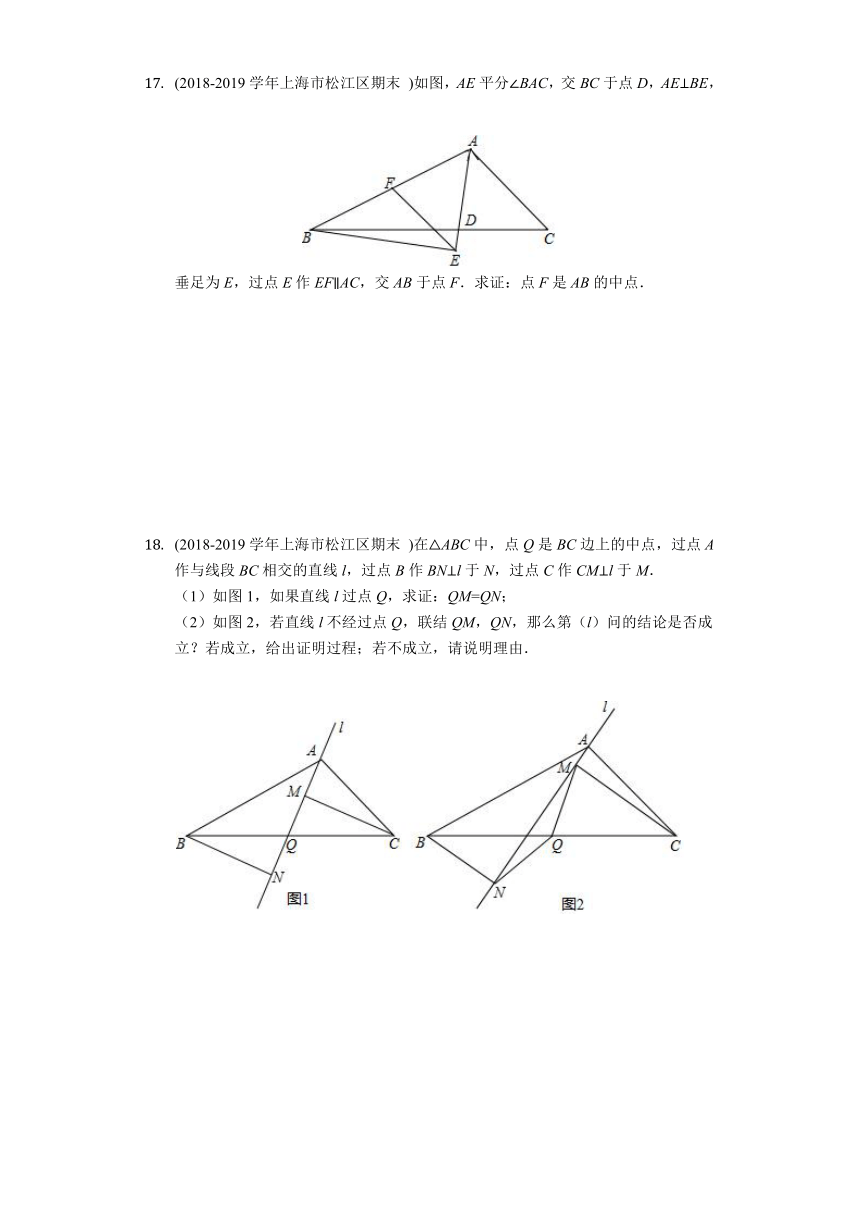
13. (2018-2019学年上海市闵行区? 期末)已知,如图,在Rt△ABC中,∠C=90°,点E在AC上,AB=DE,AD∥BC.
求证:∠CBA=3∠CBE.
14. (2018-2019学年上海市浦东新区期末)已知:如图,AB=12cm,AD=13cm,CD=4cm,BC=3cm,∠C=90°.求△ABD的面积.
15. (2018-2019学年上海市浦东新区期末)已知:如图,∠F=90°,AE⊥OC于点E,点A在∠FOC的角平分线上,且点A到点B、点C的距离相等.求证:BF=EC.
16. (2018-2019学年上海市浦东新区期末)已知:如图,在△BCD中,CE⊥BD于点E,点A是边CD的中点,EF垂直平分线AB
(1)求证:BE=CD;
(2)当AB=BC,∠ABD=25°时,求∠ACB的度数.
17. (2018-2019学年上海市松江区期末 )如图,AE平分∠BAC,交BC于点D,AE⊥BE,垂足为E,过点E作EF∥AC,交AB于点F.求证:点F是AB的中点.
18. (2018-2019学年上海市松江区期末 )在△ABC中,点Q是BC边上的中点,过点A作与线段BC相交的直线l,过点B作BN⊥l于N,过点C作CM⊥l于M.
(1)如图1,如果直线l过点Q,求证:QM=QN;
(2)如图2,若直线l不经过点Q,联结QM,QN,那么第(l)问的结论是否成立?若成立,给出证明过程;若不成立,请说明理由.
19. (2018-2019学年上海市浦东新区第三教育署期末 )已知:如图,BP、CP分别是△ABC的外角平分线,PM⊥AB于点M,PN⊥AC于点N.求证:PA平分∠MAN.
20. (2016-2017学年上海市闵行区九校联考? 期末)已知:如图,在△ABC中,BC=BA,BE平分∠CBA交边CA于点E,∠ABC=45°,CD⊥AB,垂足为D,F为BC中点,BE与DF、DC分别交于点G、H.
(1)求证:BH=CA;
(2)求证:BG2=GE2+EA2.
21. (2018-2019学年上海市长宁区期末 )如图,在Rt△ABC中,已知∠C=90°,∠B=60°,AC=8,点D在边BC上,BD=3CD,线段DB绕点D顺时针旋转α度后(0<α<180),点B旋转至点E,如果点E恰好落在Rt△ABC的边上,求:△DBE的面积.
22. (2018-2019学年上海市浦东新区第四教育署? 期末)已知,如图在△ABC中,AD、BE分别是BC,AC边上的高,AD、BE交于H,DA=DB,BH=AC,点F为BH的中点,∠ABE=15°.
(1)求证:△ADC≌△BDH;
(2)求证:DC=DF.
23. (2018-2019学年上海市浦东新区第四教育署? 期末)已知:如图,AD∥BC,DB平分∠ADC,CE平分∠BCD,交AB于点E,BD于点O.求证:点O到EB与ED的距离相等.
?
24. (2017-2018学年上海市金山区? 期末)直角坐标平面内,已知点A(-1,0)、B(5,4),在y轴上求一点P,使得△ABP是以∠P为直角的直角三角形.
25. (2018-2019学年上海市长宁区期末 )已知,如图,在△ABC中,AE平分∠CAB交BC于点E,AC=6,CE=3,AE=3,BE=5,点F是边AB上的动点(点F与点A,B不重合),连接EF,设BF=x,EF=y.
(1)求AB的长;
(2)求y关于x的函数解析式,并写出函数的定义域;
(3)当△AEF为等腰三角形时,直接写出BF的长.
26. (2018-2019学年上海市金山区期末 )已知,如图,在Rt△ABC中,∠ACB=90°,AB=2,∠B=30°,P是边BC上的一动点,过点P作PE⊥AB,垂足为E,延长PE至点Q,使PQ=PC,连接CQ交边AB于点D.
(1)求AD的长;
(2)设CP=x,△PCQ的面积为y,求y关于x的函数解析式,并写出定义域;
(3)过点C作CF⊥AB,垂足为F,联结PF、QF,试探索当点P在边BC的什么位置时,△PFQ为等边三角形?请指出点P的位置并加以证明.
27. (2018-2019学年上海市松江区期末 )如图,在△ABC中,∠ACB=90°,AC=BC=4,点D是边A上的动点(点D与点A、B不重合),过点D作DE⊥AB交射线BC于点E,联结AE,点F是AE的中点,过点D、F作直线,交AC于点G,联结CF、CD.
(1)当点E在边BC上,设,DB=x,CE=y.
①写出y关于x的函数关系式及定义域;
②判断△CDF的形状,并给出证明;
(2)如果AE=,求DG的长.
28. (2018-2019学年上海市浦东新区第三教育署期末 )如图,在△ABC中,∠ACB=90°,∠A=30°,D是边AC上不与点A、C重合的任意一点,DE⊥AB,垂足为点E,M是BD的中点.
(1)求证:CM=EM;
(2)如果BC=,设AD=x,CM=y,求y与x的函数解析式,并写出函数的定义域;
(3)当点D在线段AC上移动时,∠MCE的大小是否发生变化?如果不变,求出∠MCE的大小;如果发生变化,说明如何变化.
29. (2018-2019学年上海市嘉定区期末 )如图,在△ABC中,∠ACB=90°,∠A=30°,AB=4,点P是AB边上一个动点,过点P作AB的垂线交AC边与点D,以PD为边作∠DPE=60°,PE交BC边与点E.
(1)当点D为AC边的中点时,求BE的长;
(2)当PD=PE时,求AP的长;
(3)设AP的长为x,四边形CDPE的面积为y,请直接写出y与x的函数解析式及自变量x的取值范围.
30. (2018-2019学年上海市闵行区? 期末)如图,已知在Rt△ABC中,∠ABC=90°,AB=3,BC=4,AD∥BC,将一个直角的顶点置于点C,并将它绕着点C旋转,直角的两边分别交AB的延长线于点E,交射线AD于点F,联结EF交BC于点G,设BE=x.
(1)旋转过程中,当点F与点A重合时,求BE的长;
(2)若AF=y,求y关于x的函数关系式及定义域;
(3)旋转过程中,若CF=GC,求此时BE的长.
31. (2017-2018学年上海市金山区? 期末)已知:如图,在△ABC中,∠ACB=90°,AC=6,BC=2.D是AC上一个动点,过点D作DE⊥AB交AB于F,且DE=DC,联结CE交AB于G(点G不与点F重合).
(1)求∠A的度数;
(2)求BG的长;
(3)设CD=x,GF=y,求y与x的函数关系式并写出x的取值范围.
(2016-2017学年上海市闵行区九校联考? 期末)如图,在△ABC中,∠ACB=90°,∠A=30°,D是边AC上不与点A、C重合的任意一点,DE⊥AB,垂足为点E,M是BD的中点.
(1)求证:CM=EM;
(2)如果BC=,设AD=x,CM=y,求y与x的函数解析式,并写出函数的定义域;
(3)当点D在线段AC上移动时,∠MCE的大小是否发生变化?如果不变,求出∠MCE的大小;如果发生变化,说明如何变化.
32.
答案和解析
1.【答案】以原点O为圆心,2厘米长为半径的圆
【解析】解:平面上到原点O的距离是2厘米的点的轨迹是以点O为圆心,2厘米长为半径的圆.
故答案为:以原点O为圆心,2厘米长为半径的圆.
根据圆的定义就可解决问题.
本题主要考查的是圆的定义,其中圆是到定点的距离等于定长的点的集合.
2.【答案】线段PQ的垂直平分线
【解析】解:根据同圆的半径相等,则圆心应满足到点P和点Q的距离相等,即经过已知点P和点Q的圆的圆心的轨迹是线段PQ的垂直平分线.
故答案为:线段PQ的垂直平分线.
要求作经过已知点P和点Q的圆的圆心,则圆心应满足到点P和点Q的距离相等,从而根据线段的垂直平分线性质即可求解.
此题考查了点的轨迹问题,熟悉线段垂直平分线的性质.
3.【答案】线段AB的垂直平分线(与AB的交点除外)
【解析】解:∵△ABC以线段AB为底边,CA=CB,
∴点C在线段AB的垂直平分线上,除去与AB的交点(交点不满足三角形的条件),
∴以线段AB为底边的等腰三角形的顶点C的轨迹是线段AB的垂直平分线,不包括AB的中点.
故答案为线段AB的垂直平分线,不包括AB的中点.
满足△ABC以线段AB为底边且CA=CB,根据线段的垂直平分线判定得到点C在线段AB的垂直平分线上,除去与AB的交点(交点不满足三角形的条件).
本题考查了轨迹:轨迹是动点按一定条件运动所经过的痕迹.也考查了线段的垂直平分线判定与性质,.解题的关键是熟记线段AB的垂直平分线的定义.
4.【答案】3或
【解析】解:当5是斜边时,则第三边是=3,
当4和5都是直角边时,则第三边是=.
故答案为:3或.
考虑两种情况:4和5都是直角边或5是斜边,根据勾股定理进行求解.
此类题注意考虑两种情况,熟练运用勾股定理进行计算.
5.【答案】-11或5
【解析】解:由题意可得,
,
解得,b=-11或b=5,
故答案为:-11或5.
根据题意和两点间的距离公式可以求得b的值,本题得以解决.
本题考查两点间的距离公式,解题的关键是明确题意、明确两点间的距离公式.
6.【答案】8
【解析】解:如图,∵△ABC中,CD⊥AB于D,E是AC的中点,DE=5,
∴DE=AC=5,
∴AC=10.
在直角△ACD中,∠ADC=90°,AD=6,AC=10,则根据勾股定理,得
CD===8.
故答案是:8.
由“直角三角形斜边上的中线等于斜边的一半”求得AC=2DE=10;然后在直角△ACD中,利用勾股定理来求线段CD的长度即可.
本题考查了勾股定理,直角三角形斜边上的中线.利用直角三角形斜边上的中线等于斜边的一半求得AC的长度是解题的难点.
7.【答案】30
【解析】解:过点D作DE⊥AB于E点,
∵AD是∠BAC的角平分线,DC⊥AC,DE⊥AB,
∴DC=DE.
∵BD=2CD,
∴BD=2DE.
∴∠B=30°.
∵∠C=90°,
∴∠CAB=60°.
∴∠CAD=×60°=30°.
故答案为30.
过点D作DE⊥AB于E点,根据角平分线性质可得DE=DC,从而BD=2DE,则∠B=30°,可知∠CAB=60°,再利用角平分线的定义可求∠CAD度数.
本题主要考查了角平分线的性质、根据角平分线的性质作垂线段的解题的关键.
8.【答案】+1或-1
【解析】解:分两种情况:
①当∠B为锐角时,如图所示,过A作AF⊥BC于F,
由折叠可得,折痕DE垂直平分AC,
∴AD=CD=2,
∴∠ADB=2∠C=45°,
∴△ADF是等腰直角三角形,
∴AF=DF=,
又∵AB=,
∴Rt△ABF中,BF==1,
∴BD=BF+DF=1+;
②当∠ABC为钝角时,如图所示,过A作AF⊥BC于F,
同理可得,△ADF是等腰直角三角形,
∴AF=DF=,
又∵AB=,
∴Rt△ABF中,BF==1,
∴BD=DF-BF=-1;
故答案为:+1或-1.
过A作AF⊥BC于F,构造直角三角形,分两种情况讨论,利用勾股定理以及等腰直角三角形的性质,即可得到BD的长.
本题主要考查了折叠问题以及勾股定理的运用,解决问题的关键是分两种情况画出图形进行求解.解题时注意:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.
9.【答案】12
【解析】解:∵△ABC中,AB=AC,∠BAC=120°,
∴∠C=∠B=30°,
∵AD⊥AC交BC于点D,
∴CD=2AD=8,∠BAD=30°=∠B,
∴BD=AD=4,
∴BC=BD+CD=4+8=12.
故答案为:12.
依据等腰三角形的内角和,即可得到∠C=∠B=30°,依据AD⊥AC交BC于点D,即可得到CD=2AD=8,∠BAD=30°=∠B,进而得出BC的长.
本题主要考查了含30°角的直角三角形的性质以及等腰三角形的性质,解题时注意:在直角三角形中,30°角所对的直角边等于斜边的一半.
10.【答案】-
【解析】解:如图,过点A作AF⊥BC于F,
在Rt△ABC中,∠B=45°,
∴BC=AB=2,BF=AF=AB=,
∵两个同样大小的含45°角的三角尺,
∴AD=BC=2,
在Rt△ADF中,根据勾股定理得,DF==,
∴CD=BF+DF-BC=+-2=-,
故答案为:-.
先利用等腰直角三角形的性质求出BC=2,BF=AF=,再利用勾股定理求出DF,即可得出结论.
此题主要考查了勾股定理,等腰直角三角形的性质,正确作出辅助线是解本题的关键.
11.【答案】(1)①证明:在Rt△ABC中,
∵∠B=30°,AB=10,
∴∠CAB=60°,AC=AB=5,
∵点F是AB的中点,
∴AF=AB=5,
∴AC=AF,
∵△ADE是等边三角形,
∴AD=AE,∠EAD=60°,
∵∠CAB=∠EAD,即∠CAD+∠DAB=∠FAE+∠DAB,
∴∠CAD=∠FAE,
在△AEF和△ADC中,
,
∴△AEF≌△ADC(SAS);
②∵△AEF≌△ADC,
∴∠AEF=∠C=90°,EF=CD=x,
又∵点F是AB的中点,
∴AE=BE=y,
在Rt△AEF中,勾股定理可得:y2=25+x2,
∴函数的解析式是y=,定义域是0<x≤5;
(2)①当点在线段CB上时,
由∠DAB=15°,可得∠CAD=45°,△ADC是等腰直角三角形,
∴AD2=50,
△ADE的面积为;
②当点在线段CB的延长线上时,
由∠DAB=15°,可得∠ADB=15°,BD=BA=10,
∴在Rt△ACD中,勾股定理可得AD2=200+100,
△ADE的面积为50+75,
综上所述,△ADE的面积为或50+75.
【解析】(1)①在直角三角形ABC中,由30度所对的直角边等于斜边的一半求出AC的长,再由F为AB中点,得到AC=AF=5,确定出三角形ADE为等边三角形,利用等式的性质得到一对角相等,砸由AD=AE,利用SAS即可得证;
②由全等三角形对应角相等得到∠AEF为直角,EF=CD=x,在三角形AEF中,利用勾股定理即可列出y关于x的函数解析式及定义域;
(2)分两种情况考虑:①当点在线段CB上时;②当点在线段CB的延长线上时,分别求出三角形ADE面积即可.
此题考查了勾股定理,全等三角形的判定与性质,以及等边三角形的性质,熟练掌握勾股定理是解本题的关键.
12.【答案】证明:∵BF=CE,
∴BF+FC=CE+FC,即BC=EF.
又∵AB⊥BE,DE⊥BE,
∴∠B=∠E=90°.
在Rt△ABC和Rt△DEF中,,
∴Rt△ABC≌Rt△DEF??(HL)
∴∠ACB=∠DFE(全等三角形的对应角相等),
∴GF=GC(等角对等边),
∴点G在线段FC的垂直平分线上.
【解析】证得Rt△ABC≌Rt△DEF(HL),推知∠ACB=∠DFE,然后由“等角对等边”证得GF=GC,即可得出结论.
本题考查了全等三角形的判定与性质、等腰三角形的判定与性质;熟练掌握等腰三角形的判定与性质,证明三角形全等是解题的关键.
13.【答案】证明:
取DE的中点F,连接AF,
∵AD∥BC,∠ACB=90°,
∴∠DAE=∠ACB=90°,
∴AF=DF=EF=DE,
∵AB=DE,
∴DF=AF=AB,
∴∠D=∠DAF,∠AFB=∠ABF,
∴∠AFB=∠D+∠DAF=2∠D,
∴∠ABF=2∠D,
∵AD∥BC,
∴∠CBE=∠D,
∴∠CBA=∠CBE+∠ABF=3∠CBE.
【解析】取DE的中点F,连接AF,根据直角三角形的性质求出AF=DF=FE=DE,推出DF=AF=AB,根据等腰三角形的性质求出∠D=∠DAF,∠AFB=∠ABF,求出∠ABF=2∠D,∠CBE=∠D,即可得出答案.
本题考查了等腰三角形的性质,直角三角形的性质,平行线的性质,三角形的外角性质的应用,能正确作出辅助线是解此题的关键,难度适中.
14.【答案】解:∵CD=4cm,BC=3cm,∠C=90°,
∴BD=cm,
∵AB=12cm,AD=13cm,
∴BD2+AB2=AD2,
∴∠ABD=90°,
∴.
【解析】根据勾股定理的逆定理证明△ABD是直角三角形,即可求解.
此题主要是考查了勾股定理及其逆定理.关键是根据勾股定理的逆定理证明△ABD是直角三角形.
15.【答案】证明:∵点A在∠FOC的角平分线上,∠F=90°,AE⊥OC,
∴AE=AF,
∵点A到点B、点C的距离相等,
∴AB=AC,
∵∠F=∠AEC=90°,
∴Rt△ABF≌Rt△ACE(HL),
∴BF=EC.
【解析】证明Rt△ABF≌Rt△ACE(HL)即可解决问题.
本题考查全等三角形的判定和性质,角平分线的性质定理等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.
16.【答案】(1)证明:连接AE,
∵CE⊥BD,点A是边CD的中点,
∴AE=AD=CD,
∵EF垂直平分线AB,
∴EA=EB,
∴BE=CD;
(2)∵EA=EB,
∴∠EAB=∠ABD=25°,
∴∠AED=∠EAB+∠ABD=50°,
∵EA=AD,
∴∠D=∠AED=50°,
∴∠BAC=∠ABD+∠D=75°,
∵AB=BC,
∴∠ACB=∠BAC=75°.
【解析】(1)连接AE,根据直角三角形的性质得到AE=AD=CD,根据线段垂直平分线的性质得到EA=EB,等量代换证明结论;
(2)根据等腰三角形的性质、三角形的外角性质求出∠AED,根据等腰三角形的性质计算,得到答案.
本题考查的是直角三角形的性质、线段垂直平分线的性质、三角形的外角性质,掌握直角三角形斜边上的中线是斜边的一半是解题的关键.
17.【答案】证明:∵AE平分∠BAC,
∴∠BAD=∠CAD,
∵EF∥AC,
∴∠FEA=∠CAD,
∴∠BAD=∠FEA,
∴FA=FE,
∵AE⊥BE,
∴∠BEF+∠AEF=90°,
∵∠ABE+∠BAE=90°,
∴∠ABE=∠BEF,
∴FB=FE,
∴FB=FA,即点F是AB的中点.
【解析】根据角平分线的性质、平行线的性质得到FA=FE,根据垂直的定义、同角的余角相等得到FB=FE,证明结论.
本题考查的是平行线的性质、等腰三角形的性质、线段的中点,掌握等腰三角形的性质定理是解题的关键.
18.【答案】证明:(1)∵点Q是BC边上的中点,
∴BQ=CQ,
∵BN⊥l,CM⊥l,
∴∠BNQ=∠CMQ=90°,且BQ=CQ,∠BQN=∠CQM,
∴△BQN≌△CQM(AAS)
∴QM=QN;
(2)仍然成立,
理由如下:
如图,延长NQ交CM于E,
∵点Q是BC边上的中点,
∴BQ=CQ,
∵BN⊥l,CM⊥l,
∴BN∥CM
∴∠NBQ=∠QCM,且BQ=CQ,∠BQN=∠CQE,
∴△BQN≌△CQE(ASA)
∴QE=QN,且∠NME=90°,
∴QM=NQ=QE.
【解析】(1)由“AAS”可证△BQN≌△CQM,可得QM=QN;
(2)延长NQ交CM于E,由“ASA”可证△BQN≌△CQE,可得QE=QN,由直角三角形的性质可得结论.
本题考查了全等三角形的判定和性质,直角三角形的性质,添加恰当辅助线构造全等三角形是本题的关键.
19.【答案】证明:作PD⊥BC于点D,
∵BP是△ABC的外角平分线,PM⊥AB,PD⊥BC,
∴PM=PD,
同理,PN=PD,
∴PM=PN,又PM⊥AB,PN⊥AC,
∴PA平分∠MAN.
【解析】作PD⊥BC于点D,根据角平分线的性质得到PM=PD,PN=PD,得到PM=PN,根据角平分线的判定定理证明即可.
本题考查的是角平分线的判定和性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.
20.【答案】解:(1)∵BC=BA,BE平分∠CBA,
∴BE⊥CA,
∴∠BEA=90°,
又CD⊥AB,∠ABC=45°,
∴∠BDC=∠CDA=90°,
∴∠BCD=∠ABC=45°,∠BAC+∠DCA=90°,∠BAC+∠ABE=90°,
∴DB=DC,∠ABE=∠DCA.
∵在△DBH与△DCA中,
∵,
∴△DBH≌△DCA(ASA),
∴BH=AC;
(2)如图,连接CG,AG.
∵AB=BC,BE⊥AC,
∴BE垂直平分AC,
∴AG=CG.
又∵F点是BC的中点,DB=DC,
∴DF垂直平分BC,
∴BG=CG,
∴AG=BG.
在Rt△AGE中,∵AG2=GE2+EA2,
∴BG2=GE2+EA2.
【解析】(1)由等腰三角形的性质知∠BEA=90°,根据直角三角形的性质即余角的性质得DB=DC、∠ABE=∠DCA,利用ASA证出△DBH≌△DCA即可;
(2)证BE垂直平分AC,则由“垂直平分线上任意一点,到线段两端点的距离相等”推知AG=CG.易证DF垂直平分BC,则BG=CG,所以依据等量代换证得AG=BG,在Rt△AGE中,由勾股定理即可推出答案.
本题考查了勾股定理,等腰三角形性质,全等三角形的性质和判定,线段的垂直平分线的性质的应用,注意:线段垂直平分线上的点到线段两端的距离相等,等腰三角形具有三线合一的性质,主要考查学生运用定理进行推理的能力.
21.【答案】解:∵∠C=90°,∠B=60°,
∴∠A=30°,
∴AB=2BC
∵在Rt△ABC中,AB2=BC2+AC2,
∴4BC2=BC2+64×3,
∴BC=8,
∴AB=16,
∵点D在边BC上,BD=3CD,
∴BD=6,CD=2,
如图,当点E在AB上时,过点E作EF⊥BC于点F,
∵旋转
∴DE=BD=6,且∠ABC=60°,
∴△BDE是等边三角形
∴BE=6,且EF⊥BD,∠ABC=60°,
∴BF=3,EF=BF=3
∴S△BED=BD×EF=9,
如图,当点E在AC上时,
∵旋转
∴BD=DE=6
在Rt△CDE中,CE===4,
∴S△BED=BD×EC=12,
综上所述:△DBE的面积为12或9.
【解析】根据勾股定理可求AB,BC的长,即可求BD=6,CD=2,分点E落在AB上,或AC上两种情况讨论,根据勾股定理和等边三角形的性质以及三角形面积公式可求△DBE的面积.
本题考查了旋转的性质,直角三角形的性质,等腰三角形的性质,勾股定理等知识,灵活运用相关的性质定理、综合运用知识是解题的关键.
22.【答案】证明:(1)∵AD⊥BC,BE⊥AC,
∴∠ADC=∠BDH=90°,
在Rt△ADC和Rt△BDH中,
,
∴△ADC≌△BDH(HL);
(2)∵DB=DA,
∴∠DBA=∠DAB=45°,
∵∠ABE=15°,
∴∠DBH=30°,
∴DH=BH,
∵BF=FH,
∴DF=BH,
∴DF=DH,
∵△ADC≌△BDH;
∴CD=DH,
∴DC=DF.
【解析】本题考查直角三角形斜边中线的性质,直角三角形30度角的性质等,全等三角形的判定和性质知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
(1)由全等三角形的判定定理HL证得结论即可;
(2)结合(1)中全等三角形的对应边相等得到DC=DH,然后根据含30度角的直角三角形的性质以及直角三角形斜边中线的性质证明即可;
23.【答案】证明:∵AD∥BC,
∴∠ADC+∠BCD=180°,
∵DB平分∠ADC,CE平分∠BCD,
∴∠ODC+∠OCD=90°,
∴∠DOC=90°,又CE平分∠BCD,
∴CE是BD的垂直平分线,
∴EB=ED,又∠DOC=90°,
∴EC平分∠BED,
∴点O到EB与ED的距离相等.
【解析】根据平行线的性质和角平分线的定义得到∠DOC=90°,根据等腰三角形的三线合一证明即可.
本题考查的是平行线的性质、角平分线的性质,掌握平行线的判定定理和性质定理是解题的关键.
24.【答案】解:设P(0,y)
由勾股定理得,AB2=(5+1)2+42,AP2=12+y2,BP2=52+(4-y)2,
∵∠P=90°,
∴AB2=AP2+BP2,即(5+1)2+42=12+y2+52+(4-y)2,
解得,y1=5,y2=-1,
∴当点P的坐标为(0,5)或P(0,-1)时,△ABP是以∠P为直角的直角三角形.
【解析】设P(0,y),根据勾股定理用y表示出AP、BP,根据勾股定理列出方程,解方程得到答案.
本题考查的是勾股定理、坐标与图形性质,如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2.
25.【答案】解:(1)∵AC=6,CE=3,AE=3,
∴AC2+CE2=62+32=45,
AE2=(3)2=45,
∴AC2+CE2=AE2,
∴∠ACE=90°,
∵BE=5,
∴BC=8,
由勾股定理得:AB===10;
(2)如图1,过E作EG⊥AB于G,
∵AE平分∠BAC,∠C=90°,
∴EG=EC=3,
∵AE=AE,
∴Rt△ACE≌Rt△AGE(HL),
∴AG=AC=6,
∴BG=10-6=4,
∵BF=x,
∴FG=|4-x|,
在Rt△EFG中,由勾股定理得:EF=,
∴y==(0<x<10);
(3)分两种情况讨论:
①当AE=AF=3时,如图2,
∵AB=10,
∴BF=10-3,
②当AF=EF时,如图3,过F作FP⊥AE于P,
∴AP=AE=,
∵∠CAE=∠FAP,∠APF=∠C=90°,
∴△ACE∽△APF,
∴,即,
AF=,
∴BF=10-=,
综上,当△AEF为等腰三角形时,BF的长为10-3或.
【解析】(1)先根据勾股定理的逆定理可得∠ACE=90°,再由勾股定理计算AB的长;
(2)作辅助线,构建三角形全等,先根据角平分线的性质得:EG=CE=3,表示FG的长,因为F可能在G的左边或右边,所以FG=|4-x|,最后根据勾股定理可得y关于x的函数解析式;
(3)当△AEF为等腰三角形时,存在两种情况:①当AE=AF=3时,如图2,②当AF=EF时,如图3,分别根据等腰三角形的性质可得结论.
本题属于三角形综合题,考查了全等三角形的性质和判定,角平分线的性质定理,勾股定理及其逆定理,等腰三角形的判定和性质等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型.
26.【答案】解:(1)∵∠ACB=90°,∠B=30°,
∴AC=AB=1,
∵PQ=PC,
∴∠PQC=∠PCQ,
∵PE⊥AB,
∴∠PQC+∠QDE=90°,
∵∠ACB=90°,
∴∠PCQ+∠ACD=90°,
∴∠ACD=∠QDE,
∵∠ACD=∠ADC,
∴∠ACD=∠ADC,
∴AD=AC=1;
(2)作QH⊥BC于H,
∵∠ACB=90°,∠B=30°,
∴∠A=60°,又AD=AC,
∴△ADC为等边三角形,
∴∠QCB=30°,
∵PQ=PC=x,
∴∠PQC=∠PCQ=30°,
∴∠QPH=60°,
∴QH=x,
∴△PCQ的面积为y=×x×x=x2(<x<);
(3)当点P在边BC的中点时,△PFQ为等边三角形,
理由如下:如备用图,∵∠BFC=90°,点P是BC的中点,
∴PF=BC=CP,
∵∠BFC=90°,∠B=30°,
∴FC=BC=CP,∠BPE=60°,
∴FC=PF=CP,
∴△FPC为等边三角形,
∴∠FPC=60°,
∵∠BPE=60°,
∴∠QPF=60°,
∵PF=PC=PQ,
∴△PFQ为等边三角形.
【解析】(1)根据直角三角形的性质求出AC,根据直角三角形的性质、等腰三角形的判定定理解答即可;
(2)作QH⊥BC于H,根据直角三角形的性质用x表示出QH,根据三角形的面积公式计算,得到答案;
(3)证明△FPC为等边三角形,得到∠FPC=60°,根据等腰三角形的判定定理证明结论.
本题考查的是直角三角形的性质、等边三角形的判定和性质、三角形的面积计算,掌握等边三角形的判定定理和性质定理是解题的关键.
27.【答案】解:(1)①∵∠ACB=90°,AC=BC=4,
∴AB=4,∠B=∠BAC=45°,
又∵DE⊥AB,
∴△DEB为等腰直角三角形,
∵DB=x,CE=y,
∴EB=x,
又∵EB+CE=4,
∴x+y=4,
∴y=4-x(0<x≤2);
②∵DE⊥AB,∠ACB=90°,
∴∠ADE=90°,
∵点F是AE的中点,
∴CF=AF=AE,DF=AF=AE,
∴CF=DF,
∵∠CFE=2∠CAE,∠EFD=2∠EAD,
∴∠CFD=∠CFE+∠EFD=2∠CAE+2∠EAD=2∠CAD,
∵∠CAB=45°,
∴∠CFD=90°,
∴△CDF是等腰直角三角形;
(2)如图1,当点E在BC上时,AE=,AC=4,
在Rt△ACE中,CE=,
则AE=2CE,
∴∠CAE=30°,
又CF=DF=AE=,
在Rt△CFG中,GF=,
∴DG=DF+FG=;
如图2,当点E在BC延长线上时,∠CFD=90°,
同理可得CF=DF=AE=,
在Rt△CFG中,GF=,
∴DG=DF-FG=.
【解析】(1)①先证△DEB为等腰直角三角形,设DB=x,CE=y知EB=x,由EB+CE=4知x+y=4,从而得出答案;
②由∠ADE=90°,点F是AE的中点知CF=AF=AE,DF=AF=AE,据此得出CF=DF,再由∠CFE=2∠CAE,∠EFD=2∠EAD知∠CFD=∠CFE+∠EFD=2∠CAE+2∠EAD=2∠CAD,结合∠CAB=45°知∠CFD=90°,据此可得答案;
(2)分点E在BC上和BC延长线上两种情况,分别求出DF、GF的长,从而得出答案.
本题主要是三角形的综合问题,解题的关键是掌握等腰直角三角形的判定和性质、勾股定理、直角三角形的性质等知识点.
28.【答案】(1)证明:∵在Rt△ABC中,∠ACB=90°,M是BD的中点,
∴CM=BD.
同理ME=BD,
∴CM=ME.
(2)解:∵在Rt△ABC中,∠ACB=90°,∠A=30°,BC=,
∴AB=2BC=2.
由勾股定理得AC=3,
∵AD=x,∴CD=3-x,
在Rt△BCD中,∠BCD=90°,
∴BD2=BC2+CD2,
∴BD=,
∵CM=BD,CM=y,
∴y=(0<x<3),
(3)不变.
∵M是Rt△BCD斜边BD的中点,∴MB=MC,∴∠MBC=∠MCB.
∴∠CMD=∠MBC+∠MCB=2∠MBC,
∵M是Rt△BED斜边BD的中点,
同理可得:∠EMD=2∠MBE,
∠CMD+∠EMD=2∠MBC+2∠MBE=2(∠MBC+∠MBE)=2∠ABC,
即∠CME=2∠ABC=120°,
∵MC=ME,
∴∠MCE=∠MEC=30°.
【解析】(1)根据直角三角形斜边的中线等于斜边的一半即可证明;
(2)根据CM=BD,可得BD=2y,根据勾股定理又可得出BD用x表示的形式,换成等式即可得出y与x的函数解析式;
(3)根据(1)可知,∠MBC=∠MCB,∠MEB=∠MBE,易得出∠CMD=2∠CBM,∠DME=2∠MBE,即∠CME=2∠CBA是定值,又知CM=ME,即可证明∠MCE是定值,即可得出结论.
本题考查了直角三角形斜边上的中线,含30°角的直角三角形以及勾股定理的知识,难度较大,熟练掌握各个知识点是解答本题的关键.
29.【答案】解:(1)在△ABC中,∠ACB=90°,∠A=30°,AB=4,
∴BC=AB=2,
∴AC==2,
∵D是AC的中点,
∴AD=,DP=,AP=,
∴BP=AB-AP=,
∵∠DPE=60°,
∴∠EPB=30°,
∴EB=BP=;
(2)设AP=x,则BP=4-x,
在两个有30°的Rt△APD,Rt△BPE中,AD=2DP,BP=2BE,
由勾股定理解得PD=x,PE=(4-x),
因为PD=PE,
所以x=(4-x),
解得x=,即AP=;
(3)由(2)知:AP=x,PD=x,PE=(4-x),BE=(4-x),
∴y=S△ABC-S△APD-S△BPE
=×2×2-?x?x-×(4-x)?(4-x)
=-x2+x(0<x<3).
【解析】(1)由∠A=30°,AB=4求得BC=2,AC=2,结合D是AC中点知AD=,DP=,AP=,从而得出BP=AB-AP=,再根据∠EPB=30°可得答案;
(2)设AP=x,知BP=4-x,由勾股定理解得PD=x,PE=(4-x),根据PD=PE得出关于x的方程,解之可得;
(3)由(2)知:AP=x,PD=x,PE=(4-x),BE=(4-x),依据y=S△ABC-S△APD-S△BPE可得答案.
本题是四边形的综合问题,解题的关键是掌握直角三角形的有关性质、勾股定理、三角形的面积公式等知识点.
30.【答案】解:(1)如图1,∵∠ABC=90°,AB=3,BC=4,
∴AC==5,
∵∠ACE=90°,
∴AC2=AB?AE,
∴52=3AE,
∴AE=,
∴BE=AE-AB=-3=;
(2)过F作FH⊥BC于H,
∵AD∥BC,
∴∠BAD=∠CBE=90°,
∴∠FAB=∠ABH=∠BHF=90°,
∴四边形ABHF是矩形,
∴FH=AB=3,BH=AF=y,
∴CH=4-y,
∵∠FCE=90°,
∴∠FCH+∠ECB=∠ECB+∠BEC=90°,
∴∠FCH=∠BEC,
∴△CFH∽△ECB,
∴,
∴,
∴y=x-4,(0≤x≤);
(3)∵CF=GC,
∴∠CGF=∠CFG,
∵AD∥BC,
∴∠AFE=∠CGF,
∴∠CFG=∠AFE,
∵∠FAE=∠FCE=90°,
∴CE=AE=3+x,
在Rt△BCE中,
∵BC2+BE2=CE2,
∴(x+3)2=x2+42,
∴x=,
∴BE=.
【解析】(1)如图1,根据勾股定理得到AC==5,根据射影定理即可得到结论;
(2)过F作FH⊥BC于H,根据平行线的性质得到∠BAD=∠CBE=90°,根据矩形的性质得到FH=AB=3,BH=AF=y,求得CH=4-y,根据相似三角形的性质即可得到结论;
(3)根据等腰三角形的性质和平行线的性质得到∠CFG=∠AFE,根据角平分线的性质得到CE=AE=3+x,根据勾股定理即可得到结论.
本题考查几何变换综合题、相似三角形的判定和性质、矩形的判定和性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,学会正确寻找相似三角形解决问题,学会用方程的思想思考问题,属于中考压轴题.
31.【答案】解:(1)∵∠ACB=90°,AC=6,BC=2,
∴AB====4,
∴BC=AB,
∴∠A=30°;
(2)∵DE⊥AB,
∴∠AFD=90°,
∵∠A=30°,
∴∠ADF=60°,
∴∠CDE=120°,
∵DE=DC,
∴∠DCE=∠DEC=30°
∴∠GCB=60°,
又∵∠A+∠B=90°,
∴∠B=60°,
∴△BCG是等边三角形,
∴GB=CB=2;
(3)∵AC=6,CD=x,
∴AD=6-x,
则AF===AD=(6-x),
∵GF=AB-AF-BG,
∴y=4-(6-x)-2=x-,
由y≥0知x-≥0,解得x≥2,
所以x的取值范围是2≤x≤6.
【解析】(1)利用勾股定理求得AB=4,从而知BC=AB,据此可得答案;
(2)由∠A=30°知∠CDE=120°,由DE=DC知∠GCB=60°,结合∠B=60°知△BCG是等边三角形,从而得出答案;
(3)由AD=6-x知AF=AD=(6-x),根据GF=AB-AF-BG得y=4-(6-x)-2=x-,由y≥0可得x≥2,结合x≤6可得取值范围.
本题是三角形的综合问题,解题的关键是掌握直角三角形的性质,勾股定理,等边三角形的判定与性质等知识点.
32.【答案】(1)证明:∵在Rt△ABC中,∠ACB=90°,M是BD的中点,
∴CM=BD.
同理ME=BD,
∴CM=ME.
(2)解:∵在Rt△ABC中,∠ACB=90°,∠A=30°,BC=,
∴AB=2BC=2.
由勾股定理得AC=3,
∵AD=x,∴CD=3-x,
在Rt△BCD中,∠BCD=90°,
∴BD2=BC2+CD2,
∴BD=,
∵CM=BD,CM=y,
∴y=(0<x<3),
(3)不变.
∵M是Rt△BCD斜边BD的中点,∴MB=MC,∴∠MBC=∠MCB.
∴∠CMD=∠MBC+∠MCB=2∠MBC,
∵M是Rt△BED斜边BD的中点,
同理可得:∠EMD=2∠MBE,
∠CMD+∠EMD=2∠MBC+2∠MBE=2(∠MBC+∠MBE)=2∠ABC,
即∠CME=2∠ABC=120°,
∵MC=ME,
∴∠MCE=∠MEC=30°.
【解析】(1)根据直角三角形斜边的中线等于斜边的一半即可证明;
(2)根据CM=BD,可得BD=2y,根据勾股定理又可得出BD用x表示的形式,换成等式即可得出y与x的函数解析式;
(3)根据(1)可知,∠MBC=∠MCB,∠MEB=∠MBE,易得出∠CMD=2∠CBM,∠DME=2∠MBE,即∠CME=2∠CBA是定值,又知CM=ME,即可证明∠MCE是定值,即可得出结论.
本题考查了直角三角形斜边上的中线,含30°角的直角三角形以及勾股定理的知识,难度较大,熟练掌握各个知识点是解答本题的关键.
