人教版八年级上数学教学讲义,复习补习资料(巩固练习):02【提高】与三角形有关的线段
文档属性
| 名称 | 人教版八年级上数学教学讲义,复习补习资料(巩固练习):02【提高】与三角形有关的线段 |  | |
| 格式 | zip | ||
| 文件大小 | 263.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-08 14:10:43 | ||
图片预览

文档简介
与三角形有关的线段(提高)知识讲解
【学习目标】
1. 理解三角形及与三角形有关的概念,掌握它们的文字、符号语言及图形表述方法;
2. 理解并会应用三角形三边间的关系;
3. 理解三角形的高、中线、角平分线及重心的概念,学会它们的画法及简单应用;
4. 对三角形的稳定性有所认识,知道这个性质有广泛的应用.
与三角形有关的线段(提高)巩固练习
【巩固练习】
一、选择题
1.如果三条线段的比是:①1:3:4;②1:2:3;③1:4:6;④3:3:6;⑤6:6:10;⑥3:4:5,其中可构成三角形的有( )
A.1个 B.2个 C.3个 D.4个
2.一个三角形的周长是偶数,其中的两条边分别为5和9,则满足上述条件的三角形个数为 ( )
A.2个 B.4个 C.6个 D.8个
3.(2019春?成安县期末)下列说法正确的是( )
①三角形的三条中线都在三角形内部;②三角形的三条角平分线都在三角形内部;③三角形三条高都在三角形的内部.
A.①②③ B.①② C.②③ D.①③
4.如图,AC⊥BC,CD⊥AB,DE⊥BC,则下列说法中错误的是 ( )
A.在△ABC中,AC是BC边上的高
B.在△BCD中,DE是BC边上的高
C.在△ABE中,DE是BE边上的高
D.在△ACD中,AD是CD边上的高
/
5.(2019春?南长区期中)有4根小木棒,长度分别为3cm、5cm、7cm、9cm任意取其中的3根小木棒首尾相接搭三角形,可搭出不同的三角形的个数为( )
A.2个 B.3个 C.4个 D.5个
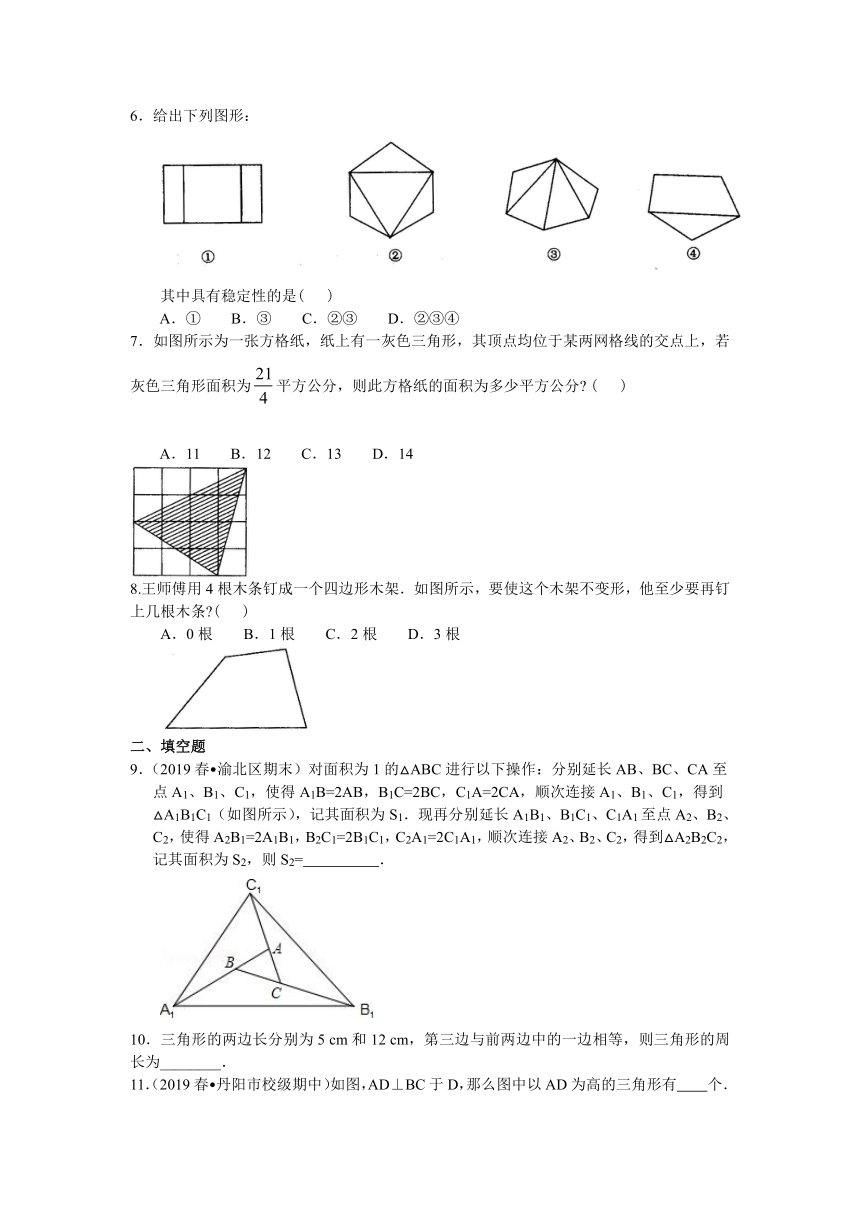
6.给出下列图形:
/
其中具有稳定性的是( )
A.① B.③ C.②③ D.②③④
7.如图所示为一张方格纸,纸上有一灰色三角形,其顶点均位于某两网格线的交点上,若灰色三角形面积为/平方公分,则此方格纸的面积为多少平方公分? ( )
A.11 B.12 C.13 D.14
/
8.王师傅用4根木条钉成一个四边形木架.如图所示,要使这个木架不变形,他至少要再钉上几根木条?( )
A.0根 B.1根 C.2根 D.3根
/
二、填空题
9.(2019春?渝北区期末)对面积为1的△ABC进行以下操作:分别延长AB、BC、CA至点A1、B1、C1,使得A1B=2AB,B1C=2BC,C1A=2CA,顺次连接A1、B1、C1,得到△A1B1C1(如图所示),记其面积为S1.现再分别延长A1B1、B1C1、C1A1至点A2、B2、C2,使得A2B1=2A1B1,B2C1=2B1C1,C2A1=2C1A1,顺次连接A2、B2、C2,得到△A2B2C2,记其面积为S2,则S2= .
/
10.三角形的两边长分别为5 cm和12 cm,第三边与前两边中的一边相等,则三角形的周长为________.
11.(2019春?丹阳市校级期中)如图,AD⊥BC于D,那么图中以AD为高的三角形有 个.
/
12.在数学活动中,小明为了求/…/的值(结果用n表示),设计了如图所示的几何图形.请你利用这个几何图形求/…/=________.
/
13.请你观察下图的变化过程,说明四边形的四条边一定时,其面积________确定.(填“能”或“不能”)
/
14.如图,是用四根木棒搭成的平行四边形框架,AB=8cm,AD=6cm,使AB固定,转动AD,当∠DAB=_____时,ABCD的面积最大,最大值是________.
/
三、解答题
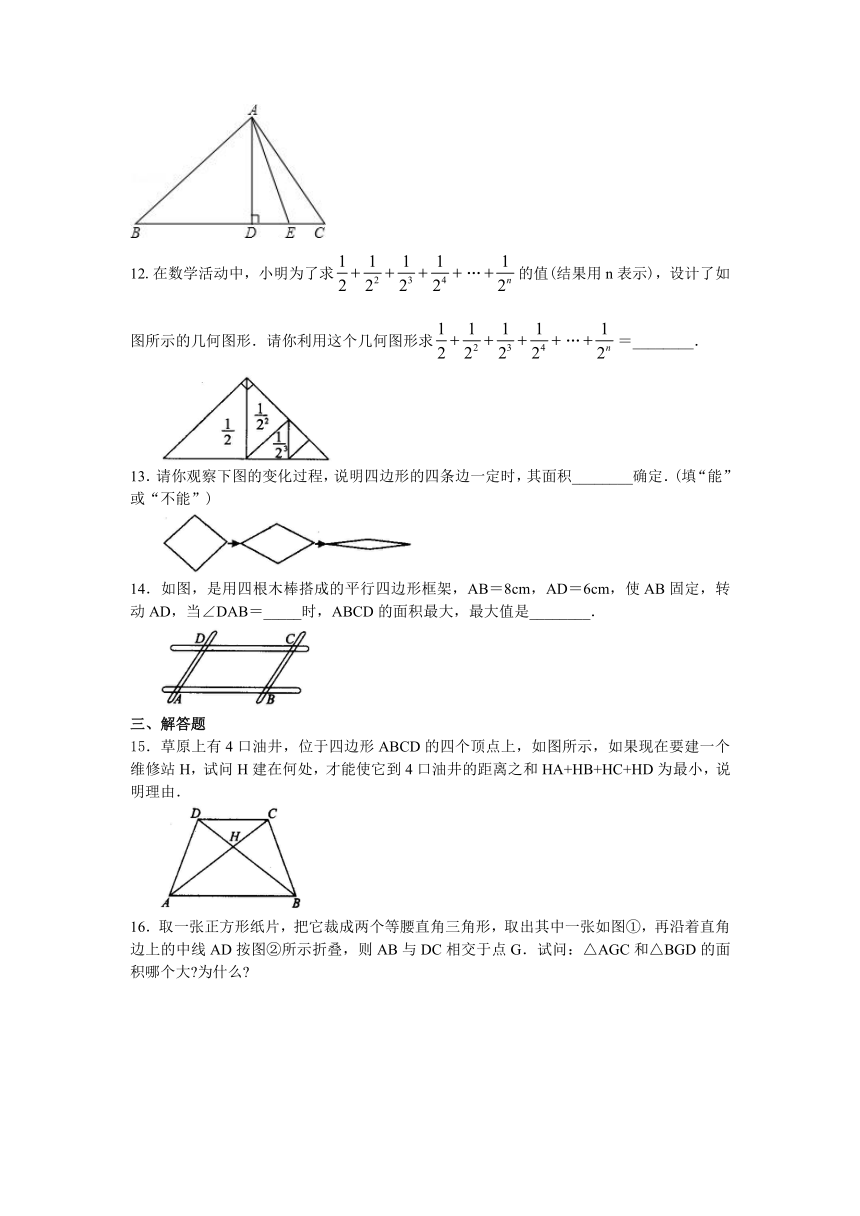
15.草原上有4口油井,位于四边形ABCD的四个顶点上,如图所示,如果现在要建一个维修站H,试问H建在何处,才能使它到4口油井的距离之和HA+HB+HC+HD为最小,说明理由.
/
16.取一张正方形纸片,把它裁成两个等腰直角三角形,取出其中一张如图①,再沿着直角边上的中线AD按图②所示折叠,则AB与DC相交于点G.试问:△AGC和△BGD的面积哪个大?为什么?
/
17. 已知AD是△ABC的高,∠BAD=70°,∠CAD=20°,
(1)求∠BAC的度数.
(2)△ABC是什么三角形.
18. (2019春?西城区期末)阅读下列材料:
某同学遇到这样一个问题:如图1,在△ABC中,AB=AC,BD是△ABC的高.P是BC边上一点,PM,PN分别与直线AB,AC垂直,垂足分别为点M,N.求证:BD=PM+PN.
他发现,连接AP,有S△ABC=S△ABP+S△ACP,即/AC?BD=/AB?PM+/AC?PN.由AB=AC,可得BD=PM+PN.
他又画出了当点P在CB的延长线上,且上面问题中其他条件不变时的图形,如图2所示.他猜想此时BD,PM,PN之间的数量关系是:BD=PN﹣PM.
/
请回答:
(1)请补全以下该同学证明猜想的过程;
证明:连接AP.
∵S△ABC=S△APC﹣ ,
∴/AC?BD=/AC? ﹣/AB? .
∵AB=AC,
∴BD=PN﹣PM.
(2)参考该同学思考问题的方法,解决下列问题:
在△ABC中,AB=AC=BC,BD是△ABC的高.P是△ABC所在平面上一点,PM,PN,PQ分别与直线AB,AC,BC垂直,垂足分别为点M,N,Q.
①如图3,若点P在△ABC的内部,则BD,PM,PN,PQ之间的数量关系是: ;
②若点P在如图4所示的位置,利用图4探究得出此时BD,PM,PN,PQ之间的数量关系是: .
【答案与解析】
一、选择题
1. 【答案】B;
【解析】根据两边之和大于第三边:⑤⑥满足.
2. 【答案】B;
【解析】5+9=14,所以第三边长应为偶数,大于4而小于14的偶数有4个,所以
3. 【答案】B;
【解析】①、②正确;而对于三角形三条高:锐角三角形的三条高在三角形的内部;直角三角形有两条高在边上;钝角三角形有两条高在外部,故③错误.
4. 【答案】C;
【解析】三角形高的定义.
5. 【答案】B;
【解析】解:可搭出不同的三角形为:3cm、5cm、7cm;3cm、5cm、9cm;3cm、7cm、9cm;5cm、7cm、9cm共4个,其中3cm、5cm、9cm不能组成三角形,故选B.
6. 【答案】C;
【解析】均是由三角形构成的图形,具有稳定性.
7. 【答案】B;
【解析】设每个小正方形的边长为a,则有16a2-4 a×2 a÷2-3 a×2 a÷2-4 a×a÷2=/,解得a2=/,而整个方格纸的面积为16a2=12(平方公分).
8. 【答案】B;
二、填空题
9. 【答案】361;
【解析】解:连接A1C,根据A1B=2AB,得到:AB:A1A=1:3,
因而若过点B,A1作△ABC与△AA1C的AC边上的高,则高线的比是1:3,
因而面积的比是1:3,则△A1BC的面积是△ABC的面积的2倍,
设△ABC的面积是a,则△A1BC的面积是2a,
同理可以得到△A1B1C的面积是△A1BC面积的2倍,是4a,
则△A1B1B的面积是6a,
同理△B1C1C和△A1C1A的面积都是6a,
△A1B1C1的面积是19a,
即△A1B1C1的面积是△ABC的面积的19倍,
同理△A2B2C2的面积是△A1B1C1的面积的19倍,
∴S2=19×19×1=361.
故答案为:361.
/
10.【答案】29cm;
11.【答案】6;
12.【答案】/;
【答案】解:如图所示,设大三角形的面积为1,然后不断地按顺序作出各个三角形的中线,根据三角形的中线把它分成两个面积相等的三角形可知,/…/表示组成面积为1的大三角形的n个小三角形的面积之和,因此/…/=/.
13.【答案】不能;
【解析】因为四边形的高不能确定.
14.【答案】90°, 48 cm2;
三、解答题
15.【解析】
解:维修站应建在四边形两对角线AC、BD的交点H处,理由如下:取不同于H的F点,根据三角形两边之和大于第三边可得;FD+FB>HD+HB,FC+FA>HC+HA.
所以:FD+FB+FC+FA>HD+HB+HC+HA,
即HD+HB+HC+HA为最小.
16.【解析】
解:∵ BD=CD,∴ /.
∴ /.
∴ /.
17.【解析】
解:(1)当高AD在△ABC的内部时(如图(1)).
因为∠BAD=70°,∠CAD=20°,所以∠BAC=∠BAD+∠CAD=70°+20°=90°.
/
当高AD在△ABC的外部时(如图(2)).
因为∠BAD=70°,∠CAD=20°,
所以∠BAC=∠BAD-∠CAD=70°-20°=50°.
综上可知∠BAC的度数为90°或50°.
(2)如图(1),当AD在△ABC的内部时,
因为∠BAC=∠BAD+∠CAD=70°+20°=90°,
所以△ABC是直角三角形.
如图(2),当AD在△ABC的外部时,
因为∠BAC=∠BAD-∠CAD=70°-20°=50°,
∠ABC=90°-∠BAD=90°-70°=20°,
所以∠ACB=180°-∠ABC-∠BAC=180°-50°-20°=110°.
所以△ABC为钝角三角形.
综上可知,△ABC是直角三角形或钝角三角形.
18.【解析】解:(1)证明:连接AP.
∵S△ABC=S△APC﹣S△APB,
∴/AC?BD=/AC?PN﹣/AB?PM.
∵AB=AC,
∴BD=PN﹣PM.
(2)①BD=PM+PN+PQ;
如图3,连接AP、BP、CP,
∵S△ABC=S△APC+S△APB+S△BPC
∴/AC?BD=/AC?PN+/AB?PM+/BC?PQ,
∵AB=AC=BC,
∴BD=PM+PN+PQ;
②BD=PM+PQ﹣PN;
如图4,连接AP、BP、CP,
∵S△ABC=S△APB+S△BPC﹣S△APC.
∵/AC?BD=/AB?PM+/BC?PQ﹣/AC?PN,
∵AB=AC=BC,
∴BD=PM+PQ﹣PN.
/
【学习目标】
1. 理解三角形及与三角形有关的概念,掌握它们的文字、符号语言及图形表述方法;
2. 理解并会应用三角形三边间的关系;
3. 理解三角形的高、中线、角平分线及重心的概念,学会它们的画法及简单应用;
4. 对三角形的稳定性有所认识,知道这个性质有广泛的应用.
与三角形有关的线段(提高)巩固练习
【巩固练习】
一、选择题
1.如果三条线段的比是:①1:3:4;②1:2:3;③1:4:6;④3:3:6;⑤6:6:10;⑥3:4:5,其中可构成三角形的有( )
A.1个 B.2个 C.3个 D.4个
2.一个三角形的周长是偶数,其中的两条边分别为5和9,则满足上述条件的三角形个数为 ( )
A.2个 B.4个 C.6个 D.8个
3.(2019春?成安县期末)下列说法正确的是( )
①三角形的三条中线都在三角形内部;②三角形的三条角平分线都在三角形内部;③三角形三条高都在三角形的内部.
A.①②③ B.①② C.②③ D.①③
4.如图,AC⊥BC,CD⊥AB,DE⊥BC,则下列说法中错误的是 ( )
A.在△ABC中,AC是BC边上的高
B.在△BCD中,DE是BC边上的高
C.在△ABE中,DE是BE边上的高
D.在△ACD中,AD是CD边上的高
/
5.(2019春?南长区期中)有4根小木棒,长度分别为3cm、5cm、7cm、9cm任意取其中的3根小木棒首尾相接搭三角形,可搭出不同的三角形的个数为( )
A.2个 B.3个 C.4个 D.5个
6.给出下列图形:
/
其中具有稳定性的是( )
A.① B.③ C.②③ D.②③④
7.如图所示为一张方格纸,纸上有一灰色三角形,其顶点均位于某两网格线的交点上,若灰色三角形面积为/平方公分,则此方格纸的面积为多少平方公分? ( )
A.11 B.12 C.13 D.14
/
8.王师傅用4根木条钉成一个四边形木架.如图所示,要使这个木架不变形,他至少要再钉上几根木条?( )
A.0根 B.1根 C.2根 D.3根
/
二、填空题
9.(2019春?渝北区期末)对面积为1的△ABC进行以下操作:分别延长AB、BC、CA至点A1、B1、C1,使得A1B=2AB,B1C=2BC,C1A=2CA,顺次连接A1、B1、C1,得到△A1B1C1(如图所示),记其面积为S1.现再分别延长A1B1、B1C1、C1A1至点A2、B2、C2,使得A2B1=2A1B1,B2C1=2B1C1,C2A1=2C1A1,顺次连接A2、B2、C2,得到△A2B2C2,记其面积为S2,则S2= .
/
10.三角形的两边长分别为5 cm和12 cm,第三边与前两边中的一边相等,则三角形的周长为________.
11.(2019春?丹阳市校级期中)如图,AD⊥BC于D,那么图中以AD为高的三角形有 个.
/
12.在数学活动中,小明为了求/…/的值(结果用n表示),设计了如图所示的几何图形.请你利用这个几何图形求/…/=________.
/
13.请你观察下图的变化过程,说明四边形的四条边一定时,其面积________确定.(填“能”或“不能”)
/
14.如图,是用四根木棒搭成的平行四边形框架,AB=8cm,AD=6cm,使AB固定,转动AD,当∠DAB=_____时,ABCD的面积最大,最大值是________.
/
三、解答题
15.草原上有4口油井,位于四边形ABCD的四个顶点上,如图所示,如果现在要建一个维修站H,试问H建在何处,才能使它到4口油井的距离之和HA+HB+HC+HD为最小,说明理由.
/
16.取一张正方形纸片,把它裁成两个等腰直角三角形,取出其中一张如图①,再沿着直角边上的中线AD按图②所示折叠,则AB与DC相交于点G.试问:△AGC和△BGD的面积哪个大?为什么?
/
17. 已知AD是△ABC的高,∠BAD=70°,∠CAD=20°,
(1)求∠BAC的度数.
(2)△ABC是什么三角形.
18. (2019春?西城区期末)阅读下列材料:
某同学遇到这样一个问题:如图1,在△ABC中,AB=AC,BD是△ABC的高.P是BC边上一点,PM,PN分别与直线AB,AC垂直,垂足分别为点M,N.求证:BD=PM+PN.
他发现,连接AP,有S△ABC=S△ABP+S△ACP,即/AC?BD=/AB?PM+/AC?PN.由AB=AC,可得BD=PM+PN.
他又画出了当点P在CB的延长线上,且上面问题中其他条件不变时的图形,如图2所示.他猜想此时BD,PM,PN之间的数量关系是:BD=PN﹣PM.
/
请回答:
(1)请补全以下该同学证明猜想的过程;
证明:连接AP.
∵S△ABC=S△APC﹣ ,
∴/AC?BD=/AC? ﹣/AB? .
∵AB=AC,
∴BD=PN﹣PM.
(2)参考该同学思考问题的方法,解决下列问题:
在△ABC中,AB=AC=BC,BD是△ABC的高.P是△ABC所在平面上一点,PM,PN,PQ分别与直线AB,AC,BC垂直,垂足分别为点M,N,Q.
①如图3,若点P在△ABC的内部,则BD,PM,PN,PQ之间的数量关系是: ;
②若点P在如图4所示的位置,利用图4探究得出此时BD,PM,PN,PQ之间的数量关系是: .
【答案与解析】
一、选择题
1. 【答案】B;
【解析】根据两边之和大于第三边:⑤⑥满足.
2. 【答案】B;
【解析】5+9=14,所以第三边长应为偶数,大于4而小于14的偶数有4个,所以
3. 【答案】B;
【解析】①、②正确;而对于三角形三条高:锐角三角形的三条高在三角形的内部;直角三角形有两条高在边上;钝角三角形有两条高在外部,故③错误.
4. 【答案】C;
【解析】三角形高的定义.
5. 【答案】B;
【解析】解:可搭出不同的三角形为:3cm、5cm、7cm;3cm、5cm、9cm;3cm、7cm、9cm;5cm、7cm、9cm共4个,其中3cm、5cm、9cm不能组成三角形,故选B.
6. 【答案】C;
【解析】均是由三角形构成的图形,具有稳定性.
7. 【答案】B;
【解析】设每个小正方形的边长为a,则有16a2-4 a×2 a÷2-3 a×2 a÷2-4 a×a÷2=/,解得a2=/,而整个方格纸的面积为16a2=12(平方公分).
8. 【答案】B;
二、填空题
9. 【答案】361;
【解析】解:连接A1C,根据A1B=2AB,得到:AB:A1A=1:3,
因而若过点B,A1作△ABC与△AA1C的AC边上的高,则高线的比是1:3,
因而面积的比是1:3,则△A1BC的面积是△ABC的面积的2倍,
设△ABC的面积是a,则△A1BC的面积是2a,
同理可以得到△A1B1C的面积是△A1BC面积的2倍,是4a,
则△A1B1B的面积是6a,
同理△B1C1C和△A1C1A的面积都是6a,
△A1B1C1的面积是19a,
即△A1B1C1的面积是△ABC的面积的19倍,
同理△A2B2C2的面积是△A1B1C1的面积的19倍,
∴S2=19×19×1=361.
故答案为:361.
/
10.【答案】29cm;
11.【答案】6;
12.【答案】/;
【答案】解:如图所示,设大三角形的面积为1,然后不断地按顺序作出各个三角形的中线,根据三角形的中线把它分成两个面积相等的三角形可知,/…/表示组成面积为1的大三角形的n个小三角形的面积之和,因此/…/=/.
13.【答案】不能;
【解析】因为四边形的高不能确定.
14.【答案】90°, 48 cm2;
三、解答题
15.【解析】
解:维修站应建在四边形两对角线AC、BD的交点H处,理由如下:取不同于H的F点,根据三角形两边之和大于第三边可得;FD+FB>HD+HB,FC+FA>HC+HA.
所以:FD+FB+FC+FA>HD+HB+HC+HA,
即HD+HB+HC+HA为最小.
16.【解析】
解:∵ BD=CD,∴ /.
∴ /.
∴ /.
17.【解析】
解:(1)当高AD在△ABC的内部时(如图(1)).
因为∠BAD=70°,∠CAD=20°,所以∠BAC=∠BAD+∠CAD=70°+20°=90°.
/
当高AD在△ABC的外部时(如图(2)).
因为∠BAD=70°,∠CAD=20°,
所以∠BAC=∠BAD-∠CAD=70°-20°=50°.
综上可知∠BAC的度数为90°或50°.
(2)如图(1),当AD在△ABC的内部时,
因为∠BAC=∠BAD+∠CAD=70°+20°=90°,
所以△ABC是直角三角形.
如图(2),当AD在△ABC的外部时,
因为∠BAC=∠BAD-∠CAD=70°-20°=50°,
∠ABC=90°-∠BAD=90°-70°=20°,
所以∠ACB=180°-∠ABC-∠BAC=180°-50°-20°=110°.
所以△ABC为钝角三角形.
综上可知,△ABC是直角三角形或钝角三角形.
18.【解析】解:(1)证明:连接AP.
∵S△ABC=S△APC﹣S△APB,
∴/AC?BD=/AC?PN﹣/AB?PM.
∵AB=AC,
∴BD=PN﹣PM.
(2)①BD=PM+PN+PQ;
如图3,连接AP、BP、CP,
∵S△ABC=S△APC+S△APB+S△BPC
∴/AC?BD=/AC?PN+/AB?PM+/BC?PQ,
∵AB=AC=BC,
∴BD=PM+PN+PQ;
②BD=PM+PQ﹣PN;
如图4,连接AP、BP、CP,
∵S△ABC=S△APB+S△BPC﹣S△APC.
∵/AC?BD=/AB?PM+/BC?PQ﹣/AC?PN,
∵AB=AC=BC,
∴BD=PM+PQ﹣PN.
/
