人教版八年级上数学教学讲义,复习补习资料(巩固练习):03【提高】与三角形有关的角
文档属性
| 名称 | 人教版八年级上数学教学讲义,复习补习资料(巩固练习):03【提高】与三角形有关的角 |

|
|
| 格式 | zip | ||
| 文件大小 | 212.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-08 14:12:03 | ||
图片预览


文档简介
与三角形有关的角(提高)知识讲解
【学习目标】
1.理解三角形内角和定理的证明方法;
2.掌握三角形内角和定理及三角形的外角性质;
3.能够运用三角形内角和定理及三角形的外角性质进行相关的计算,证明问题.
与三角形有关的角(提高)巩固练习
【巩固练习】
一、选择题
1.如图所示,一根直尺EF压在三角板30°的角∠BAC上,与两边AC,AB交于M,N.那么∠CME+∠BNF是( )
A.150° B.180° C.135° D.不能确定
2.若一个三角形的三个内角互不相等,则它的最小角必小于( )
A.30° B.45° C.60° D.55°
3.下列语句中,正确的是( )
A.三角形的外角大于任何一个内角
B.三角形的外角等于这个三角形的两个内角之和
C.三角形的外角中,至少有两个钝角
D.三角形的外角中,至少有一个钝角
4.如果一个三角形的两个外角之和为270°,那么这个三角形是 ( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法确定
5.(2019春?泰山区期中)具备下列条件的△ABC中,不是直角三角形的是 ( )
A.∠A+∠B=∠C B.∠A=∠B=∠C
C.∠A:∠B:∠C=1:2:3 D.∠A=2∠B=3∠C
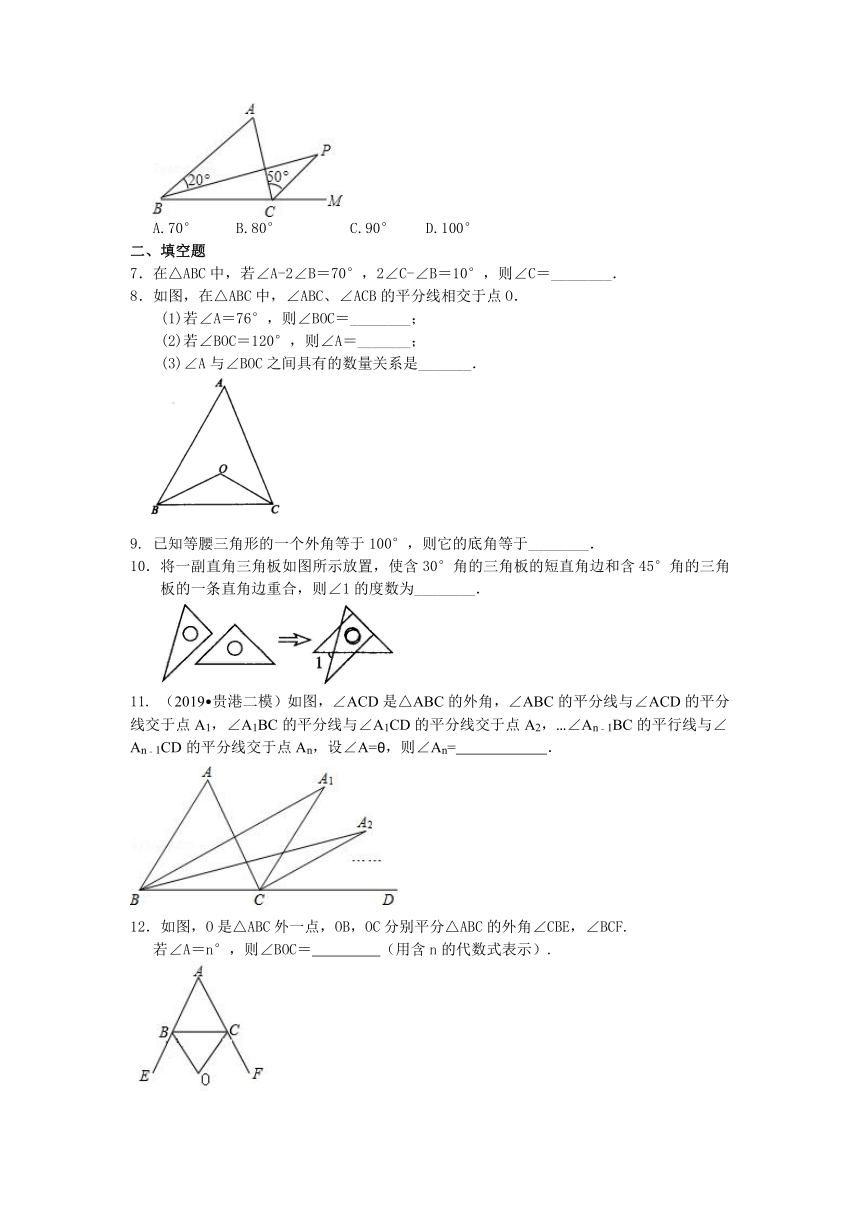
6.(2019春?泰山区期中)如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP=20°,∠ACP=50°,则∠A+∠P=( )
A.70° B.80° C.90° D.100°
二、填空题
7.在△ABC中,若∠A-2∠B=70°,2∠C-∠B=10°,则∠C=________.
8.如图,在△ABC中,∠ABC、∠ACB的平分线相交于点O.
(1)若∠A=76°,则∠BOC=________;
(2)若∠BOC=120°,则∠A=_______;
(3)∠A与∠BOC之间具有的数量关系是_______.
9. 已知等腰三角形的一个外角等于100°,则它的底角等于________.
10.将一副直角三角板如图所示放置,使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合,则∠1的度数为________.
11. (2019?贵港二模)如图,∠ACD是△ABC的外角,∠ABC的平分线与∠ACD的平分线交于点A1,∠A1BC的平分线与∠A1CD的平分线交于点A2,…∠An﹣1BC的平行线与∠An﹣1CD的平分线交于点An,设∠A=θ,则∠An= .
12.如图,O是△ABC外一点,OB,OC分别平分△ABC的外角∠CBE,∠BCF.
若∠A=n°,则∠BOC= (用含n的代数式表示).
三、解答题
13.如图,求证:∠A+∠B+∠C+∠D+∠E=180°.
14.(2019春?扬州校级期中)如图①,△ABC的角平分线BD、CE相交于点P.
(1)如果∠A=80°,求∠BPC的度数;
(2)如图②,过P点作直线MN,分别交AB和AC于点M和N,且MN平行于BC,则有∠MPB+∠NPC=90°﹣∠A.若将直线MN绕点P旋转,
(ⅰ)如图③,试探索∠MPB、∠NPC、∠A三者之间的数量关系是否依然成立,并说明理由;
(ⅱ)当直线MN与AB的交点仍在线段AB上,而与AC的交点在AC的延长线上时,如图④,试问(ⅰ)中∠MPB、∠NPC、∠A三者之间的数量关系是否仍然成立?若不成立,请给出∠MPB、∠NPC、∠A三者之间的数量关系,并说明你的理由.
15.如图,在△ABC中,∠ABC的平分线与外角∠ACE的平分线交于点D.试说明.
16.如图所示,在△ABC中,∠1=∠2,∠C>∠B,E为AD上一点,且EF⊥BC于F.
(1)试探索∠DEF与∠B,∠C的大小关系;
(2)如图(2)所示,当点E在AD的延长线上时,其余条件都不变,你在(1)中探索到的结论是否还成立?
【答案与解析】
一、选择题
1. 【答案】A
【解析】(1)由∠A=30°,可得
∠AMN+∠ANM=180°-30°=150°
又∵ ∠CME=∠AMN,∠BNF=∠ANM,
故有∠CME+∠BNF=150°.
2. 【答案】C;
【解析】假如三角形的最小角不小于60°,则必有大于或等于60°的,因为该三角形三个内角互不相等,所以另外两个非最小角一定大于60°,此时,该三角形的三个内角和必大于180°,这与三角形的内角和定理矛盾,故假设不可能成立,即它的最小角必小于60°.
3. 【答案】C ;
【解析】因为三角形的内角中最多有一个钝角,所以外角中最多有一个锐角,即外角中至少有两个钝角.
4. 【答案】B;
【解析】因为三角形的外角和360°,而两个外角的和为270°,所以必有一个外角为90°,所以有一个内有为90°.
5. 【答案】D;
6. 【答案】C;
【解析】解:∵BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,
∵∠ABP=20°,∠ACP=50°,
∴∠ABC=2∠ABP=40°,∠ACM=2∠ACP=100°,
∴∠A=∠ACM﹣∠ABC=60°,
∠ACB=180°﹣∠ACM=80°,
∴∠BCP=∠ACB+∠ACP=130°,
∵∠BPC=20°,
∴∠P=180°﹣∠PBC﹣∠BCP=30°,
∴∠A+∠P=90°,
故选C.
二、填空题
7. 【答案】20°;
【解析】联立方程组: ,解得.
8.【答案】128°, 60°,∠BOC=90°+∠A;
9. 【答案】80°或50°;
【解析】100°的补角为80°,(1)80°为三角形的顶角;(2)80°为三角形底角时,则三角形顶角为20°.
10.【答案】75°;
11.【答案】;
【解析】解:由三角形的外角性质得,∠ACD=∠A+∠ABC,∠A1CD=∠A1+∠A1BC,
∵∠ABC的平分线与∠ACD的平分线交于点A1,
∴∠A1BC=∠ABC,∠A1CD=∠ACD,
∴∠A1+∠A1BC=(∠A+∠ABC)=∠A+∠A1BC,
∴∠A1=∠A,
同理可得∠A2=∠A1==,…,∠An=.
12.【答案】;
【解析】∵∠COB=180-(∠OBC+∠OCB), 而BO,CO分别平分∠CBE,∠BCF, ∴∠OBC=,∠OCB=.
∴∠COB=180°-[]=.
三、解答题
13.【解析】
解:延长BE,交AC于点H,
易得∠BFC=∠A+∠B+∠C
再由∠EFC=∠D+∠E,
上式两边分别相加,得:
∠A+∠B+∠C+∠D+∠E=∠BFC+∠EFC=180°.
即∠A+∠B+∠C+∠D+∠E=180°
14.【解析】
解:(1)如图①∵在△ABC中,∠A+∠B+∠ACB=180°,且∠A=80°,
∴∠ABC+∠ACB=100°,
∵∠1=∠ABC,∠2=∠ACB,
∴∠1+∠2=(∠ABC+∠ACB)=×100°=50°,
∴∠BPC=180°﹣(∠1+∠2)=180°﹣50°=130°.
(2)(ⅰ)如图③,由(1)知:∠BPC=180°﹣(∠1+∠2);
∵∠1+∠2=(180°﹣∠A)=90°∠A,
∴∠BPC=180°﹣(90°﹣∠A)=90°+∠A;
∴∠MPB+∠NPC=180°﹣∠BPC=180°﹣(90°+∠A)=90°﹣∠A.
(ⅱ)不成立,∠MPB﹣∠NPC=90°﹣∠A.
如图④,由(ⅰ)知:∠BPC=90°+∠A,
∴∠MPB﹣∠NPC=180°﹣∠BPC
=180°﹣(90°+∠A)
=90°﹣∠A.
15.【解析】
解:∠D=∠4-∠2=(∠ACE-∠ABC)=∠A,
∴ ∠D=∠A.
16.【解析】
解: (1)∵ ∠1=∠2,∴ ∠1=∠BAC.
又∵ ∠BAC=180°-(∠B+∠C),
∴ ∠1=[180°-(∠B+∠C)]=90°-(∠B+∠C).
∴ ∠EDF=∠B+∠1=∠B+90°-(∠B+∠C)=90°+(∠B-∠C).
又∵ EF⊥BC,∴ ∠EFD=90°.
∴ ∠DEF=90°-∠EDF=90°-[90°+(∠B-∠C)]=(∠C-∠B).
(2)当点E在AD的延长线上时,其余条件都不变,(1)中探索所得的结论仍成立.
【学习目标】
1.理解三角形内角和定理的证明方法;
2.掌握三角形内角和定理及三角形的外角性质;
3.能够运用三角形内角和定理及三角形的外角性质进行相关的计算,证明问题.
与三角形有关的角(提高)巩固练习
【巩固练习】
一、选择题
1.如图所示,一根直尺EF压在三角板30°的角∠BAC上,与两边AC,AB交于M,N.那么∠CME+∠BNF是( )
A.150° B.180° C.135° D.不能确定
2.若一个三角形的三个内角互不相等,则它的最小角必小于( )
A.30° B.45° C.60° D.55°
3.下列语句中,正确的是( )
A.三角形的外角大于任何一个内角
B.三角形的外角等于这个三角形的两个内角之和
C.三角形的外角中,至少有两个钝角
D.三角形的外角中,至少有一个钝角
4.如果一个三角形的两个外角之和为270°,那么这个三角形是 ( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法确定
5.(2019春?泰山区期中)具备下列条件的△ABC中,不是直角三角形的是 ( )
A.∠A+∠B=∠C B.∠A=∠B=∠C
C.∠A:∠B:∠C=1:2:3 D.∠A=2∠B=3∠C
6.(2019春?泰山区期中)如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP=20°,∠ACP=50°,则∠A+∠P=( )
A.70° B.80° C.90° D.100°
二、填空题
7.在△ABC中,若∠A-2∠B=70°,2∠C-∠B=10°,则∠C=________.
8.如图,在△ABC中,∠ABC、∠ACB的平分线相交于点O.
(1)若∠A=76°,则∠BOC=________;
(2)若∠BOC=120°,则∠A=_______;
(3)∠A与∠BOC之间具有的数量关系是_______.
9. 已知等腰三角形的一个外角等于100°,则它的底角等于________.
10.将一副直角三角板如图所示放置,使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合,则∠1的度数为________.
11. (2019?贵港二模)如图,∠ACD是△ABC的外角,∠ABC的平分线与∠ACD的平分线交于点A1,∠A1BC的平分线与∠A1CD的平分线交于点A2,…∠An﹣1BC的平行线与∠An﹣1CD的平分线交于点An,设∠A=θ,则∠An= .
12.如图,O是△ABC外一点,OB,OC分别平分△ABC的外角∠CBE,∠BCF.
若∠A=n°,则∠BOC= (用含n的代数式表示).
三、解答题
13.如图,求证:∠A+∠B+∠C+∠D+∠E=180°.
14.(2019春?扬州校级期中)如图①,△ABC的角平分线BD、CE相交于点P.
(1)如果∠A=80°,求∠BPC的度数;
(2)如图②,过P点作直线MN,分别交AB和AC于点M和N,且MN平行于BC,则有∠MPB+∠NPC=90°﹣∠A.若将直线MN绕点P旋转,
(ⅰ)如图③,试探索∠MPB、∠NPC、∠A三者之间的数量关系是否依然成立,并说明理由;
(ⅱ)当直线MN与AB的交点仍在线段AB上,而与AC的交点在AC的延长线上时,如图④,试问(ⅰ)中∠MPB、∠NPC、∠A三者之间的数量关系是否仍然成立?若不成立,请给出∠MPB、∠NPC、∠A三者之间的数量关系,并说明你的理由.
15.如图,在△ABC中,∠ABC的平分线与外角∠ACE的平分线交于点D.试说明.
16.如图所示,在△ABC中,∠1=∠2,∠C>∠B,E为AD上一点,且EF⊥BC于F.
(1)试探索∠DEF与∠B,∠C的大小关系;
(2)如图(2)所示,当点E在AD的延长线上时,其余条件都不变,你在(1)中探索到的结论是否还成立?
【答案与解析】
一、选择题
1. 【答案】A
【解析】(1)由∠A=30°,可得
∠AMN+∠ANM=180°-30°=150°
又∵ ∠CME=∠AMN,∠BNF=∠ANM,
故有∠CME+∠BNF=150°.
2. 【答案】C;
【解析】假如三角形的最小角不小于60°,则必有大于或等于60°的,因为该三角形三个内角互不相等,所以另外两个非最小角一定大于60°,此时,该三角形的三个内角和必大于180°,这与三角形的内角和定理矛盾,故假设不可能成立,即它的最小角必小于60°.
3. 【答案】C ;
【解析】因为三角形的内角中最多有一个钝角,所以外角中最多有一个锐角,即外角中至少有两个钝角.
4. 【答案】B;
【解析】因为三角形的外角和360°,而两个外角的和为270°,所以必有一个外角为90°,所以有一个内有为90°.
5. 【答案】D;
6. 【答案】C;
【解析】解:∵BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,
∵∠ABP=20°,∠ACP=50°,
∴∠ABC=2∠ABP=40°,∠ACM=2∠ACP=100°,
∴∠A=∠ACM﹣∠ABC=60°,
∠ACB=180°﹣∠ACM=80°,
∴∠BCP=∠ACB+∠ACP=130°,
∵∠BPC=20°,
∴∠P=180°﹣∠PBC﹣∠BCP=30°,
∴∠A+∠P=90°,
故选C.
二、填空题
7. 【答案】20°;
【解析】联立方程组: ,解得.
8.【答案】128°, 60°,∠BOC=90°+∠A;
9. 【答案】80°或50°;
【解析】100°的补角为80°,(1)80°为三角形的顶角;(2)80°为三角形底角时,则三角形顶角为20°.
10.【答案】75°;
11.【答案】;
【解析】解:由三角形的外角性质得,∠ACD=∠A+∠ABC,∠A1CD=∠A1+∠A1BC,
∵∠ABC的平分线与∠ACD的平分线交于点A1,
∴∠A1BC=∠ABC,∠A1CD=∠ACD,
∴∠A1+∠A1BC=(∠A+∠ABC)=∠A+∠A1BC,
∴∠A1=∠A,
同理可得∠A2=∠A1==,…,∠An=.
12.【答案】;
【解析】∵∠COB=180-(∠OBC+∠OCB), 而BO,CO分别平分∠CBE,∠BCF, ∴∠OBC=,∠OCB=.
∴∠COB=180°-[]=.
三、解答题
13.【解析】
解:延长BE,交AC于点H,
易得∠BFC=∠A+∠B+∠C
再由∠EFC=∠D+∠E,
上式两边分别相加,得:
∠A+∠B+∠C+∠D+∠E=∠BFC+∠EFC=180°.
即∠A+∠B+∠C+∠D+∠E=180°
14.【解析】
解:(1)如图①∵在△ABC中,∠A+∠B+∠ACB=180°,且∠A=80°,
∴∠ABC+∠ACB=100°,
∵∠1=∠ABC,∠2=∠ACB,
∴∠1+∠2=(∠ABC+∠ACB)=×100°=50°,
∴∠BPC=180°﹣(∠1+∠2)=180°﹣50°=130°.
(2)(ⅰ)如图③,由(1)知:∠BPC=180°﹣(∠1+∠2);
∵∠1+∠2=(180°﹣∠A)=90°∠A,
∴∠BPC=180°﹣(90°﹣∠A)=90°+∠A;
∴∠MPB+∠NPC=180°﹣∠BPC=180°﹣(90°+∠A)=90°﹣∠A.
(ⅱ)不成立,∠MPB﹣∠NPC=90°﹣∠A.
如图④,由(ⅰ)知:∠BPC=90°+∠A,
∴∠MPB﹣∠NPC=180°﹣∠BPC
=180°﹣(90°+∠A)
=90°﹣∠A.
15.【解析】
解:∠D=∠4-∠2=(∠ACE-∠ABC)=∠A,
∴ ∠D=∠A.
16.【解析】
解: (1)∵ ∠1=∠2,∴ ∠1=∠BAC.
又∵ ∠BAC=180°-(∠B+∠C),
∴ ∠1=[180°-(∠B+∠C)]=90°-(∠B+∠C).
∴ ∠EDF=∠B+∠1=∠B+90°-(∠B+∠C)=90°+(∠B-∠C).
又∵ EF⊥BC,∴ ∠EFD=90°.
∴ ∠DEF=90°-∠EDF=90°-[90°+(∠B-∠C)]=(∠C-∠B).
(2)当点E在AD的延长线上时,其余条件都不变,(1)中探索所得的结论仍成立.
