人教版八年级上数学教学讲义,复习补习资料(巩固练习):06【提高】多边形
文档属性
| 名称 | 人教版八年级上数学教学讲义,复习补习资料(巩固练习):06【提高】多边形 |

|
|
| 格式 | zip | ||
| 文件大小 | 115.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-08 00:00:00 | ||
图片预览


文档简介
多边形(提高)知识讲解
【学习目标】
1.理解多边形的概念;
2.掌握多边形内角和与外角和公式;
3.灵活运用多边形内角和与外角和公式解决有关问题,体验并掌握探索、归纳图形性质的推理方法,进一步培养说理和进行简单推理的能力.
多边形及其内角和(提高)巩固练习
【巩固练习】
一、选择题
1.过一个多边形的一个顶点的所有对角线把多边形分成6个三角形,这个多边形的边数为 ( )
A.5 B.6 C.7 D.8
2.一个多边形的内角和超过640°,则此多边形边数的最小值是 ( )
A.5 B.6 C.7 D.8
3.如果一个多边形的每一个外角都是锐角,那么这个多边形的边数一定不小于 ( )
A.3 B.4 C.5 D.6
4.(2019?莱芜)一个多边形除一个内角外其余内角的和为1510°,则这个多边形对角线的条数是( )
A. 27 B. 35 C. 44 D. 54
5.利用边长相等的正三角形和正六边形的地砖镶嵌地面时,在每个顶点周围有a块正三角形和b块正六边形的地砖(ab≠0),同a+b的值为 ( )
A.3或4 B.4或5 C.5或6 D.4
6.如图所示,已知长方形ABCD,一条直线将该长方形ABCD分割成两个多边形,若这两个多边形的内角和分别为M和N,则M+N不可能是 ( )
/
A.360° B.540° C.720° D.630°
7. (2019?台湾)如图的七边形ABCDEFG中,AB、DE的延长线相交于O点.若图中∠1、∠2、∠3、∠4的外角的角度和为220°,则∠BOD的度数为何?( )
/
A.40 B.45 C.50 D.60
二、填空题
8.一个多边形的内角中,锐角的个数最多有 个.
9.如图,国旗上的五角星的五个角的度数是相同的,每一个角的度数都是 .
/
10.(2019?徐州)若正多边形的一个内角等于140°,则这个正多边形的边数是 .
11.将一块正六边形硬纸片(如图(1)),做成一个底面仍为正六边形且高相等的无盖纸盒(侧面均垂直于底面,如图(2)),需在每一个顶点处剪去一个四边形,如图(1)中的四边形/,那么/的度数是________.
/
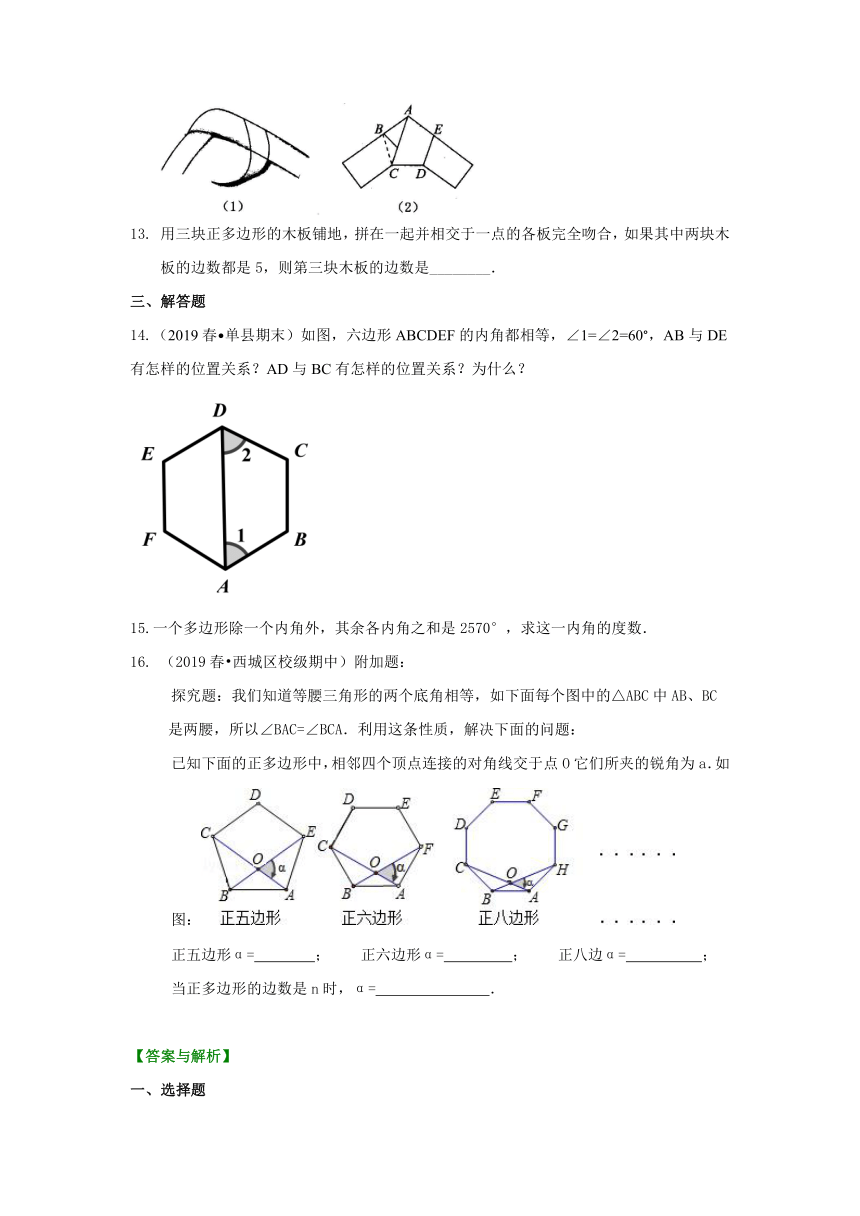
12. 将一个宽度相等且足够长的纸条打一个结,如图(1),然后轻轻拉紧、压平就可以得到如图(2)所示的正五边形ABCDE,其中∠BAC=________.
/
13. 用三块正多边形的木板铺地,拼在一起并相交于一点的各板完全吻合,如果其中两块木板的边数都是5,则第三块木板的边数是________.
三、解答题
14.(2019春?单县期末)如图,六边形ABCDEF的内角都相等,∠1=∠2=60°,AB与DE有怎样的位置关系?AD与BC有怎样的位置关系?为什么?
/
15.一个多边形除一个内角外,其余各内角之和是2570°,求这一内角的度数.
16. (2019春?西城区校级期中)附加题:
探究题:我们知道等腰三角形的两个底角相等,如下面每个图中的△ABC中AB、BC是两腰,所以∠BAC=∠BCA.利用这条性质,解决下面的问题:
已知下面的正多边形中,相邻四个顶点连接的对角线交于点O它们所夹的锐角为a.如图:/
正五边形α= ; 正六边形α= ; 正八边α= ;
当正多边形的边数是n时,α= .
【答案与解析】
一、选择题
1. 【答案】D;
2. 【答案】B;
【解析】(提示:假设内角和是640°的多边形的边数为n,则有(n-2)·180=640,解得/,因为多边形的内角和越大,其边数也越大,故当多边形的内角和超过640°时,其边数/,因为n是正整数,所以其最小值是6.)
3. 【答案】C;
【解析】(提示:因为每个外角都是锐角,即小于90°,设边数为n,则这些锐角的和一定小于n×90°,而外角和为360°,所以360°<n×90°,即n不小于5.)
4. 【答案】C;
【解析】解:设这个内角度数为x,边数为n,
∴(n﹣2)×180°﹣x=1510,
180n=1870+x,
∵n为正整数,
∴n=11,
∴/=44,
故选:C.
5. 【答案】B;
【解析】(提示:根据正多边形镶嵌的条件,在每个顶点处各正多边形的内角之和为360°,得60°·a+120°·b=360°,即a+2b=6,即a=6-2b,因ab≠0,且a,b均为正整数,所以当b=1或2,b=1时,a=4,a+b=5;当b=2时,a=2,a+b=4,故选B.)
6. 【答案】D;
7. 【答案】A;
【解析】解:延长BC交OD与点M,如图所示.
∵多边形的外角和为360°,
∴∠OBC+∠MCD+∠CDM=360°﹣220°=140°.
∵四边形的内角和为360°,
∴∠BOD+∠OBC+180°+∠MCD+∠CDM=360°,
∴∠BOD=40°.
故选A.
二、填空题
8. 【答案】3.
9.【答案】36°;
【解析】将五角星的五个角转移到一个三角形中,由三角形内角和定理以及五角星的各个角都相等,即可求出各个角的度数.
10.【答案】9;
【解析】解:∵正多边形的一个内角是140°,
∴它的外角是:180°﹣140°=40°,
360°÷40°=9.
故答案为:9.
11.【答案】60°;
12.【答案】36°;
13.【答案】10;
三、解答题
14.【解析】
解:AB∥DE,AD∥BC,
∵六边形ABCDEF的内角都相等,
∴六边形ABCDEF的每一个内角都相等120°,
∴∠EDC=∠FAB=120°,
∵∠1=∠2=60°,
∴∠EDA=∠DAB=60°,
∴AB∥DE,
∵∠C=120°,∠2=60°,
∴∠2+∠C=180°,
∴AD∥BC.
15.【解析】
解:设这一内角为x°,多边形的边数为n,则2570°+x°=(n-2)·180°,
/,因为n是正整数,所以x必须等于130.
∴ 这一内角度数为130°;
16.【解析】
解:∵五边形ABCDE是正五边形,
∴AB=BC=AE,∠ABC=∠BAE=108°,
∴∠BEA=∠ACB=/=36°,
∴∠CAE=108°﹣36°=72°,
∴α5=180°﹣∠EAO﹣∠AOE=72°;
同理:α6=60°,α8=45°,
当正多边形的边数是n时,α=/.
【学习目标】
1.理解多边形的概念;
2.掌握多边形内角和与外角和公式;
3.灵活运用多边形内角和与外角和公式解决有关问题,体验并掌握探索、归纳图形性质的推理方法,进一步培养说理和进行简单推理的能力.
多边形及其内角和(提高)巩固练习
【巩固练习】
一、选择题
1.过一个多边形的一个顶点的所有对角线把多边形分成6个三角形,这个多边形的边数为 ( )
A.5 B.6 C.7 D.8
2.一个多边形的内角和超过640°,则此多边形边数的最小值是 ( )
A.5 B.6 C.7 D.8
3.如果一个多边形的每一个外角都是锐角,那么这个多边形的边数一定不小于 ( )
A.3 B.4 C.5 D.6
4.(2019?莱芜)一个多边形除一个内角外其余内角的和为1510°,则这个多边形对角线的条数是( )
A. 27 B. 35 C. 44 D. 54
5.利用边长相等的正三角形和正六边形的地砖镶嵌地面时,在每个顶点周围有a块正三角形和b块正六边形的地砖(ab≠0),同a+b的值为 ( )
A.3或4 B.4或5 C.5或6 D.4
6.如图所示,已知长方形ABCD,一条直线将该长方形ABCD分割成两个多边形,若这两个多边形的内角和分别为M和N,则M+N不可能是 ( )
/
A.360° B.540° C.720° D.630°
7. (2019?台湾)如图的七边形ABCDEFG中,AB、DE的延长线相交于O点.若图中∠1、∠2、∠3、∠4的外角的角度和为220°,则∠BOD的度数为何?( )
/
A.40 B.45 C.50 D.60
二、填空题
8.一个多边形的内角中,锐角的个数最多有 个.
9.如图,国旗上的五角星的五个角的度数是相同的,每一个角的度数都是 .
/
10.(2019?徐州)若正多边形的一个内角等于140°,则这个正多边形的边数是 .
11.将一块正六边形硬纸片(如图(1)),做成一个底面仍为正六边形且高相等的无盖纸盒(侧面均垂直于底面,如图(2)),需在每一个顶点处剪去一个四边形,如图(1)中的四边形/,那么/的度数是________.
/
12. 将一个宽度相等且足够长的纸条打一个结,如图(1),然后轻轻拉紧、压平就可以得到如图(2)所示的正五边形ABCDE,其中∠BAC=________.
/
13. 用三块正多边形的木板铺地,拼在一起并相交于一点的各板完全吻合,如果其中两块木板的边数都是5,则第三块木板的边数是________.
三、解答题
14.(2019春?单县期末)如图,六边形ABCDEF的内角都相等,∠1=∠2=60°,AB与DE有怎样的位置关系?AD与BC有怎样的位置关系?为什么?
/
15.一个多边形除一个内角外,其余各内角之和是2570°,求这一内角的度数.
16. (2019春?西城区校级期中)附加题:
探究题:我们知道等腰三角形的两个底角相等,如下面每个图中的△ABC中AB、BC是两腰,所以∠BAC=∠BCA.利用这条性质,解决下面的问题:
已知下面的正多边形中,相邻四个顶点连接的对角线交于点O它们所夹的锐角为a.如图:/
正五边形α= ; 正六边形α= ; 正八边α= ;
当正多边形的边数是n时,α= .
【答案与解析】
一、选择题
1. 【答案】D;
2. 【答案】B;
【解析】(提示:假设内角和是640°的多边形的边数为n,则有(n-2)·180=640,解得/,因为多边形的内角和越大,其边数也越大,故当多边形的内角和超过640°时,其边数/,因为n是正整数,所以其最小值是6.)
3. 【答案】C;
【解析】(提示:因为每个外角都是锐角,即小于90°,设边数为n,则这些锐角的和一定小于n×90°,而外角和为360°,所以360°<n×90°,即n不小于5.)
4. 【答案】C;
【解析】解:设这个内角度数为x,边数为n,
∴(n﹣2)×180°﹣x=1510,
180n=1870+x,
∵n为正整数,
∴n=11,
∴/=44,
故选:C.
5. 【答案】B;
【解析】(提示:根据正多边形镶嵌的条件,在每个顶点处各正多边形的内角之和为360°,得60°·a+120°·b=360°,即a+2b=6,即a=6-2b,因ab≠0,且a,b均为正整数,所以当b=1或2,b=1时,a=4,a+b=5;当b=2时,a=2,a+b=4,故选B.)
6. 【答案】D;
7. 【答案】A;
【解析】解:延长BC交OD与点M,如图所示.
∵多边形的外角和为360°,
∴∠OBC+∠MCD+∠CDM=360°﹣220°=140°.
∵四边形的内角和为360°,
∴∠BOD+∠OBC+180°+∠MCD+∠CDM=360°,
∴∠BOD=40°.
故选A.
二、填空题
8. 【答案】3.
9.【答案】36°;
【解析】将五角星的五个角转移到一个三角形中,由三角形内角和定理以及五角星的各个角都相等,即可求出各个角的度数.
10.【答案】9;
【解析】解:∵正多边形的一个内角是140°,
∴它的外角是:180°﹣140°=40°,
360°÷40°=9.
故答案为:9.
11.【答案】60°;
12.【答案】36°;
13.【答案】10;
三、解答题
14.【解析】
解:AB∥DE,AD∥BC,
∵六边形ABCDEF的内角都相等,
∴六边形ABCDEF的每一个内角都相等120°,
∴∠EDC=∠FAB=120°,
∵∠1=∠2=60°,
∴∠EDA=∠DAB=60°,
∴AB∥DE,
∵∠C=120°,∠2=60°,
∴∠2+∠C=180°,
∴AD∥BC.
15.【解析】
解:设这一内角为x°,多边形的边数为n,则2570°+x°=(n-2)·180°,
/,因为n是正整数,所以x必须等于130.
∴ 这一内角度数为130°;
16.【解析】
解:∵五边形ABCDE是正五边形,
∴AB=BC=AE,∠ABC=∠BAE=108°,
∴∠BEA=∠ACB=/=36°,
∴∠CAE=108°﹣36°=72°,
∴α5=180°﹣∠EAO﹣∠AOE=72°;
同理:α6=60°,α8=45°,
当正多边形的边数是n时,α=/.
