人教版八年级上数学教学讲义,复习补习资料(巩固练习):12【提高】全等三角形判定一
文档属性
| 名称 | 人教版八年级上数学教学讲义,复习补习资料(巩固练习):12【提高】全等三角形判定一 |  | |
| 格式 | zip | ||
| 文件大小 | 71.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-08 14:16:25 | ||
图片预览

文档简介
全等三角形判定一(SSS,SAS)(提高)
【学习目标】
1.理解和掌握全等三角形判定方法1——“边边边”,和判定方法2——“边角边”;
2.能把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等.
【巩固练习】
一、选择题
1. 如图,已知AB=AC,D为BC的中点,结论:①AD⊥BC;②AD平分∠BAC;③∠B=∠C;④△ABC是等边三角形.其中正确的是( ).
A.①② B. ②③ C. ①②③ D. ③④
/
2.如图,是的中线,、分别是和延长线上的点,且,连接、,下列说法:①;② 和的面积相等;③;④ ≌,其中正确的有( ).
A.1个 B.2个 C.3个 D.4个
/
3. AD为△ABC中BC边上的中线, 若AB=2, AC=4, 则AD的范围是( )
A .AD<6 B. AD>2 C. 2<AD<6 D. 1<AD<3
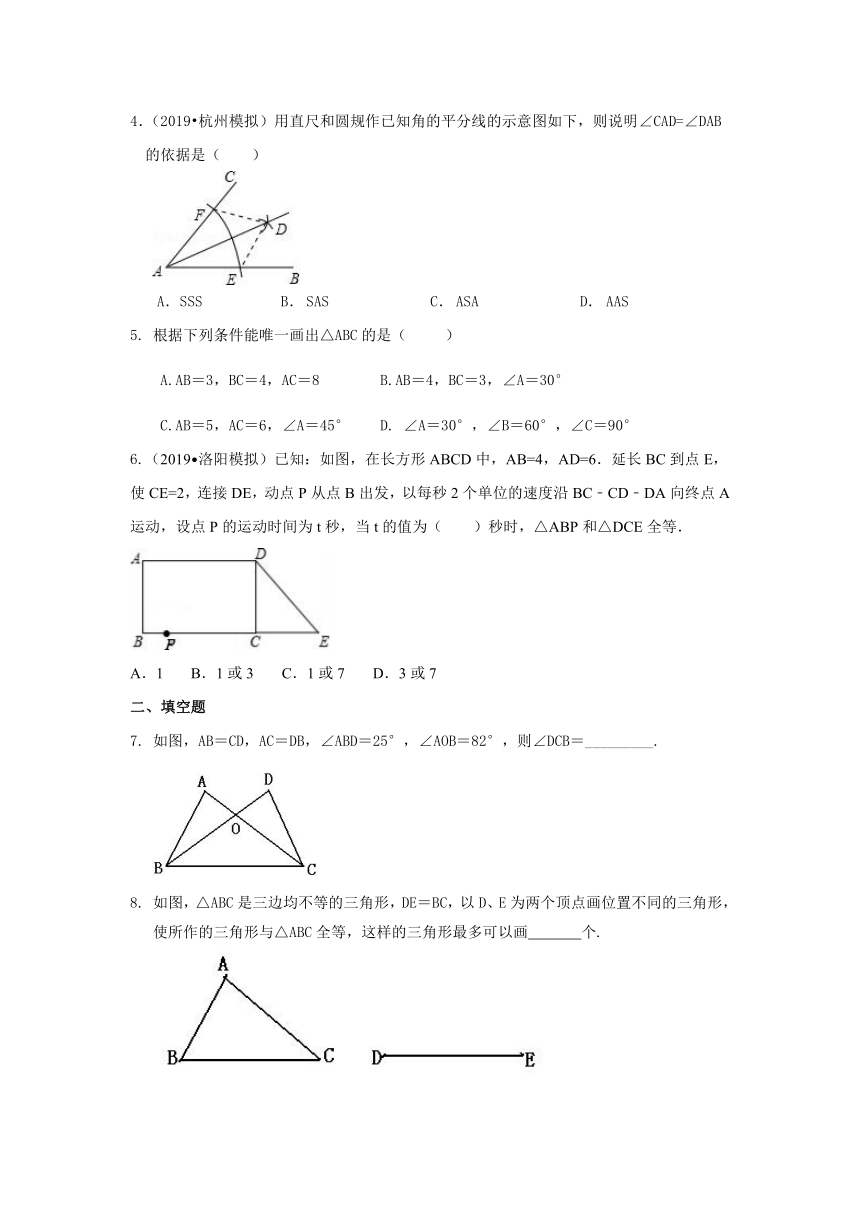
4.(2019?杭州模拟)用直尺和圆规作已知角的平分线的示意图如下,则说明∠CAD=∠DAB的依据是( )
/
A.SSS B. SAS C. ASA D. AAS
5. 根据下列条件能唯一画出△ABC的是( )
A.AB=3,BC=4,AC=8 B.AB=4,BC=3,∠A=30°
C.AB=5,AC=6,∠A=45° D. ∠A=30°,∠B=60°,∠C=90°
6.(2019?洛阳模拟)已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P的运动时间为t秒,当t的值为( )秒时,△ABP和△DCE全等.
/
A.1 B.1或3 C.1或7 D.3或7
二、填空题
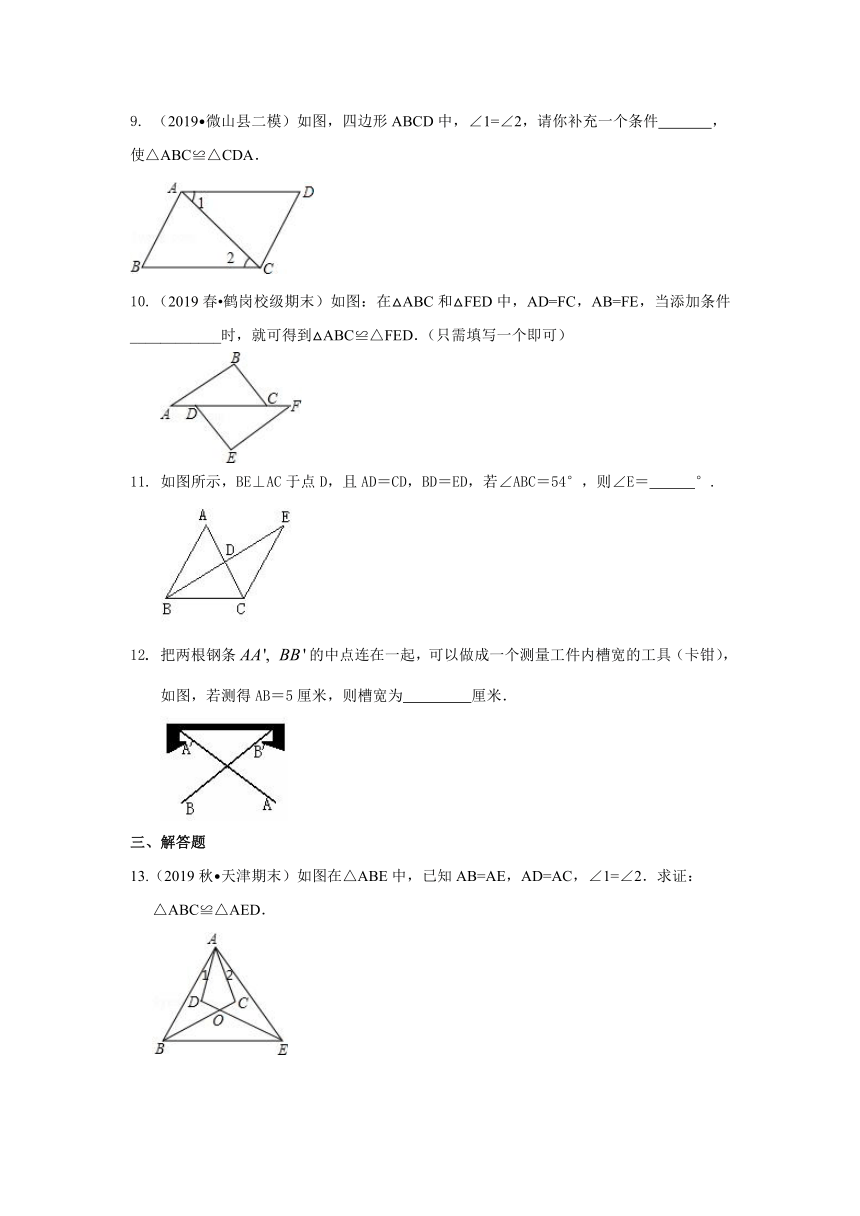
7. 如图,AB=CD,AC=DB,∠ABD=25°,∠AOB=82°,则∠DCB=_________.
/
8. 如图,△ABC是三边均不等的三角形,DE=BC,以D、E为两个顶点画位置不同的三角形,使所作的三角形与△ABC全等,这样的三角形最多可以画 个.
/
9. (2019?微山县二模)如图,四边形ABCD中,∠1=∠2,请你补充一个条件 ,使△ABC≌△CDA.
/
10.(2019春?鹤岗校级期末)如图:在△ABC和△FED中,AD=FC,AB=FE,当添加条件 ____________时,就可得到△ABC≌△FED.(只需填写一个即可)
/
11. 如图所示,BE⊥AC于点D,且AD=CD,BD=ED,若∠ABC=54°,则∠E= °.
/
12. 把两根钢条的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳), 如图,若测得AB=5厘米,则槽宽为 厘米.
/
三、解答题
13.(2019秋?天津期末)如图在△ABE中,已知AB=AE,AD=AC,∠1=∠2.求证:△ABC≌△AED.
/
14. 如图, (B=(C, BD=CE, CD=BF.
求证: (EDF = 90( -(A
/
15. 已知:如图,BE、CF是△ABC的高,且BP=AC,CQ=AB,
求证:AP⊥AQ.
/
【答案与解析】
一.选择题
1. 【答案】C
【解析】由SSS证全等可得①②③是正确的.
2. 【答案】D;
3. 【答案】D;
【解析】用倍长中线法;
4. 【答案】A;
【解析】解:从角平分线的作法得出,
△AFD与△AED的三边全部相等,
则△AFD≌△AED.
故选A.
5. 【答案】C;
【解析】A不能构成三角形,B没有SSA定理,D没有AAA定理.
6. 【答案】C;
【解析】解:因为AB=CD,若∠ABP=∠DCE=90°,BP=CE=2,根据SAS证得△ABP≌△DCE,由题意得:BP=2t=2,所以t=1,
因为AB=CD,若∠BAP=∠DCE=90°,AP=CE=2,根据SAS证得△BAP≌△DCE,
由题意得:AP=16﹣2t=2,解得t=7.所以,当t的值为1或7秒时.△ABP和△DCE全等.
故选C.
二.填空题
7. 【答案】66°;
【解析】可由SSS证明△ABC≌△DCB,∠OBC=∠OCB=,所以∠DCB=
∠ABC=25°+41°=66°
8. 【答案】4;
【解析】在DE的两侧可以各画2个.
9.【答案】AD=BC;
【解析】由题意知,已知条件是△ABC与△CDA对应角∠1=∠2、公共边AC=CA,所以根据全等三角形的判定定理SAS来证△ABC≌△CDA时,需要添加的条件是AD=BC.
10.【答案】BC=ED或∠A=∠F.
11.【答案】27;
【解析】可证△ADB≌△CDB≌△CDE.
12.【答案】5;
三.解答题
13.【解析】
证明:∵∠1=∠2,
∴∠1+∠DAC=∠2+∠DAC,
∴∠BAC=∠EAD,
在△ABC和△AED中,
/,
∴△ABC≌△AED(SAS).
14.【解析】证明:在△ABC中,∠B=∠C,
∴∠B =90((∠A
在△DBF和△ECD中
∴△DBF≌△ECD(SAS)
∴∠BFD=∠CDE
∴∠EDF=180°-∠BDF-∠CDE=180°-(∠BDF+∠BFD)=∠B =90(-∠A .
15.【解析】证明:∵BE⊥AC,CF⊥AB(已知)
∴∠ACF+∠BAC=90°,∠ABE+∠BAC=90°,(三角形内角和定理)
∠ACF=∠ABE(等式性质)
在△ACQ和△PBA中
∵
∴△ACQ≌△PBA(SAS)
∴∠Q=∠BAP(全等三角形对应角相等)
∵CF⊥AB(已知)
∴∠Q+∠QAF=90°,(垂直定义)
∴∠BAP+∠QAF=90°,(等量代换)
∴AP⊥AQ.(垂直定义)
【学习目标】
1.理解和掌握全等三角形判定方法1——“边边边”,和判定方法2——“边角边”;
2.能把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等.
【巩固练习】
一、选择题
1. 如图,已知AB=AC,D为BC的中点,结论:①AD⊥BC;②AD平分∠BAC;③∠B=∠C;④△ABC是等边三角形.其中正确的是( ).
A.①② B. ②③ C. ①②③ D. ③④
/
2.如图,是的中线,、分别是和延长线上的点,且,连接、,下列说法:①;② 和的面积相等;③;④ ≌,其中正确的有( ).
A.1个 B.2个 C.3个 D.4个
/
3. AD为△ABC中BC边上的中线, 若AB=2, AC=4, 则AD的范围是( )
A .AD<6 B. AD>2 C. 2<AD<6 D. 1<AD<3
4.(2019?杭州模拟)用直尺和圆规作已知角的平分线的示意图如下,则说明∠CAD=∠DAB的依据是( )
/
A.SSS B. SAS C. ASA D. AAS
5. 根据下列条件能唯一画出△ABC的是( )
A.AB=3,BC=4,AC=8 B.AB=4,BC=3,∠A=30°
C.AB=5,AC=6,∠A=45° D. ∠A=30°,∠B=60°,∠C=90°
6.(2019?洛阳模拟)已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P的运动时间为t秒,当t的值为( )秒时,△ABP和△DCE全等.
/
A.1 B.1或3 C.1或7 D.3或7
二、填空题
7. 如图,AB=CD,AC=DB,∠ABD=25°,∠AOB=82°,则∠DCB=_________.
/
8. 如图,△ABC是三边均不等的三角形,DE=BC,以D、E为两个顶点画位置不同的三角形,使所作的三角形与△ABC全等,这样的三角形最多可以画 个.
/
9. (2019?微山县二模)如图,四边形ABCD中,∠1=∠2,请你补充一个条件 ,使△ABC≌△CDA.
/
10.(2019春?鹤岗校级期末)如图:在△ABC和△FED中,AD=FC,AB=FE,当添加条件 ____________时,就可得到△ABC≌△FED.(只需填写一个即可)
/
11. 如图所示,BE⊥AC于点D,且AD=CD,BD=ED,若∠ABC=54°,则∠E= °.
/
12. 把两根钢条的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳), 如图,若测得AB=5厘米,则槽宽为 厘米.
/
三、解答题
13.(2019秋?天津期末)如图在△ABE中,已知AB=AE,AD=AC,∠1=∠2.求证:△ABC≌△AED.
/
14. 如图, (B=(C, BD=CE, CD=BF.
求证: (EDF = 90( -(A
/
15. 已知:如图,BE、CF是△ABC的高,且BP=AC,CQ=AB,
求证:AP⊥AQ.
/
【答案与解析】
一.选择题
1. 【答案】C
【解析】由SSS证全等可得①②③是正确的.
2. 【答案】D;
3. 【答案】D;
【解析】用倍长中线法;
4. 【答案】A;
【解析】解:从角平分线的作法得出,
△AFD与△AED的三边全部相等,
则△AFD≌△AED.
故选A.
5. 【答案】C;
【解析】A不能构成三角形,B没有SSA定理,D没有AAA定理.
6. 【答案】C;
【解析】解:因为AB=CD,若∠ABP=∠DCE=90°,BP=CE=2,根据SAS证得△ABP≌△DCE,由题意得:BP=2t=2,所以t=1,
因为AB=CD,若∠BAP=∠DCE=90°,AP=CE=2,根据SAS证得△BAP≌△DCE,
由题意得:AP=16﹣2t=2,解得t=7.所以,当t的值为1或7秒时.△ABP和△DCE全等.
故选C.
二.填空题
7. 【答案】66°;
【解析】可由SSS证明△ABC≌△DCB,∠OBC=∠OCB=,所以∠DCB=
∠ABC=25°+41°=66°
8. 【答案】4;
【解析】在DE的两侧可以各画2个.
9.【答案】AD=BC;
【解析】由题意知,已知条件是△ABC与△CDA对应角∠1=∠2、公共边AC=CA,所以根据全等三角形的判定定理SAS来证△ABC≌△CDA时,需要添加的条件是AD=BC.
10.【答案】BC=ED或∠A=∠F.
11.【答案】27;
【解析】可证△ADB≌△CDB≌△CDE.
12.【答案】5;
三.解答题
13.【解析】
证明:∵∠1=∠2,
∴∠1+∠DAC=∠2+∠DAC,
∴∠BAC=∠EAD,
在△ABC和△AED中,
/,
∴△ABC≌△AED(SAS).
14.【解析】证明:在△ABC中,∠B=∠C,
∴∠B =90((∠A
在△DBF和△ECD中
∴△DBF≌△ECD(SAS)
∴∠BFD=∠CDE
∴∠EDF=180°-∠BDF-∠CDE=180°-(∠BDF+∠BFD)=∠B =90(-∠A .
15.【解析】证明:∵BE⊥AC,CF⊥AB(已知)
∴∠ACF+∠BAC=90°,∠ABE+∠BAC=90°,(三角形内角和定理)
∠ACF=∠ABE(等式性质)
在△ACQ和△PBA中
∵
∴△ACQ≌△PBA(SAS)
∴∠Q=∠BAP(全等三角形对应角相等)
∵CF⊥AB(已知)
∴∠Q+∠QAF=90°,(垂直定义)
∴∠BAP+∠QAF=90°,(等量代换)
∴AP⊥AQ.(垂直定义)
