湘教版九年级数学上册4.2正切课件(19张PPT)
文档属性
| 名称 | 湘教版九年级数学上册4.2正切课件(19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 703.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-10 06:25:57 | ||
图片预览






文档简介
(共19张PPT)
4.2 正切
教学目标
1、理解并掌握正切的含义,能够用tanα表示直角三角形中两边的比值。
2、掌握特殊角的正切值。
3、能够用正切进行简单的计算。
重点: 正切定义的理解以及如何求锐角的正切值.
难点: 正切定义的理解,探索并认识正切.
新课引入
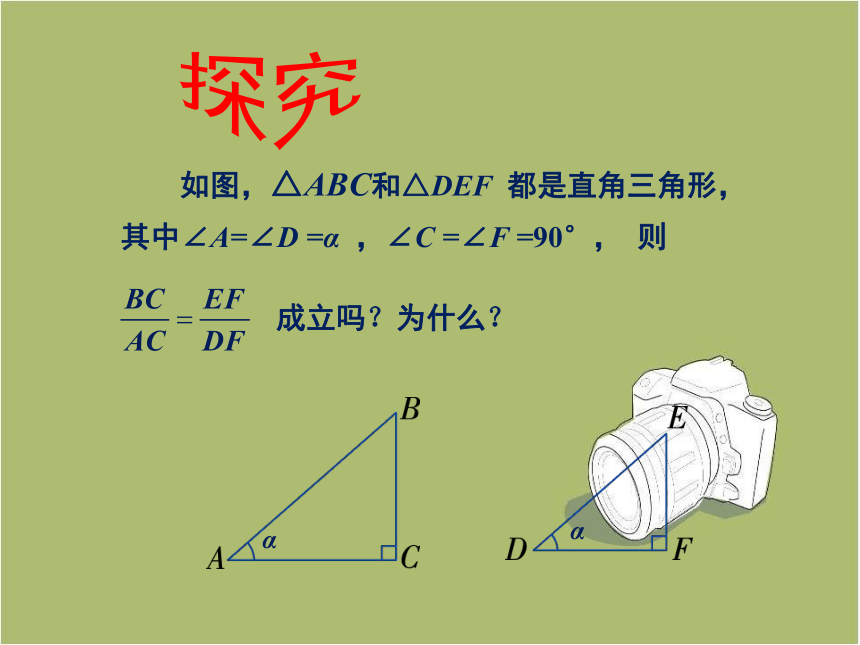
我们已经知道,在直角三角形中,当一个锐角的大小确定时,那么不管这个三角形的大小如何,这个锐角的对边(或邻边)与斜边的比值也就确定(是一个常数). 那么这个锐角的对边与邻边的比值是否也是一个常数呢?
∴ Rt△ABC∽Rt△DEF.
即 BC·DF = AC·EF ,
如下图,在直角三角形中,我们把锐角 的对边与邻边的比叫作角 的正切,记作 , 即
如何求 tan 30°,tan60°的值呢?
从而 AC2=AB2-BC2=(2BC)2-BC2=3BC2.
求tan 45°的值.
现在我们把30°,45°,60°的正弦、余弦、正切值列表归纳如下:
α 30° 45° 60°
sinα
cosα
tanα
如果已知正切值,我们也可以利用计算
器求出它的对应锐角.
对于一般锐角α(30°,45°,60°除外)的正切值,我们也可用计算器来求.
从正弦、余弦、正切的定义看到,任意给定一个锐角 α ,都有唯一确定的比值sinα (或cos α ,tan α )与它对应,并且我们还知道,当锐角α变化时,它的比值sinα(或cosα,tanα)也随之变化. 因此我们把锐角的正弦、余弦和正切统称为角α的锐角三角函数.
例题探究
解:
例 求
课堂练习
1. 在Rt△ABC中,∠C=90°,AC=7,
BC=5,求 tan A,tan B 的值.
(1)1+tan260 ° ;
(2)tan30°cos 30°.
能力提升
2.如图,在矩形ABCD中,E是BC边上的点,AE=BC,DF⊥AE,垂足为点F,连接DE.
(1)求证:AB=DF;
(2)若AD=10,AB=6,求tan∠EDF的值.
解:(1)易证△ABE≌△DFA,∴AB=DF
观察特殊角的三角函数表,发现规律:
通过本小节,你有什么收获?
你还存在哪些疑问,和同伴交流。
4.2 正切
教学目标
1、理解并掌握正切的含义,能够用tanα表示直角三角形中两边的比值。
2、掌握特殊角的正切值。
3、能够用正切进行简单的计算。
重点: 正切定义的理解以及如何求锐角的正切值.
难点: 正切定义的理解,探索并认识正切.
新课引入
我们已经知道,在直角三角形中,当一个锐角的大小确定时,那么不管这个三角形的大小如何,这个锐角的对边(或邻边)与斜边的比值也就确定(是一个常数). 那么这个锐角的对边与邻边的比值是否也是一个常数呢?
∴ Rt△ABC∽Rt△DEF.
即 BC·DF = AC·EF ,
如下图,在直角三角形中,我们把锐角 的对边与邻边的比叫作角 的正切,记作 , 即
如何求 tan 30°,tan60°的值呢?
从而 AC2=AB2-BC2=(2BC)2-BC2=3BC2.
求tan 45°的值.
现在我们把30°,45°,60°的正弦、余弦、正切值列表归纳如下:
α 30° 45° 60°
sinα
cosα
tanα
如果已知正切值,我们也可以利用计算
器求出它的对应锐角.
对于一般锐角α(30°,45°,60°除外)的正切值,我们也可用计算器来求.
从正弦、余弦、正切的定义看到,任意给定一个锐角 α ,都有唯一确定的比值sinα (或cos α ,tan α )与它对应,并且我们还知道,当锐角α变化时,它的比值sinα(或cosα,tanα)也随之变化. 因此我们把锐角的正弦、余弦和正切统称为角α的锐角三角函数.
例题探究
解:
例 求
课堂练习
1. 在Rt△ABC中,∠C=90°,AC=7,
BC=5,求 tan A,tan B 的值.
(1)1+tan260 ° ;
(2)tan30°cos 30°.
能力提升
2.如图,在矩形ABCD中,E是BC边上的点,AE=BC,DF⊥AE,垂足为点F,连接DE.
(1)求证:AB=DF;
(2)若AD=10,AB=6,求tan∠EDF的值.
解:(1)易证△ABE≌△DFA,∴AB=DF
观察特殊角的三角函数表,发现规律:
通过本小节,你有什么收获?
你还存在哪些疑问,和同伴交流。
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
