1.5圆的面积 同步课件

(共50张PPT)
北师大版 六年级上
第一单元 圆的面积
导入

一只马儿被拴在大树的旁边，它围绕大树转了一圈，他很困惑，你能帮马儿解答吗？我们一起看看马儿困惑的是什么。
导入


导入




这根绳子有2米长。
导入





我的最大活动范围是什么呢？
导入


那么聪明的你能为小马解答解惑吗？


































1、了解圆的面积的含义，经历圆面积计算公式的推导过程，掌握圆面积计算公式。
2、能正确运用圆的面积公式计算圆的面积，并能运用圆面积知识解决一些简单实际的问题。
3、在估一估和探究圆面积公式的活动中，体会“化曲为直”的思想，初步感受极限思想。
教学目标
能正确运用圆的面积公式计算圆的面积，并能运用圆面积知识解决一些简单实际的问题。
教学重点
Ⅰ.同步检测
Ⅱ.小白点拨
Ⅳ.课后作业
Ⅲ.课堂检测






































Ⅰ.同步检测






























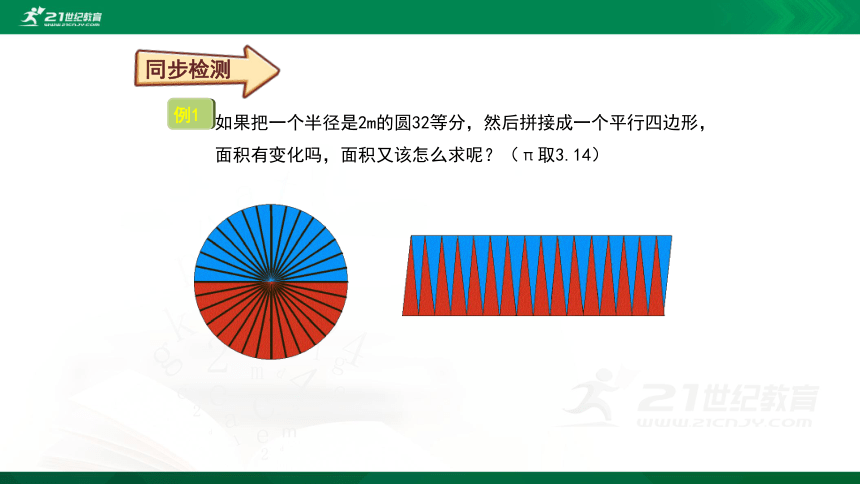
如果把一个半径是2m的圆32等分，然后拼接成一个平行四边形，面积有变化吗，面积又该怎么求呢？（π取3.14）
同步检测


例1
同步检测
【分析】


例1
如果把一个半径是2m的圆32等分，然后拼接成一个平行四边形，面积有变化吗，面积又该怎么求呢？ （π取3.14）
一个平面图形的面积不会随着形状的改变而有所变化，所以这个32等分的圆拼接成的平行四边形的面积没有变化。
平行四边形的面积是底乘以高，底边长度相当于圆的半周长。
同步检测
【分析】


例1
如果把一个半径是2m的圆32等分，然后拼接成一个平行四边形，面积有变化吗，面积又该怎么求呢？ （π取3.14）






低=pr






高= r
平行四边形的面积是底乘以高，高可以近似看成圆的半径。
同步检测
【分析】


例1
如果把一个半径是2m的圆32等分，然后拼接成一个平行四边形，面积有变化吗，面积又该怎么求呢？ （π取3.14）
周长的一半=2πr÷2=πr
圆的面积=平行四边形的面积
=底×高
=πr×r
=πr?
同步检测
【答案】


例1
圆的面积=平行四边形面积
=πr?
=3.14×10?
=314（平方米）
答：圆32等分拼接成平行四边形的面积没有变化，面积是314平方米。
她量出垫子的半径是3厘米，然后沿虚线剪开，伸直以后发现变成了三角形，那三角形的面积是多少呢？（π取3.14）
同步检测


变式





































彬彬妈妈买了好多草绳编成的茶杯垫，彬彬想拿出一个茶杯垫做实验来证明圆的面积。
同步检测


变式
【分析】三角形的底边是茶杯垫的最外一圈的周长，高是是虚线的长度也就是半径。




















r
2 r
π
同步检测


变式
【分析】
圆的面积=三角形的面积
=底×高÷2
=2πr×r÷2
=πr?

圆的面积=三角形面积
=πr?
=3.14×3?
=28.26（平方米）
同步检测


变式
【答案】
圆的面积=三角形面积
=πr?
=3.14×3?
=28.26（平方米）
答：三角形的面积是28.26平方米。


圆的面积可以用三角形或平行四边形的面积推导出来：S=πr?

小白点拨














II.小白点拨

















































































一个圆形花坛的直径是20米，它的占地面积是多少？
经典例题


例1
【答案】
3.14×（20÷2）?=314（平方米）
答：它的占地面积是314平方米。



?

小白点拨
































经典例题
从下面的这张长方形纸上剪下一个最大的圆，这个圆的面积是多少平方厘米?

6Cm
8cm
【答案】
3.14×（6÷2）?=28.26（平方厘米）
答：它的占地面积是28.26平方厘米。


变式

一个圆的直径扩大到原来的2倍，它的面积扩大到原来的（ ）倍。
经典例题


例2
【解析】
我们可以举个例子，如原来圆的直径是4 cm，它的半径就是2 cm，根据面积计算公式可算出面积是3.14×2?=12.56(cm?)；直径扩大到原来的2倍就变成了8 cm，半径就是4 cm，根据面积计算公式可算出面积是3.14×4?=50.24( cm?)。通过比较原来和现在的面积，便可以得出结果。
4


一个圆的半径或直径扩大n倍，这个圆的周长扩大n倍，面积扩大2n倍。

小白点拨





























一个圆的半径扩大到原来的2倍，它的周长扩大（ ）倍，面积扩大到原来的（ ）倍。
经典例题


变式
2
4


例3
经典例题
已知右图中正方形的边长是3厘米，求涂色部分的面积是多少？
【解析】
因为涂色部分是一个不规则的图形，所以不能套公式直接求出它的面积，但我们可以用整个图形的面积减去空白部分的面积来计算。空白部分是一个四分之一圆，半径等于正方形的边长。


例3
经典例题
已知右图中正方形的边长是3厘米，求涂色部分的面积是多少？
【答案】
3×3=9（平方厘米）
3.14×3?÷4=7.065（平方厘米）
9-7.065=1.935（平方厘米）
答：它的占地面积是1.935平方厘米。


计算此类涂色部分是不规则的图形的面积时，通常可以用整个图形的面积减去空白部分的面积。

小白点拨































从一个直径是4cm的圆形纸片上剪下一个最大的正方形，剩下边角料的面积是多少？（π取3.14）
经典例题


变式
【解析】
根据题意可画出左图。圆的面积减去正方形的面积就是边角料的面积。已知圆的直径，利用S=π(d÷2)?可求圆的面积。正方形的对角线是圆的直径，可以把正方形的面积看成是两个三角形的面积之和。两个三角形的底是圆的直径，高是圆的半径，根据公式可求出三角形的面积。

从一个直径是4cm的圆形纸片上剪下一个最大的正方形，剩下边角料的面积是多少？（π取3.14）
经典例题


变式
【答案】
4÷2 =2（平方厘米）
3.14×2?=12.56（平方厘米）
2×2÷2×4=8（平方厘米）
12.56-8=4.56（平方厘米）
答：它的占地面积是4.56平方厘米。


例4
经典例题
下面涂色部分是一个圆环，他的内圆半径是5cm，外圆半径是15cm。它的面积是多少？


例4
经典例题
下面涂色部分是一个圆环，他的内圆半径是5cm，外圆半径是15cm。它的面积是多少？
【答案】
3.14×15?=706.5（平方厘米）
3.14×5?=78.5（平方厘米）
706.5-78.5=628（平方厘米）
答：它的占地面积是628平方厘米。


圆环的面积等于外圆的面积减去内圆的面积，S=π（R?-r?）。

小白点拨





































南山公园中有一个圆形花坛，量得周长是18.84cm，沿着花坛的周围铺上一条大理石小路，小路宽1cm，这条小路的面积是多少？（π取3.14）
经典例题


变式
【答案】
18.84÷3.14÷2=3（米）
3＋1=4（米）
3.14×（4?-3?）=21.98（平方米）
答：这条小路的面积是21.98平方米。
III.课堂检测







































例1
提高训练
先把一个圆沿半径分成若干份，然后拼成一个近似的平行四边形，周长增加了8cm。这个圆的面积是多少？
【答案】
8÷2=4(cm)
3.14×4?=50.24(c·2)
答这个圆的面积是50.24 cm。


例2
提高训练
下图中正方形的面积是30平方厘米，圆的面积是多少平方厘米？
【答案】
3.14×30=94.2(平方厘米)
答：圆的面积是94.2平方厘米。


例3
提高训练
下图中园的周长是16.4cm，园的面积与长方形的面积正好相等。阴影部分的周长是多少厘米？（π值取3.14）
【答案】
16.4÷4=4.1（厘米）
4.1+16.4=20.5（厘米）
答：这条小路的面积是20.5厘米。
学生自评：
教师评价：


1
总 结
掌握圆面积的推导公式


2


3
了解周长面积和圆环公式的区别与联系
根据相关公式学会解决各种类型的圆的应用题
教学建议：师生可根据本次课的综合表现进行打分。


IV.课后作业

1. 判一判。
（1）.圆的半径扩大到原来的2倍，它的面积也随着扩大到原来的2倍。
（ ）
（2）.半圆的面积可以用S=πr?÷2来求。 （ ）
（3）.(易错)半径是2cm的圆，它的周长和面积相等。(π值取3.14)
（ ）
（4）.周长相等的两个圆，它们的面积也一定相等。 （ ）
课后检测
2. 选择。
（1）.周长相等的两个圆的面积( )。
A. 相等 B. 不相等
（2）.(易错)如果一个圆的半径由4 cm。增加到5 cm。，那么它的面积增加( )cm?。
A. π B. 2 π C. 9 π
（3）.一个直径为1 cm的圆与一个边长为1 cm的正方形，它们的面积相比，( )。
A. 圆的面积大 B. 正方形的面积大
C. 一样大 D. 无法比较
课后检测
3. 锦绣大酒店有一张可供40人用餐的大圆桌，直径是10m，做一张这样的大圆桌的桌面至少需要多少平方米的材料？（π至值取3.14）
课后检测

?
课后检测
5. 一个运动场跑道的形状与大小如下图所示。这个跑道的两边是半圆形，中间是长方形，这个运动场的占面积是多少？
课后检测

?
课后检测
谢谢
21世纪教育网（www.21cnjy.com) 中小学教育资源网站
有大把高质量资料？一线教师？一线教研员？
欢迎加入21世纪教育网教师合作团队！！月薪过万不是梦！！
详情请看：
https://www.21cnjy.com/help/help_extract.php