沪教版(五四学制)八上:18.2 正比例函数(3) 课件(16张PPT)
文档属性
| 名称 | 沪教版(五四学制)八上:18.2 正比例函数(3) 课件(16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 335.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-10 00:00:00 | ||
图片预览






文档简介
课件16张PPT。18.2(3)正比例函数的性质3、用”描点法”画函数图像的步骤:
(1)______(2)______(3)______
4、正比例函数的图像是__________复习回顾概念图像列表描点连线一条直线1、解析式形如__________的函数叫做
正比例函数
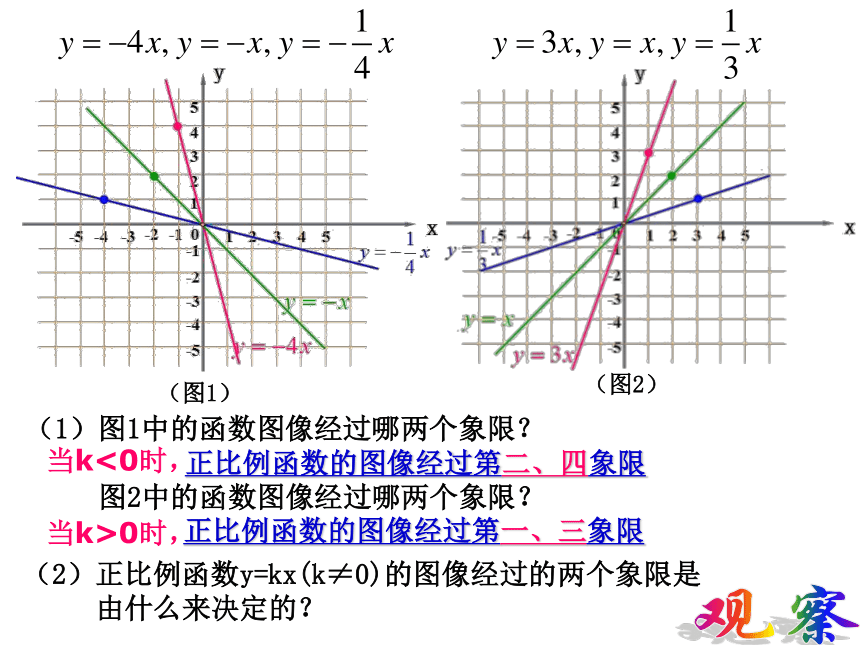
2、正比例函数的定义域是___________y=kx(k≠0)一切实数操作在同一直角坐标平面内,分别画出下列函数的图像: 概念图像性质(1)图1中的函数图像经过哪两个象限?
正比例函数的图像经过第二、四象限
图2中的函数图像经过哪两个象限?
正比例函数的图像经过第一、三象限(2)正比例函数y=kx(k≠0)的图像经过的两个象限是
由什么来决定的?观察当k>0时,当k<0时,
(图2)(3)当k>0时,一条直线上的点的横坐标从小到大逐渐变化时,
点的位置随着从_____到 逐渐变化(填“高”或“低”);
当k>0时,自变量x的值逐渐 时,y的值也随着逐渐________
(填“增大”或“减小”).低高增大增大减小减小-6-3036(3)当k<0时,一条直线上的点的横坐标从小到大逐渐变化时,
点的位置随着从_____到 逐渐变化(填“高”或“低”);
当k<0时,自变量x的值逐渐 时,y的值则随着逐渐________
(填“增大”或“减小”).高低减小
(图1)增大减小增大概括 正比例函数的性质:
(1)当k>0时,正比例函数的图像经过第一,三象限;
自变量x的值逐渐增大时,y的值也随着逐渐增大.
(2)当k<0时,正比例函数的图像经过第二,四象限;
自变量x的值逐渐增大时,y的值则随着逐渐减小.巩固练习一、三增大<减小>一、三例题1:已知正比例函数y=(1-2a)x,如果y的值随x的值增大而减小,那么a的取值范围是什么?例题讲解巩固练习二、四a>4例题2:在水管放水的过程中,放水的时间x(分)与流出的水量y(立方米)是两个变量.已知水管每分钟流出的水量是0.2立方米,放水的过程持续10分钟,写出y与x之间的函数解析式,并指出函数的定义域,再画出这个函数的图像.解:由题意得: 函数解析式是 y=0.2x
函数的定义域是 0≤x≤10.
例题讲解4. 正方形ABCD的边长为6,P是边BC上一点,BP的长为x(cm)与△ABP的面积S(cm2)是两个变量.写出S与x之间的函数解析式,并指出函数的定义域,再画出这个函数的图像.提高课堂小结1、正比例函数的性质;函数正比例函数k符号图像经过象限增减性经过第一、三象限经过第二、四象限课堂小结 正比例函数的性质:课堂小结1、正比例函数的性质;
2、函数学习中常用的思想方法;
3、学习后体会.作业布置1、拓展:
(1)在同一直角坐标平面内,画正比例函数y=5x和y=-5x的图像;
(2)观察(1)所画的两个函数图像,它们关于x轴对称吗?关于y轴对称吗?
(3)由此你得到什么结论?
2、校本作业:习题18.2(3) 讨论在解决正比例函数实际应用问题时,应注意什么呢? 在实际问题中,两个变量y和x成正比例时,设x为自变量,比例系数为k,那么y是x的函数,这个函数的解析式是y=kx.但是,此时函数的定义域一般是部分实数,函数的图像一般就是直线的一部分(还可能只是在一条直线上的一些点).象这样的函数,我们对它进行研究时,可以把它看作正比例函数,但要特别注意它的定义域.
(1)______(2)______(3)______
4、正比例函数的图像是__________复习回顾概念图像列表描点连线一条直线1、解析式形如__________的函数叫做
正比例函数
2、正比例函数的定义域是___________y=kx(k≠0)一切实数操作在同一直角坐标平面内,分别画出下列函数的图像: 概念图像性质(1)图1中的函数图像经过哪两个象限?
正比例函数的图像经过第二、四象限
图2中的函数图像经过哪两个象限?
正比例函数的图像经过第一、三象限(2)正比例函数y=kx(k≠0)的图像经过的两个象限是
由什么来决定的?观察当k>0时,当k<0时,
(图2)(3)当k>0时,一条直线上的点的横坐标从小到大逐渐变化时,
点的位置随着从_____到 逐渐变化(填“高”或“低”);
当k>0时,自变量x的值逐渐 时,y的值也随着逐渐________
(填“增大”或“减小”).低高增大增大减小减小-6-3036(3)当k<0时,一条直线上的点的横坐标从小到大逐渐变化时,
点的位置随着从_____到 逐渐变化(填“高”或“低”);
当k<0时,自变量x的值逐渐 时,y的值则随着逐渐________
(填“增大”或“减小”).高低减小
(图1)增大减小增大概括 正比例函数的性质:
(1)当k>0时,正比例函数的图像经过第一,三象限;
自变量x的值逐渐增大时,y的值也随着逐渐增大.
(2)当k<0时,正比例函数的图像经过第二,四象限;
自变量x的值逐渐增大时,y的值则随着逐渐减小.巩固练习一、三增大<减小>一、三例题1:已知正比例函数y=(1-2a)x,如果y的值随x的值增大而减小,那么a的取值范围是什么?例题讲解巩固练习二、四a>4例题2:在水管放水的过程中,放水的时间x(分)与流出的水量y(立方米)是两个变量.已知水管每分钟流出的水量是0.2立方米,放水的过程持续10分钟,写出y与x之间的函数解析式,并指出函数的定义域,再画出这个函数的图像.解:由题意得: 函数解析式是 y=0.2x
函数的定义域是 0≤x≤10.
例题讲解4. 正方形ABCD的边长为6,P是边BC上一点,BP的长为x(cm)与△ABP的面积S(cm2)是两个变量.写出S与x之间的函数解析式,并指出函数的定义域,再画出这个函数的图像.提高课堂小结1、正比例函数的性质;函数正比例函数k符号图像经过象限增减性经过第一、三象限经过第二、四象限课堂小结 正比例函数的性质:课堂小结1、正比例函数的性质;
2、函数学习中常用的思想方法;
3、学习后体会.作业布置1、拓展:
(1)在同一直角坐标平面内,画正比例函数y=5x和y=-5x的图像;
(2)观察(1)所画的两个函数图像,它们关于x轴对称吗?关于y轴对称吗?
(3)由此你得到什么结论?
2、校本作业:习题18.2(3) 讨论在解决正比例函数实际应用问题时,应注意什么呢? 在实际问题中,两个变量y和x成正比例时,设x为自变量,比例系数为k,那么y是x的函数,这个函数的解析式是y=kx.但是,此时函数的定义域一般是部分实数,函数的图像一般就是直线的一部分(还可能只是在一条直线上的一些点).象这样的函数,我们对它进行研究时,可以把它看作正比例函数,但要特别注意它的定义域.
