沪教版(五四学制)八年级上册第十九章 几何证明:19.1 命题和证明(1) 课件(共22张PPT)
文档属性
| 名称 | 沪教版(五四学制)八年级上册第十九章 几何证明:19.1 命题和证明(1) 课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 484.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-10 10:57:44 | ||
图片预览





文档简介
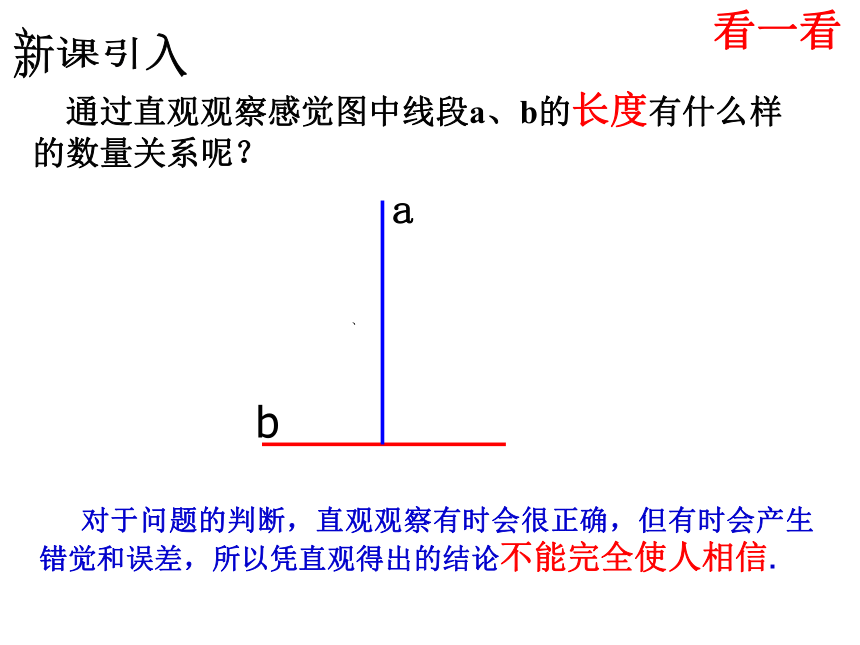
课件22张PPT。19.1命题和证明(1)——演绎证明新课引入b 通过直观观察感觉图中线段a、b的长度有什么样
的数量关系呢?、 对于问题的判断,直观观察有时会很正确,但有时会产生错觉和误差,所以凭直观得出的结论不能完全使人相信.看一看 一般来说,证明是指人们为获得使人信服的结论所采用的手段,有“实践证明”、“历史证明”、“举例证明”等多种形式;而对数学结论的正确性进行证明,还有更为严格的形式. 怎样才算严格的数学证明呢?
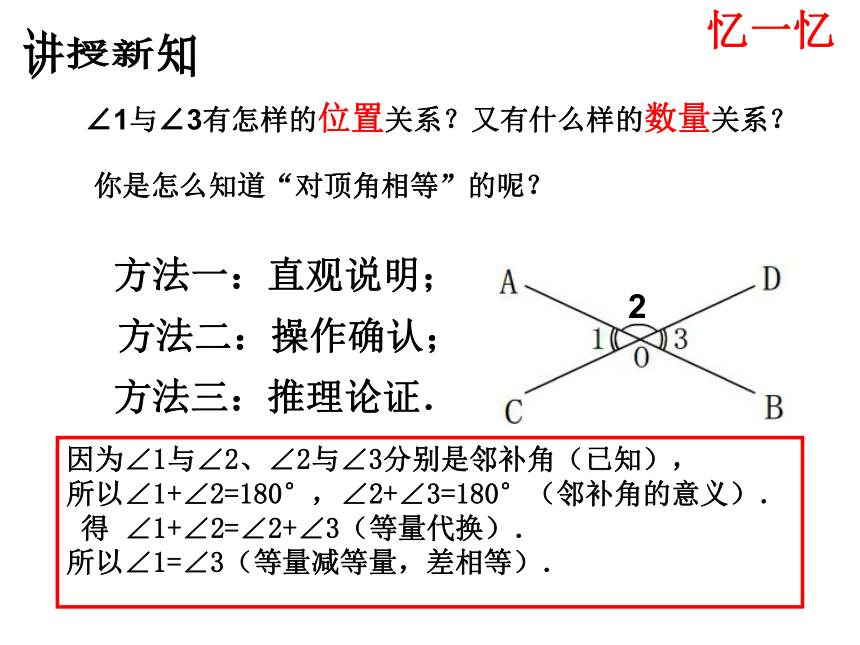
下面我们以“对顶角相等”为例进行分析. 我们常用什么样的方式让人们相信你说的话是真的,你做的事是正确的呢?方法一:直观说明; ? ? ?方法二:操作确认;方法三:推理论证. 因为∠1与∠2、∠2与∠3分别是邻补角(已知),
所以∠1+∠2=180°,∠2+∠3=180°(邻补角的意义).
得 ∠1+∠2=∠2+∠3(等量代换).
所以∠1=∠3(等量减等量,差相等).讲授新知忆一忆∠1与∠3有怎样的位置关系?又有什么样的数量关系?你是怎么知道“对顶角相等”的呢?2 像上述第三种方法,我们运用演绎推理的方法得到“对顶角相等”这个结论,演绎推理的过程就是演绎证明. 演绎证明:从已知的概念、条件出发,依据已被确认的事实和公认的逻辑规则,推导出某结论为正确的过程. 这三种方法中,哪一种最可靠,最有说服力? 演绎证明这种方法不仅是在几何中使用,在代数中也用到演绎推理.辩一辩演绎证明这种方法是由古希腊数学家欧几里得在公元前300年整
理编写的《Elements》一书中所采用的,这部数学名著被广泛
地认为是历史上最成功的教科书之一,该书前6卷在公元1607年
由我国明代科学家徐光启(上海徐家汇人)和意大利传教士利玛
窦合作译成中文,定名为《几何原本》,传入我国,后9卷由清朝
著名数学家李善兰于1856年在上海墨海书馆翻译完成. 演绎推理是数学证明的一种常用的、完全可靠的方
法.演绎证明是一种严格的数学证明.
在本书中,演绎证明简称证明. 学习演绎证明可以使我们的思维严格、缜密,其表
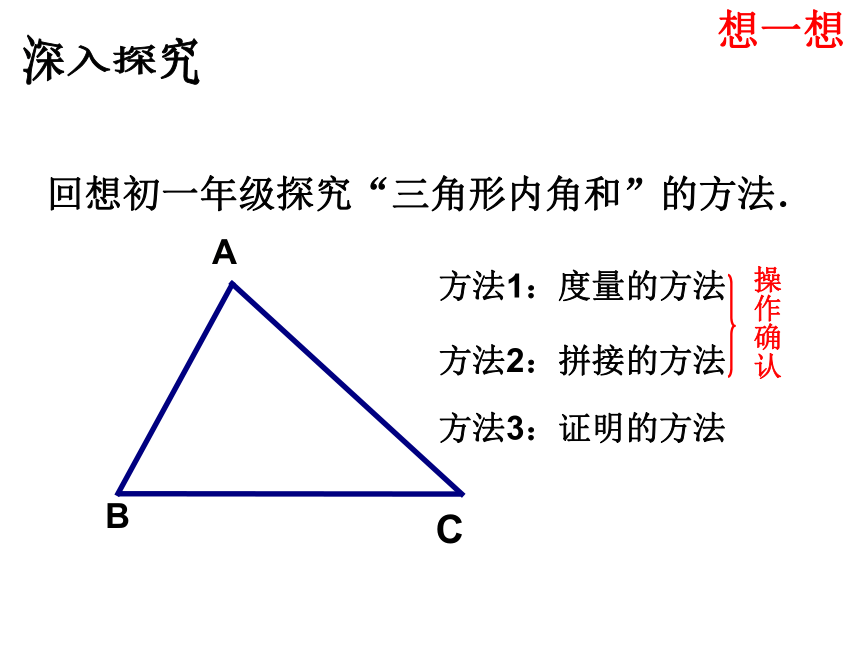
达条理清楚、无可辩驳 . ‖深入探究回想初一年级探究“三角形内角和”的方法.方法1:度量的方法方法2:拼接的方法想一想方法3:证明的方法方法2:拼接法.
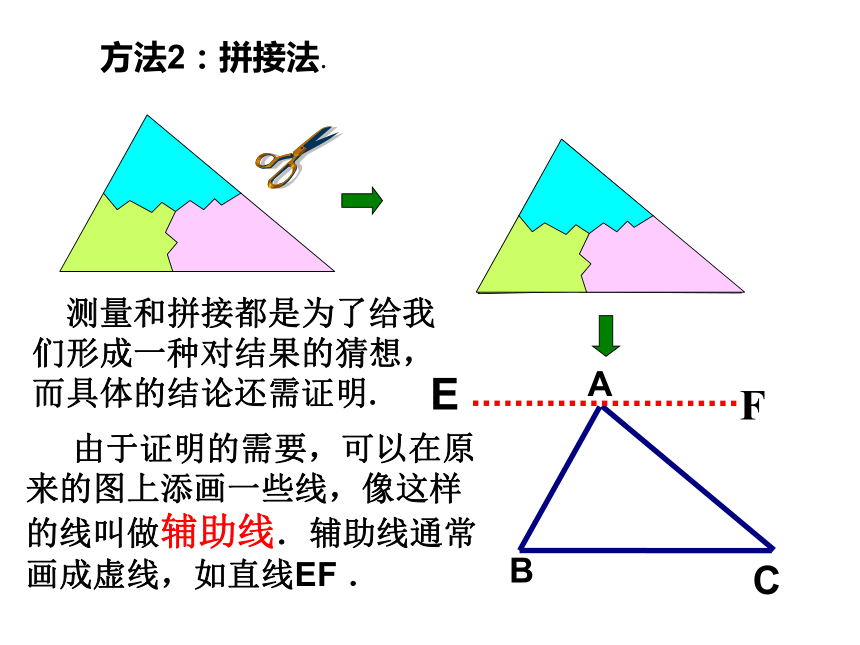
测量和拼接都是为了给我们形成一种对结果的猜想,而具体的结论还需证明. 由于证明的需要,可以在原来的图上添画一些线,像这样的线叫做辅助线.辅助线通常画成虚线,如直线EF .过△ABC的顶点A作直线EF∥BC.
因为EF∥BC(所作),
所以∠EAB=∠B,∠FAC=∠C(两直线平行,内错角相等) .
因为E、A、F在直线EF上(所作),
所以∠EAB+∠BAC+∠FAC=180°(平角的意义).
所以∠B+∠BAC+∠C=180°(等量代换).
根据猜想,把三角形的3个内角的和转化成一个平角. 严格的证明固然重要,但是结论的发现往往离不开归纳、猜想,所以直观观察、实验操作和演绎证明往往有互补作用. 通过上述问题,我们可以看到演绎证明的每一步推理都必须有依据(依据可以是已知条件和已证事项,或者已有的概念、性质等),通常把每一步的依据写在由其得到的结论后面的括号内. 下面我们以,“对顶角相等”的证明为例研究段与段之间的因果关系 . 证明是由若干个推理段落组成,即有多层因果关系,
从整体上看,前一段中的果为后一段提供了因,一连串
这样连贯、有序的因果关系组成了完整的证明. 因为∠1与∠2、∠2与∠3分别是邻补角(已知),
所以∠1+∠2=180°,∠2+∠3=180°(邻补角的意义).
得∠1+∠2=∠2+∠3(等量代换).
所以∠1=∠3(等量减等量,差相等).第一段因果关系:
因:“∠1与∠2、∠2与∠3分别是邻补角”;
果:“∠1+∠2=180°,∠2+∠3=180°”
“依据”是“邻补角的意义” . 第二段因果关系:
因:“∠1+∠2=180°,∠2+∠3=180°”;
果:“∠1+∠2=∠2+∠3”;“依据”是“等量代换”. 第三段因果关系:
因:“∠1+∠2=∠2+∠3”;
果:“∠1=∠3”;“依据”是“等量减等量,差相等”.说一说 再尝试说一说“三角形内角和”证明过程中的因果关系. 注意:寻找因果关系可以从条件出发找到由条件能够直接得到的结果,也可以从结论出发去寻找得到这个结论所需要的条件,同时还要注意导致这个结果的原因往往不止一个,需要从前面的段落中去寻找.新知巩固1.已知:如图,BE平分∠ABC,BD=DE,求证:DE∥BC.
证明:因为 BE平分∠ABC(已知);
所以 ∠1=∠2(角平分线的意义).
因为 BD=DE(已知) ;
所以 ∠2=∠3(等边对等角);
所以 ∠1=∠3(等量代换);
所以 DE∥BC(内错角相等,两直线平行).其中,因:
果:∠1=∠2.
因:
果:∠2=∠3.
因:
果:∠1=∠3.
因:∠1=∠3;
果: BE平分∠ABCBD=DE∠1=∠2, ∠2=∠3 证明过程由以下6句话组成,请根据几何的因果关系和逻辑关系将它们重新排列先后顺序.⑥因为 BD=DE④所以 ∠1=∠2②因为 BE平分∠ABC①所以 ∠1=∠3③所以 ∠2=∠3⑤所以 DE∥BC理一理DE∥BC.②④⑥③①⑤⑥③②④①⑤2.已知:如图,BE平分∠ABC, DE∥BC ,求证: BD=DE .
请先完成证明过程,再写出其中的因果关系.写一写
因为 BE平分∠ABC(已知 );所以 ∠1=∠2(角平分线的意义).因为 DE∥BC (已知);所以 ∠1=∠3 (两直线平行,内错角相等);所以 ∠2=∠3 (等量代换);所以 BD=DE (等角对等边).证明:
其中,因:
果:
因:
果:
因:
果:
因:
果:BE平分∠ABC∠1=∠2DE∥BC∠1=∠2 ,∠1=∠3∠2=∠3BD=DE∠2=∠3∠1=∠3经过本节课的学习,你有哪些收获?归纳小结1.知道了什么叫证明,明白了几何学习中演绎证明的重要性;
2.知道了如何进行推理和表达;3.学会了根据证明过程去写对应的因果关系.作业布置
1.必做题:练习册19.1(1)第1题.
2.选做题:回顾“等腰三角形性质——等边对等角”的说明过程,
并尝试证明,再指出证明过程中的因果关系.谢 谢!一因一果一因多果多因一果多因多果已知:如图,点D、E、F分别在△ABC的边BC、AB、AC上,且DF∥AB,DE∥AC,试证明: .
.
证明:
①因为DF∥AB(已知),
②所以∠B=∠FDC(两直线平行,同位角相等),
③ ∠BED=∠EDF (两直线平行,内错角相等) .
④因为DE∥AC(已知),
⑤所以∠C=∠EDB (两直线平行,同位角相等),
⑥ ∠A=∠BED (两直线平行,同位角相等),
⑦得 ∠EDF=∠A (等量代换) .
⑧因为点D在△ABC的边BC上(已知),
⑨所以∠FDC+ ∠EDF+ ∠EDB=1800 (平角的意义),
⑩所以∠A+ ∠B+ ∠C=1800 (等量代换) .
(说说上述证明过程中的因果关系)
★★▲▲■■■试一试2.已知:如图,BE平分∠ABC, DE∥BC ,求证: BD=DE .
请先完成证明过程,再写出其中的因果关系.写一写
因为 BE平分∠ABC(已知 );所以 ∠1=∠2(角平分线的意义).因为 DE∥BC (已知);所以 ∠1=∠3 (两直线平行,内错角相等);所以 ∠2=∠3 (等量代换);所以 BD=DE (等角对等边).证明:
其中,因:
果:
因:
果:
因:
果:
因:
果:BE平分∠ABC∠1=∠2DE∥BC∠1=∠2 ,∠1=∠3∠2=∠3BD=DE∠2=∠3∠1=∠3
的数量关系呢?、 对于问题的判断,直观观察有时会很正确,但有时会产生错觉和误差,所以凭直观得出的结论不能完全使人相信.看一看 一般来说,证明是指人们为获得使人信服的结论所采用的手段,有“实践证明”、“历史证明”、“举例证明”等多种形式;而对数学结论的正确性进行证明,还有更为严格的形式. 怎样才算严格的数学证明呢?
下面我们以“对顶角相等”为例进行分析. 我们常用什么样的方式让人们相信你说的话是真的,你做的事是正确的呢?方法一:直观说明; ? ? ?方法二:操作确认;方法三:推理论证. 因为∠1与∠2、∠2与∠3分别是邻补角(已知),
所以∠1+∠2=180°,∠2+∠3=180°(邻补角的意义).
得 ∠1+∠2=∠2+∠3(等量代换).
所以∠1=∠3(等量减等量,差相等).讲授新知忆一忆∠1与∠3有怎样的位置关系?又有什么样的数量关系?你是怎么知道“对顶角相等”的呢?2 像上述第三种方法,我们运用演绎推理的方法得到“对顶角相等”这个结论,演绎推理的过程就是演绎证明. 演绎证明:从已知的概念、条件出发,依据已被确认的事实和公认的逻辑规则,推导出某结论为正确的过程. 这三种方法中,哪一种最可靠,最有说服力? 演绎证明这种方法不仅是在几何中使用,在代数中也用到演绎推理.辩一辩演绎证明这种方法是由古希腊数学家欧几里得在公元前300年整
理编写的《Elements》一书中所采用的,这部数学名著被广泛
地认为是历史上最成功的教科书之一,该书前6卷在公元1607年
由我国明代科学家徐光启(上海徐家汇人)和意大利传教士利玛
窦合作译成中文,定名为《几何原本》,传入我国,后9卷由清朝
著名数学家李善兰于1856年在上海墨海书馆翻译完成. 演绎推理是数学证明的一种常用的、完全可靠的方
法.演绎证明是一种严格的数学证明.
在本书中,演绎证明简称证明. 学习演绎证明可以使我们的思维严格、缜密,其表
达条理清楚、无可辩驳 . ‖深入探究回想初一年级探究“三角形内角和”的方法.方法1:度量的方法方法2:拼接的方法想一想方法3:证明的方法方法2:拼接法.
测量和拼接都是为了给我们形成一种对结果的猜想,而具体的结论还需证明. 由于证明的需要,可以在原来的图上添画一些线,像这样的线叫做辅助线.辅助线通常画成虚线,如直线EF .过△ABC的顶点A作直线EF∥BC.
因为EF∥BC(所作),
所以∠EAB=∠B,∠FAC=∠C(两直线平行,内错角相等) .
因为E、A、F在直线EF上(所作),
所以∠EAB+∠BAC+∠FAC=180°(平角的意义).
所以∠B+∠BAC+∠C=180°(等量代换).
根据猜想,把三角形的3个内角的和转化成一个平角. 严格的证明固然重要,但是结论的发现往往离不开归纳、猜想,所以直观观察、实验操作和演绎证明往往有互补作用. 通过上述问题,我们可以看到演绎证明的每一步推理都必须有依据(依据可以是已知条件和已证事项,或者已有的概念、性质等),通常把每一步的依据写在由其得到的结论后面的括号内. 下面我们以,“对顶角相等”的证明为例研究段与段之间的因果关系 . 证明是由若干个推理段落组成,即有多层因果关系,
从整体上看,前一段中的果为后一段提供了因,一连串
这样连贯、有序的因果关系组成了完整的证明. 因为∠1与∠2、∠2与∠3分别是邻补角(已知),
所以∠1+∠2=180°,∠2+∠3=180°(邻补角的意义).
得∠1+∠2=∠2+∠3(等量代换).
所以∠1=∠3(等量减等量,差相等).第一段因果关系:
因:“∠1与∠2、∠2与∠3分别是邻补角”;
果:“∠1+∠2=180°,∠2+∠3=180°”
“依据”是“邻补角的意义” . 第二段因果关系:
因:“∠1+∠2=180°,∠2+∠3=180°”;
果:“∠1+∠2=∠2+∠3”;“依据”是“等量代换”. 第三段因果关系:
因:“∠1+∠2=∠2+∠3”;
果:“∠1=∠3”;“依据”是“等量减等量,差相等”.说一说 再尝试说一说“三角形内角和”证明过程中的因果关系. 注意:寻找因果关系可以从条件出发找到由条件能够直接得到的结果,也可以从结论出发去寻找得到这个结论所需要的条件,同时还要注意导致这个结果的原因往往不止一个,需要从前面的段落中去寻找.新知巩固1.已知:如图,BE平分∠ABC,BD=DE,求证:DE∥BC.
证明:因为 BE平分∠ABC(已知);
所以 ∠1=∠2(角平分线的意义).
因为 BD=DE(已知) ;
所以 ∠2=∠3(等边对等角);
所以 ∠1=∠3(等量代换);
所以 DE∥BC(内错角相等,两直线平行).其中,因:
果:∠1=∠2.
因:
果:∠2=∠3.
因:
果:∠1=∠3.
因:∠1=∠3;
果: BE平分∠ABCBD=DE∠1=∠2, ∠2=∠3 证明过程由以下6句话组成,请根据几何的因果关系和逻辑关系将它们重新排列先后顺序.⑥因为 BD=DE④所以 ∠1=∠2②因为 BE平分∠ABC①所以 ∠1=∠3③所以 ∠2=∠3⑤所以 DE∥BC理一理DE∥BC.②④⑥③①⑤⑥③②④①⑤2.已知:如图,BE平分∠ABC, DE∥BC ,求证: BD=DE .
请先完成证明过程,再写出其中的因果关系.写一写
因为 BE平分∠ABC(已知 );所以 ∠1=∠2(角平分线的意义).因为 DE∥BC (已知);所以 ∠1=∠3 (两直线平行,内错角相等);所以 ∠2=∠3 (等量代换);所以 BD=DE (等角对等边).证明:
其中,因:
果:
因:
果:
因:
果:
因:
果:BE平分∠ABC∠1=∠2DE∥BC∠1=∠2 ,∠1=∠3∠2=∠3BD=DE∠2=∠3∠1=∠3经过本节课的学习,你有哪些收获?归纳小结1.知道了什么叫证明,明白了几何学习中演绎证明的重要性;
2.知道了如何进行推理和表达;3.学会了根据证明过程去写对应的因果关系.作业布置
1.必做题:练习册19.1(1)第1题.
2.选做题:回顾“等腰三角形性质——等边对等角”的说明过程,
并尝试证明,再指出证明过程中的因果关系.谢 谢!一因一果一因多果多因一果多因多果已知:如图,点D、E、F分别在△ABC的边BC、AB、AC上,且DF∥AB,DE∥AC,试证明: .
.
证明:
①因为DF∥AB(已知),
②所以∠B=∠FDC(两直线平行,同位角相等),
③ ∠BED=∠EDF (两直线平行,内错角相等) .
④因为DE∥AC(已知),
⑤所以∠C=∠EDB (两直线平行,同位角相等),
⑥ ∠A=∠BED (两直线平行,同位角相等),
⑦得 ∠EDF=∠A (等量代换) .
⑧因为点D在△ABC的边BC上(已知),
⑨所以∠FDC+ ∠EDF+ ∠EDB=1800 (平角的意义),
⑩所以∠A+ ∠B+ ∠C=1800 (等量代换) .
(说说上述证明过程中的因果关系)
★★▲▲■■■试一试2.已知:如图,BE平分∠ABC, DE∥BC ,求证: BD=DE .
请先完成证明过程,再写出其中的因果关系.写一写
因为 BE平分∠ABC(已知 );所以 ∠1=∠2(角平分线的意义).因为 DE∥BC (已知);所以 ∠1=∠3 (两直线平行,内错角相等);所以 ∠2=∠3 (等量代换);所以 BD=DE (等角对等边).证明:
其中,因:
果:
因:
果:
因:
果:
因:
果:BE平分∠ABC∠1=∠2DE∥BC∠1=∠2 ,∠1=∠3∠2=∠3BD=DE∠2=∠3∠1=∠3
