沪教版(五四学制)八年级上册第十九章几何证明:19.2 证明举例(第1课时) 课件(18张PPT)
文档属性
| 名称 | 沪教版(五四学制)八年级上册第十九章几何证明:19.2 证明举例(第1课时) 课件(18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 139.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-09 17:09:33 | ||
图片预览




文档简介
课件18张PPT。19.2 证明举例(1) ——有关两直线平行… …复习旧知
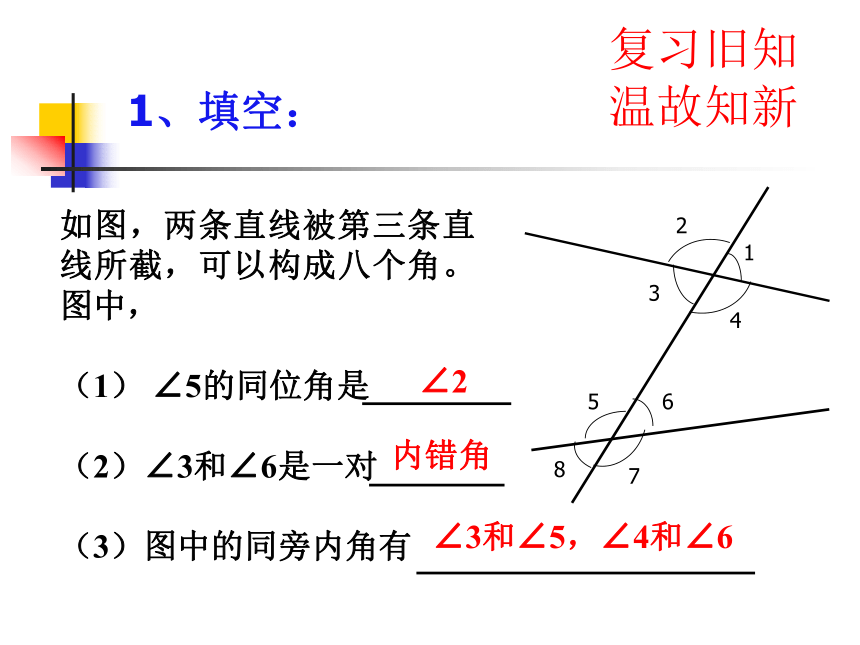
温故知新12345678如图,两条直线被第三条直线所截,可以构成八个角。图中,
(1) ∠5的同位角是
(2)∠3和∠6是一对
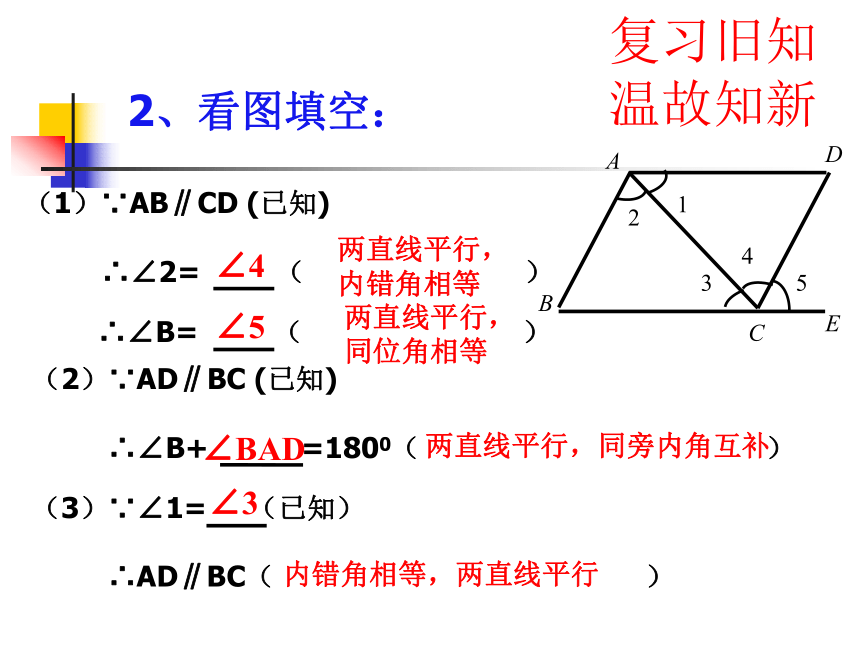
(3)图中的同旁内角有1、填空:内错角∠2∠3和∠5,∠4和∠6复习旧知 温故知新2、看图填空:BCADE14532 ∴∠B= ( )
(2)∵AD∥BC (已知)
∴∠B+ =1800( )(3)∵∠1= (已知)
∴AD∥BC( ) ∠4两直线平行,内错角相等∠5两直线平行,同位角相等∠BAD两直线平行,同旁内角互补∠3内错角相等,两直线平行复习旧知 温故知新(4)∵∠B+ =1800(已知)
∴AB∥CD( )BCADE14532(5)∵∠5= (已知)
∴AB∥CD( )∠BCD同旁内角互补,两直线平行∠B同位角相等,两直线平行复习旧知 温故知新如图, ∵ a∥b,b∥c(已知)
∴ ∥ ( ) 3、填空:abc想一想:依据学过的哪些方法可以证明两条直线平行?ab平行于同一条直线的两条直线也平行 平行线的判定定理:
(1)同位角相等,两直线平行;
(2)内错角相等,两直线平行;
(3)同旁内角互补,两直线平行;平行线的传递性:平行于同一条直线的两条
直线也平行;
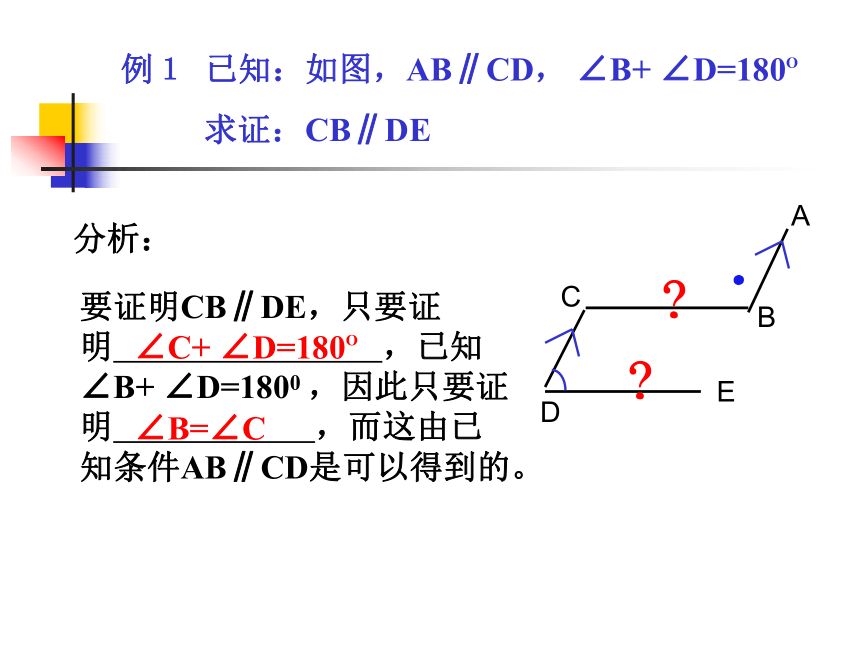
例1 已知:如图,AB∥CD, ∠B+ ∠D=180O
求证:CB∥DE分析:要证明CB∥DE,只要证
明 ,已知
∠B+ ∠D=1800 ,因此只要证
明 ,而这由已知条件AB∥CD是可以得到的。 ∠C+ ∠D=180O∠B=∠C.﹖﹖例1变式练习:
已知:如图, CB∥DE , ∠B+ ∠D=180O
求证: AB∥CD要证明AB ∥ CD,只要证
明 ,已知
∠B+ ∠D=1800 ,因此只要证
明 ,而这由已知条件CB∥DE是可以得到的。 分析:﹖﹖.∠B=∠C∠C+ ∠D=180O例2 已知:如图,点D,E,F分别是AC、AB、BC 上的点,DF∥AB, ∠DFE=∠A
求证:EF∥ACABCEDF要证明EF ∥AC,只要证明
又已知∠DFE=∠A ,因此只要证明 ,而这由已知条件DF∥AB得到的。 分析:﹖﹖∠A=∠BEF∠DFE=∠BEF例2 已知:如图,点D,E,F分别是AC、AB、BC 上的点,DF∥AB, ∠DFE=∠A
求证:EF∥ACABCEDF要证明EF ∥AC,只要证明
又已知∠DFE=∠A ,因此只要证明 ,而这由已知条件DF∥AB得到的。 分析:﹖﹖∠DFE=∠FDC∠A=∠FDC例2 已知:如图,点D,E,F分别是AC、AB、BC 上的点,DF∥AB, ∠DFE=∠A
求证:EF∥ACABCEDF要证明EF ∥AC,只要证明
又已知∠DFE=∠A ,因此只要证明 ,
而这由已知条件DF∥AB得到的。 分析:﹖﹖∠A+∠AEF=1800∠DFE+∠AEF=1800例2变式练习:
已知:如图,DF∥AB, EF∥AC
求证: ∠DFE=∠AABCEDF﹖﹖练习练习1 已知:如图,∠1=∠B, ∠2=∠D
求证:AB∥CDCFDEBA12练习2 已知:如图,∠C=∠1, ∠B=∠D
求证:AB∥DFADFBEC12课堂小结通过本节课的学习,你有哪些收获和体会…深化学习 已知:如图,AB∥CD,直线EF分别与AB、
CD相交于点G、H,
(1) 若GP、HN分别平分∠BGF、∠DHF,
求证:GP∥HNACBDGEFHPN21(2) 若GP、HN分别平分∠BGF、∠CHE,
探索:GP、HN具有怎样的位置关系?
(3) 若GP、HN分别平分∠BGF、∠EHD,
探索:GP、HN具有怎样的位置关系?必做题:练习册 习题19.2(1)
选做题:提高题课后作业
(1) ∠5的同位角是
(2)∠3和∠6是一对
(3)图中的同旁内角有1、填空:内错角∠2∠3和∠5,∠4和∠6复习旧知 温故知新2、看图填空:BCADE14532 ∴∠B= ( )
(2)∵AD∥BC (已知)
∴∠B+ =1800( )(3)∵∠1= (已知)
∴AD∥BC( ) ∠4两直线平行,内错角相等∠5两直线平行,同位角相等∠BAD两直线平行,同旁内角互补∠3内错角相等,两直线平行复习旧知 温故知新(4)∵∠B+ =1800(已知)
∴AB∥CD( )BCADE14532(5)∵∠5= (已知)
∴AB∥CD( )∠BCD同旁内角互补,两直线平行∠B同位角相等,两直线平行复习旧知 温故知新如图, ∵ a∥b,b∥c(已知)
∴ ∥ ( ) 3、填空:abc想一想:依据学过的哪些方法可以证明两条直线平行?ab平行于同一条直线的两条直线也平行 平行线的判定定理:
(1)同位角相等,两直线平行;
(2)内错角相等,两直线平行;
(3)同旁内角互补,两直线平行;平行线的传递性:平行于同一条直线的两条
直线也平行;
例1 已知:如图,AB∥CD, ∠B+ ∠D=180O
求证:CB∥DE分析:要证明CB∥DE,只要证
明 ,已知
∠B+ ∠D=1800 ,因此只要证
明 ,而这由已知条件AB∥CD是可以得到的。 ∠C+ ∠D=180O∠B=∠C.﹖﹖例1变式练习:
已知:如图, CB∥DE , ∠B+ ∠D=180O
求证: AB∥CD要证明AB ∥ CD,只要证
明 ,已知
∠B+ ∠D=1800 ,因此只要证
明 ,而这由已知条件CB∥DE是可以得到的。 分析:﹖﹖.∠B=∠C∠C+ ∠D=180O例2 已知:如图,点D,E,F分别是AC、AB、BC 上的点,DF∥AB, ∠DFE=∠A
求证:EF∥ACABCEDF要证明EF ∥AC,只要证明
又已知∠DFE=∠A ,因此只要证明 ,而这由已知条件DF∥AB得到的。 分析:﹖﹖∠A=∠BEF∠DFE=∠BEF例2 已知:如图,点D,E,F分别是AC、AB、BC 上的点,DF∥AB, ∠DFE=∠A
求证:EF∥ACABCEDF要证明EF ∥AC,只要证明
又已知∠DFE=∠A ,因此只要证明 ,而这由已知条件DF∥AB得到的。 分析:﹖﹖∠DFE=∠FDC∠A=∠FDC例2 已知:如图,点D,E,F分别是AC、AB、BC 上的点,DF∥AB, ∠DFE=∠A
求证:EF∥ACABCEDF要证明EF ∥AC,只要证明
又已知∠DFE=∠A ,因此只要证明 ,
而这由已知条件DF∥AB得到的。 分析:﹖﹖∠A+∠AEF=1800∠DFE+∠AEF=1800例2变式练习:
已知:如图,DF∥AB, EF∥AC
求证: ∠DFE=∠AABCEDF﹖﹖练习练习1 已知:如图,∠1=∠B, ∠2=∠D
求证:AB∥CDCFDEBA12练习2 已知:如图,∠C=∠1, ∠B=∠D
求证:AB∥DFADFBEC12课堂小结通过本节课的学习,你有哪些收获和体会…深化学习 已知:如图,AB∥CD,直线EF分别与AB、
CD相交于点G、H,
(1) 若GP、HN分别平分∠BGF、∠DHF,
求证:GP∥HNACBDGEFHPN21(2) 若GP、HN分别平分∠BGF、∠CHE,
探索:GP、HN具有怎样的位置关系?
(3) 若GP、HN分别平分∠BGF、∠EHD,
探索:GP、HN具有怎样的位置关系?必做题:练习册 习题19.2(1)
选做题:提高题课后作业
