沪教版(五四学制)八年级上册第十九章几何证明:19.2 证明举例(第2课时) 课件(共13张PPT)
文档属性
| 名称 | 沪教版(五四学制)八年级上册第十九章几何证明:19.2 证明举例(第2课时) 课件(共13张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 394.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-09 17:12:14 | ||
图片预览




文档简介
课件13张PPT。证明举例(2)复习:1、三角形的边、角的有关性质:
三角形的边的性质:三角形任意两边之和大于第三边;任意两边之差小于第三边。
三角形的角的性质:
内角和性质:三角形的内角和为180度。
外角性质:1)三角形的一个外角等于与它不相邻的两个内角的和。
2) 三角形的一个外角大于任何一个与它不相邻的内角。
复习:2、全等三角形判定方法:(S、S、S);(S、A、S);(A、S、A);(A、A、S); 全等三角形的性质: 全等三角形对应边相等;
全等三角形对应角相等。3、等腰三角形判定:等角对等边
等腰三角形性质:等边对等角。
等腰三角形的三线合一。
4、等边三角形的判定:
1)三条边都相等的三角形是等边三角形。
2)三个内角都相等的三角形是等边三角形.
3)有一个角等于60 °的等腰三角形是等边三角形。
等边三角形的性质:
等边三角形的三条边都相等,三个内角都等于60 ° 。
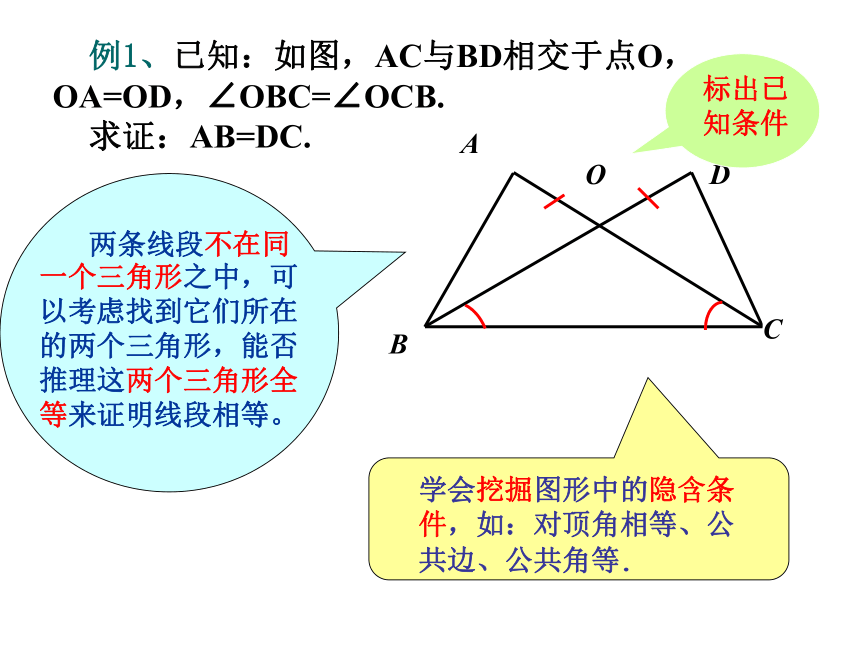
例1、已知:如图,AC与BD相交于点O,OA=OD,∠OBC=∠OCB.
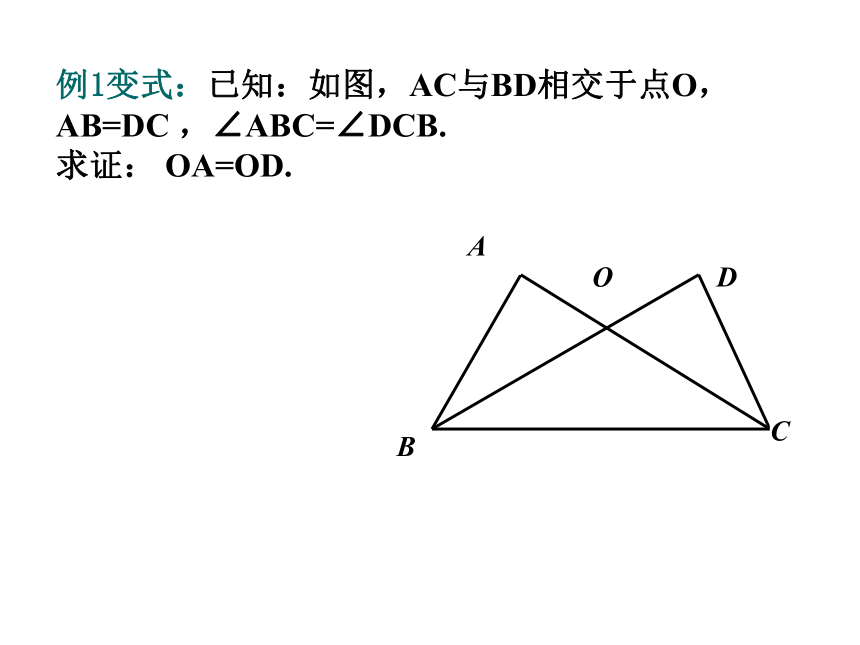
求证:AB=DC. 两条线段不在同一个三角形之中,可以考虑找到它们所在的两个三角形,能否推理这两个三角形全等来证明线段相等。学会挖掘图形中的隐含条件,如:对顶角相等、公共边、公共角等. 例1变式:已知:如图,AC与BD相交于点O, AB=DC ,∠ABC=∠DCB.
求证: OA=OD. 例2、 已知:如图,AB=AC,DB=DC.
求证:∠B=∠C.例2变式(1):图形变换成如图,能否证明? 例2变式(1): 已知:如图,AB=AC,DB=DC.
求证:∠B=∠C.例2变式(2): 把条件AB=AC与∠B=∠C对调能否证明?例2变式(2):
已知:如图, ∠B=∠C ,DB=DC.
求证: AB=AC.练习:1、已知:如图所示,点D、E在BC上,AB=AC,AD=AE.
求证:BD=CE.2、已知:如图,AB=AC,E是AC上任意一点,ED⊥BC,垂足为D,延长DE交BA的延长线于点F.
求证:AE=AF.3、已知:如图,AB=AD,BE=DE,C是AE延长线上一点.
求证:∠BCA=∠DCA. 谈谈你在这节课上学到了哪些证明线段或角相等的常用方法?课堂小结:
三角形的边的性质:三角形任意两边之和大于第三边;任意两边之差小于第三边。
三角形的角的性质:
内角和性质:三角形的内角和为180度。
外角性质:1)三角形的一个外角等于与它不相邻的两个内角的和。
2) 三角形的一个外角大于任何一个与它不相邻的内角。
复习:2、全等三角形判定方法:(S、S、S);(S、A、S);(A、S、A);(A、A、S); 全等三角形的性质: 全等三角形对应边相等;
全等三角形对应角相等。3、等腰三角形判定:等角对等边
等腰三角形性质:等边对等角。
等腰三角形的三线合一。
4、等边三角形的判定:
1)三条边都相等的三角形是等边三角形。
2)三个内角都相等的三角形是等边三角形.
3)有一个角等于60 °的等腰三角形是等边三角形。
等边三角形的性质:
等边三角形的三条边都相等,三个内角都等于60 ° 。
例1、已知:如图,AC与BD相交于点O,OA=OD,∠OBC=∠OCB.
求证:AB=DC. 两条线段不在同一个三角形之中,可以考虑找到它们所在的两个三角形,能否推理这两个三角形全等来证明线段相等。学会挖掘图形中的隐含条件,如:对顶角相等、公共边、公共角等. 例1变式:已知:如图,AC与BD相交于点O, AB=DC ,∠ABC=∠DCB.
求证: OA=OD. 例2、 已知:如图,AB=AC,DB=DC.
求证:∠B=∠C.例2变式(1):图形变换成如图,能否证明? 例2变式(1): 已知:如图,AB=AC,DB=DC.
求证:∠B=∠C.例2变式(2): 把条件AB=AC与∠B=∠C对调能否证明?例2变式(2):
已知:如图, ∠B=∠C ,DB=DC.
求证: AB=AC.练习:1、已知:如图所示,点D、E在BC上,AB=AC,AD=AE.
求证:BD=CE.2、已知:如图,AB=AC,E是AC上任意一点,ED⊥BC,垂足为D,延长DE交BA的延长线于点F.
求证:AE=AF.3、已知:如图,AB=AD,BE=DE,C是AE延长线上一点.
求证:∠BCA=∠DCA. 谈谈你在这节课上学到了哪些证明线段或角相等的常用方法?课堂小结:
