沪教版(五四学制)八年级上册第十九章几何证明:19.4 线段的垂直平分线 课件(共16张PPT)
文档属性
| 名称 | 沪教版(五四学制)八年级上册第十九章几何证明:19.4 线段的垂直平分线 课件(共16张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 500.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-10 00:00:00 | ||
图片预览


文档简介
课件16张PPT。学会总结学会验证学会猜想学会运用19.4线段的垂直平分线驶向胜利的彼岸(2)线段AB的垂直平分线上的点C、E、P到A、B 两
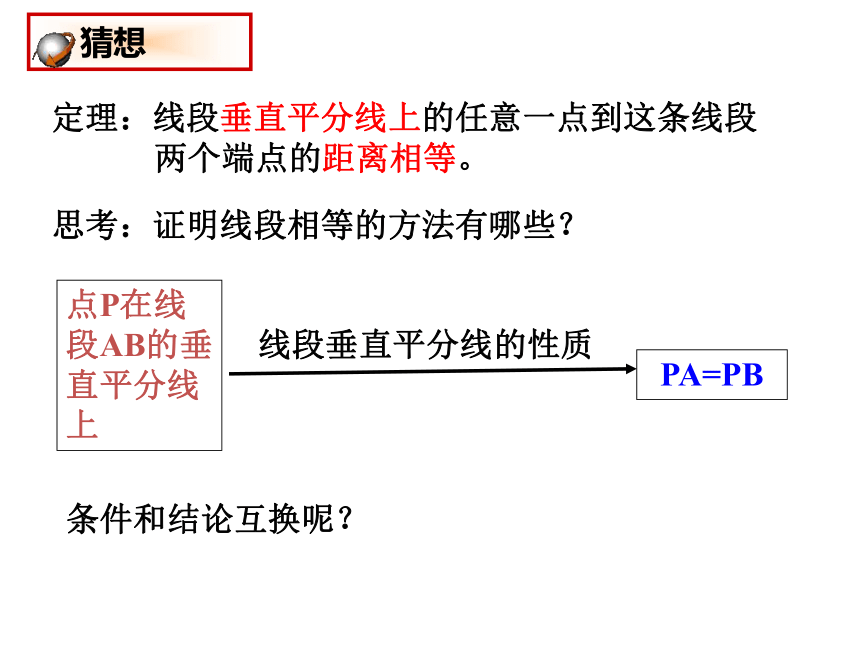
点的距离相等吗?(1)等腰 ABC(其CA=CB)是轴对称图形,其对称轴是? 猜想ABCDPE猜测1:线段垂直平分线上的任意一点到这条线段两个
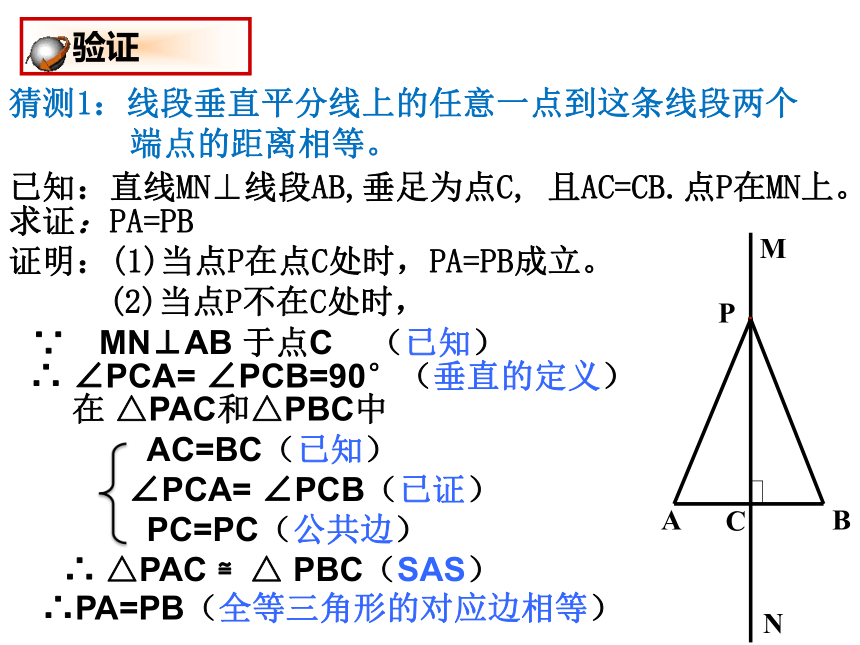
端点的距离相等。已知:直线MN⊥线段AB,垂足为点C, 且AC=CB.点P在MN上。
求证:PA=PBPC 验证证明:(1)当点P在点C处时,PA=PB成立。∵ MN⊥AB 于点C (已知)∴ ∠PCA= ∠PCB=90°(垂直的定义) 在 △PAC和△PBC中
AC=BC(已知)
∠PCA= ∠PCB(已证)
PC=PC(公共边)
∴ △PAC ≌△ PBC(SAS)∴PA=PB(全等三角形的对应边相等) (2)当点P不在C处时,线段垂直平分线的性质:线段垂直平分线上的任意一点 到这条线段两个端点的距离相等。几何语言:∵点P在线段AB的垂直平分线上(已知)∴PA=PB
(线段垂直平分线上的任意一点到这条线段两个端点的距离相等。 )
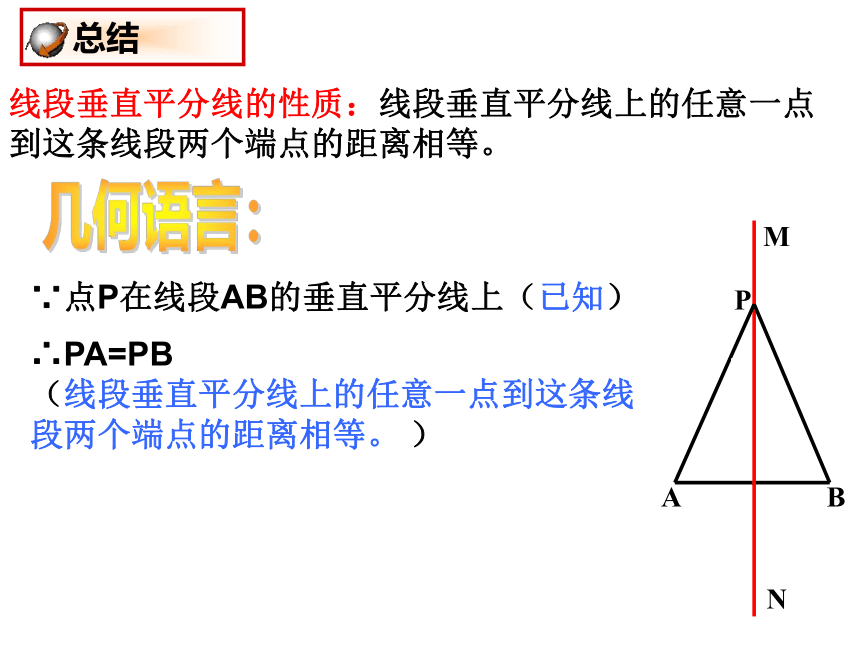
总结定理:线段垂直平分线上的任意一点到这条线段
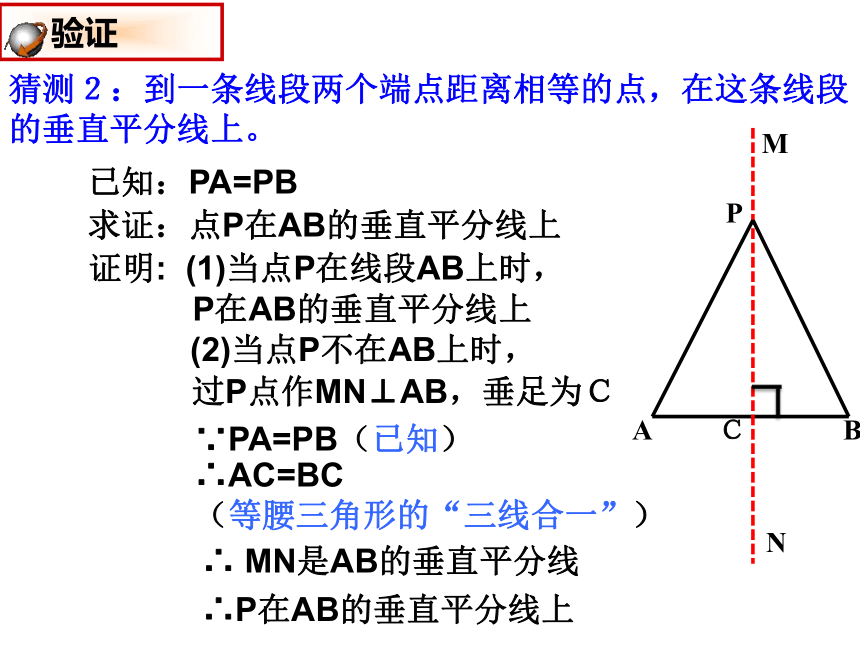
两个端点的距离相等。PA=PB点P在线段AB的垂直平分线上条件和结论互换呢?思考:证明线段相等的方法有哪些?线段垂直平分线的性质 猜想猜测2:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上。已知:PA=PB求证:点P在AB的垂直平分线上证明: (1)当点P在线段AB上时,∵PA=PB(已知)∴AC=BC
(等腰三角形的“三线合一”)ABPC∴ MN是AB的垂直平分线∴P在AB的垂直平分线上
验证P在AB的垂直平分线上(2)当点P不在AB上时,过P点作MN⊥AB,垂足为C∵ PA=PB(已知) ∴点P在线段AB的垂直平分线上
(和一条线段两个端点距离相等的点,
在这条线段的垂直平分线上)
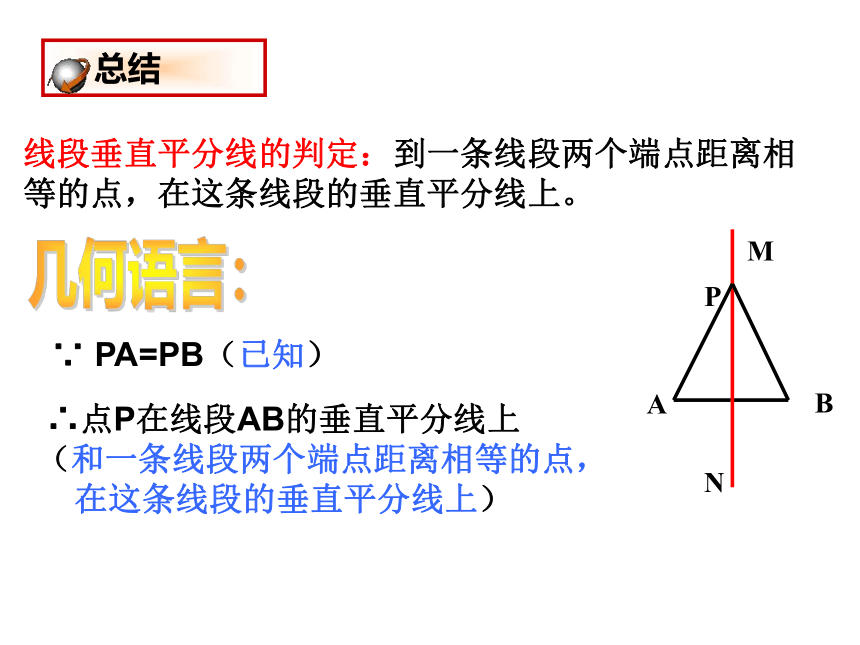
ABPMN线段垂直平分线的判定:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上。几何语言: 总结 运用1作图1.如图,A,B表示两个仓库,要在A,B一侧的河岸L边建造一个码头,使它到两个仓库的距离相等,码头应建造在什么位置? A●B●如图所示,点P即为所求作的点,
在点P处建码头,到两个仓库的距离相等。 PL例题1. 已知:如图,AB=AC=8cm ,DE是AB边的垂直平
分线交AC于点E,BC=6cm,求△BEC的周长证明: ∵ DE是AB边的中垂线 (已知)∴AE=BE(线段垂直平分线上任意
一点到这条线段两个端点的距离相等)
∴AE+EC=BE+EC=8cm
(等式性质)∵AC=8cm(已知)∵ △BEC的周长=BE+EC+BC(已知)
又∵ BC=6cm(已知)∴ △BEC的周长=8+6
=14cm.
有没有什么体会和大家分享?有垂直平分线,就有等腰三角形的产生 运用2
练习1. 已知:如图, 在△ ABC中,AB=AC , DE是AB边的垂直平分线交AC于点E,
求: 多少度?及时反思?合理设参数,引入方程求角度。 运用3例题2. 已知:如图,ΔABC中,BA=BC,边AB,BC的垂直平
分线交于P.
求证: 直线BP是边AC的垂直平分线BACMNM’N’P证明:∵点P在线段AB的垂直平分线上
∴PA=PB及时反思? 运用4 ∵点P在线段BC的垂直平分线上
∴PB=PC ∴PA=PC
∴点P在线段AC的垂直平分线上 ∵BA=BC
∴点B在线段AC的垂直平分线上 ∴直线BP是线段AC的垂直平分线 练习2.已知:在△ABC中,AB=AC,AB的垂直平分线线与AC所在的直线相交所得的夹角为50° 求:∠B等于多少度? 运用550°50°作图2,七宝镇政府打算修建一个体育中心.在选址过程中,有人建议该体育中心所在位置到三个中学 (如图中P,Q,R表示)的距离相等. (1)根据上述建议,试在图(1)中画出体育中心G的位置;(2)如果这三个中学的位置如图(2)所示,∠RPQ是一个钝角,那么根据上述建议,体育中心G应在什么位置? 学会运用作图3,分别作出直角三角形、锐角三角形、钝角三角形三边的垂直平分线,说明交点分别在什么位置.锐角三角形三边的垂直平分线交点在三角形内;直角三角形三边的垂直平分线交点在斜边上; 钝角三角形三边的垂直平分线交点在三角形外。 开拓创新分别作出直角三角形、锐角三角形、钝角三角形三边的垂直平分线,说明交点分别在什么位置.锐角三角形三边的垂直平分线交点在三角形内;直角三角形三边的垂直平分线交点在斜边上; 钝角三角形三边的垂直平分线交点在三角形外。 开拓创新
这节课你学到了什么?定理:线段垂直平分线上的点和这条线段两个端点的
距离相等。逆定理:和一条线段两个端点距离相等的点,
在这条线段的垂直平分线上。有垂直平分线,就有等腰三角形的产生三角形的三条边的垂直平分线相交于一点 总结驶向胜利的彼岸
点的距离相等吗?(1)等腰 ABC(其CA=CB)是轴对称图形,其对称轴是? 猜想ABCDPE猜测1:线段垂直平分线上的任意一点到这条线段两个
端点的距离相等。已知:直线MN⊥线段AB,垂足为点C, 且AC=CB.点P在MN上。
求证:PA=PBPC 验证证明:(1)当点P在点C处时,PA=PB成立。∵ MN⊥AB 于点C (已知)∴ ∠PCA= ∠PCB=90°(垂直的定义) 在 △PAC和△PBC中
AC=BC(已知)
∠PCA= ∠PCB(已证)
PC=PC(公共边)
∴ △PAC ≌△ PBC(SAS)∴PA=PB(全等三角形的对应边相等) (2)当点P不在C处时,线段垂直平分线的性质:线段垂直平分线上的任意一点 到这条线段两个端点的距离相等。几何语言:∵点P在线段AB的垂直平分线上(已知)∴PA=PB
(线段垂直平分线上的任意一点到这条线段两个端点的距离相等。 )
总结定理:线段垂直平分线上的任意一点到这条线段
两个端点的距离相等。PA=PB点P在线段AB的垂直平分线上条件和结论互换呢?思考:证明线段相等的方法有哪些?线段垂直平分线的性质 猜想猜测2:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上。已知:PA=PB求证:点P在AB的垂直平分线上证明: (1)当点P在线段AB上时,∵PA=PB(已知)∴AC=BC
(等腰三角形的“三线合一”)ABPC∴ MN是AB的垂直平分线∴P在AB的垂直平分线上
验证P在AB的垂直平分线上(2)当点P不在AB上时,过P点作MN⊥AB,垂足为C∵ PA=PB(已知) ∴点P在线段AB的垂直平分线上
(和一条线段两个端点距离相等的点,
在这条线段的垂直平分线上)
ABPMN线段垂直平分线的判定:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上。几何语言: 总结 运用1作图1.如图,A,B表示两个仓库,要在A,B一侧的河岸L边建造一个码头,使它到两个仓库的距离相等,码头应建造在什么位置? A●B●如图所示,点P即为所求作的点,
在点P处建码头,到两个仓库的距离相等。 PL例题1. 已知:如图,AB=AC=8cm ,DE是AB边的垂直平
分线交AC于点E,BC=6cm,求△BEC的周长证明: ∵ DE是AB边的中垂线 (已知)∴AE=BE(线段垂直平分线上任意
一点到这条线段两个端点的距离相等)
∴AE+EC=BE+EC=8cm
(等式性质)∵AC=8cm(已知)∵ △BEC的周长=BE+EC+BC(已知)
又∵ BC=6cm(已知)∴ △BEC的周长=8+6
=14cm.
有没有什么体会和大家分享?有垂直平分线,就有等腰三角形的产生 运用2
练习1. 已知:如图, 在△ ABC中,AB=AC , DE是AB边的垂直平分线交AC于点E,
求: 多少度?及时反思?合理设参数,引入方程求角度。 运用3例题2. 已知:如图,ΔABC中,BA=BC,边AB,BC的垂直平
分线交于P.
求证: 直线BP是边AC的垂直平分线BACMNM’N’P证明:∵点P在线段AB的垂直平分线上
∴PA=PB及时反思? 运用4 ∵点P在线段BC的垂直平分线上
∴PB=PC ∴PA=PC
∴点P在线段AC的垂直平分线上 ∵BA=BC
∴点B在线段AC的垂直平分线上 ∴直线BP是线段AC的垂直平分线 练习2.已知:在△ABC中,AB=AC,AB的垂直平分线线与AC所在的直线相交所得的夹角为50° 求:∠B等于多少度? 运用550°50°作图2,七宝镇政府打算修建一个体育中心.在选址过程中,有人建议该体育中心所在位置到三个中学 (如图中P,Q,R表示)的距离相等. (1)根据上述建议,试在图(1)中画出体育中心G的位置;(2)如果这三个中学的位置如图(2)所示,∠RPQ是一个钝角,那么根据上述建议,体育中心G应在什么位置? 学会运用作图3,分别作出直角三角形、锐角三角形、钝角三角形三边的垂直平分线,说明交点分别在什么位置.锐角三角形三边的垂直平分线交点在三角形内;直角三角形三边的垂直平分线交点在斜边上; 钝角三角形三边的垂直平分线交点在三角形外。 开拓创新分别作出直角三角形、锐角三角形、钝角三角形三边的垂直平分线,说明交点分别在什么位置.锐角三角形三边的垂直平分线交点在三角形内;直角三角形三边的垂直平分线交点在斜边上; 钝角三角形三边的垂直平分线交点在三角形外。 开拓创新
这节课你学到了什么?定理:线段垂直平分线上的点和这条线段两个端点的
距离相等。逆定理:和一条线段两个端点距离相等的点,
在这条线段的垂直平分线上。有垂直平分线,就有等腰三角形的产生三角形的三条边的垂直平分线相交于一点 总结驶向胜利的彼岸
