沪教版(五四学制)八年级上册第十九章几何证明:19.4 线段的垂直平分线 课件(17张PPT)
文档属性
| 名称 | 沪教版(五四学制)八年级上册第十九章几何证明:19.4 线段的垂直平分线 课件(17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 252.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-10 00:00:00 | ||
图片预览






文档简介
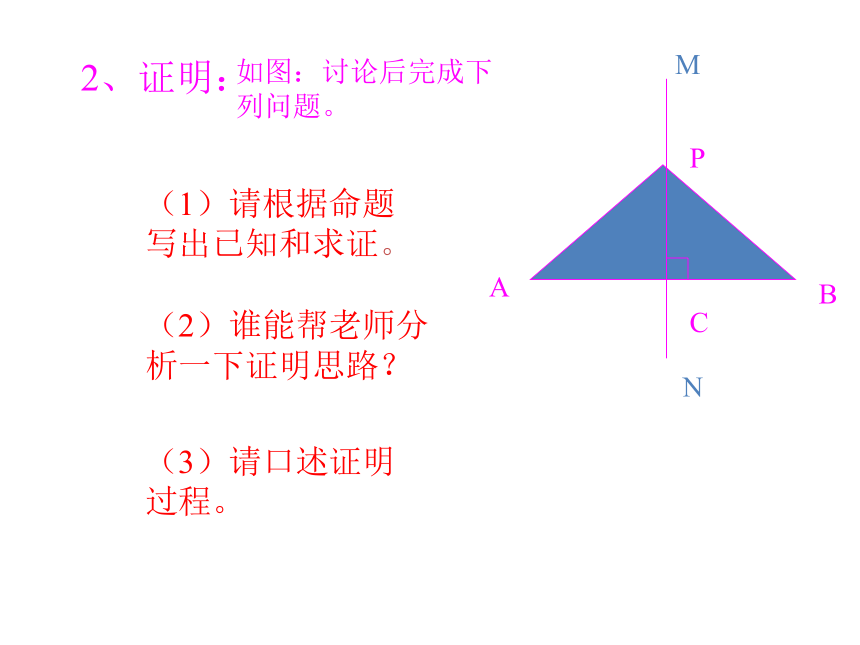
课件17张PPT。线段的垂直平分线性质PA=PBP1P1A=P1B……命题:线段垂直平分线上的点和这条线段两个端点的距离相等。由此你能得到什么规律?2、证明:MNABPC如图:讨论后完成下列问题。(1)请根据命题写出已知和求证。(2)谁能帮老师分析一下证明思路?(3)请口述证明过程。命题:线段垂直平分线上的点和这条线段两个端点的距离相等。当点P与点C重合时,上述证明有什么缺陷?CCPA=PB点P在线段AB的垂直平分线上性质定理有何作用?可证明线段相等定理应用格式:
∵AC=BC,MN⊥AB,P是MN上任意一点(已知),
∴PA=PB(线段垂直平分线上的点与这条线段两个端点距离相等).线段垂直平分线性质 如图,在△ABC中,BC=8cm,AB的垂直平分线交AB于点D,交边AC于点E,△BCE的周长等于18cm,则AC的长等于( ).
A.6cm B.8cm C.10cm D.12cm例1 2、在△ABC,PM,QN分别垂直平分AB,AC,若BC=10cm则△APQ的周长=_____若∠BAC=100°则∠PAQ=_________ 10cm200例2 已知:如图,在ΔABC中,边AB,BC的垂直平分线交于P.
求证:PA=PB=PC;变式题:如图所示,直线MN和DE分别是线段AB、BC的垂直平分线,它们交于点O,试判断线段OA和OC是否相等?请说明理由?解:相等,连接OB.∵ MN是线段AB的垂直平分线(已知)∴ OA=OB(线段中垂线的性质)
又∵ DE是线段BC的垂直平分线
(已知)∴ OB=OC(线段中垂线的性质)∴ OA=OC(等量代换)注意辅助线的做法 张店区政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处,才能使得它到三个小区的距离相等。ABC实际问题求作一点P,使它和已△ABC的三个顶点距离相等.实际问题CPA=PB点P在线段AB的垂直平分线上2.性质定理有何用?可证明线段相等课堂小结3线段垂直平分线性质的应用及辅助线的运用线段垂直平分线性质定理
线段垂直平分线上的点和这条线段
两个端点的距离相等.和线段垂直平分线性质的应用及辅助线的运用
在这条线段的垂直平分线上..
小结:作业:
P131 2. 3. 4思考题1如图,房屋开发商准备建一个三角形住宅小区,A、B两幢建筑物恰好建在三角形住宅小区的两个顶点处,现要求小区大门C建在河边且小区周边最短。如果你是这个项目的总设计师,请确定出小区大门C的最佳位置。并在图中标出。mAB提示1.小区的周边,哪一条边的长度是固定不变的?2.要使小区周边最短,只需哪两边的和最短?2在△ABC中,D为BC 的点,DE⊥BC交∠BAC的平分线AE于点,EF⊥AB于F点,EG⊥AC于G点
求证:BF=CG
∵AC=BC,MN⊥AB,P是MN上任意一点(已知),
∴PA=PB(线段垂直平分线上的点与这条线段两个端点距离相等).线段垂直平分线性质 如图,在△ABC中,BC=8cm,AB的垂直平分线交AB于点D,交边AC于点E,△BCE的周长等于18cm,则AC的长等于( ).
A.6cm B.8cm C.10cm D.12cm例1 2、在△ABC,PM,QN分别垂直平分AB,AC,若BC=10cm则△APQ的周长=_____若∠BAC=100°则∠PAQ=_________ 10cm200例2 已知:如图,在ΔABC中,边AB,BC的垂直平分线交于P.
求证:PA=PB=PC;变式题:如图所示,直线MN和DE分别是线段AB、BC的垂直平分线,它们交于点O,试判断线段OA和OC是否相等?请说明理由?解:相等,连接OB.∵ MN是线段AB的垂直平分线(已知)∴ OA=OB(线段中垂线的性质)
又∵ DE是线段BC的垂直平分线
(已知)∴ OB=OC(线段中垂线的性质)∴ OA=OC(等量代换)注意辅助线的做法 张店区政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处,才能使得它到三个小区的距离相等。ABC实际问题求作一点P,使它和已△ABC的三个顶点距离相等.实际问题CPA=PB点P在线段AB的垂直平分线上2.性质定理有何用?可证明线段相等课堂小结3线段垂直平分线性质的应用及辅助线的运用线段垂直平分线性质定理
线段垂直平分线上的点和这条线段
两个端点的距离相等.和线段垂直平分线性质的应用及辅助线的运用
在这条线段的垂直平分线上..
小结:作业:
P131 2. 3. 4思考题1如图,房屋开发商准备建一个三角形住宅小区,A、B两幢建筑物恰好建在三角形住宅小区的两个顶点处,现要求小区大门C建在河边且小区周边最短。如果你是这个项目的总设计师,请确定出小区大门C的最佳位置。并在图中标出。mAB提示1.小区的周边,哪一条边的长度是固定不变的?2.要使小区周边最短,只需哪两边的和最短?2在△ABC中,D为BC 的点,DE⊥BC交∠BAC的平分线AE于点,EF⊥AB于F点,EG⊥AC于G点
求证:BF=CG
