六年级下册数学课件《综合与实践》冀教版 (共19张PPT)
文档属性
| 名称 | 六年级下册数学课件《综合与实践》冀教版 (共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-08 11:07:01 | ||
图片预览



文档简介
(共19张PPT)
人教版小学数学六年级下册
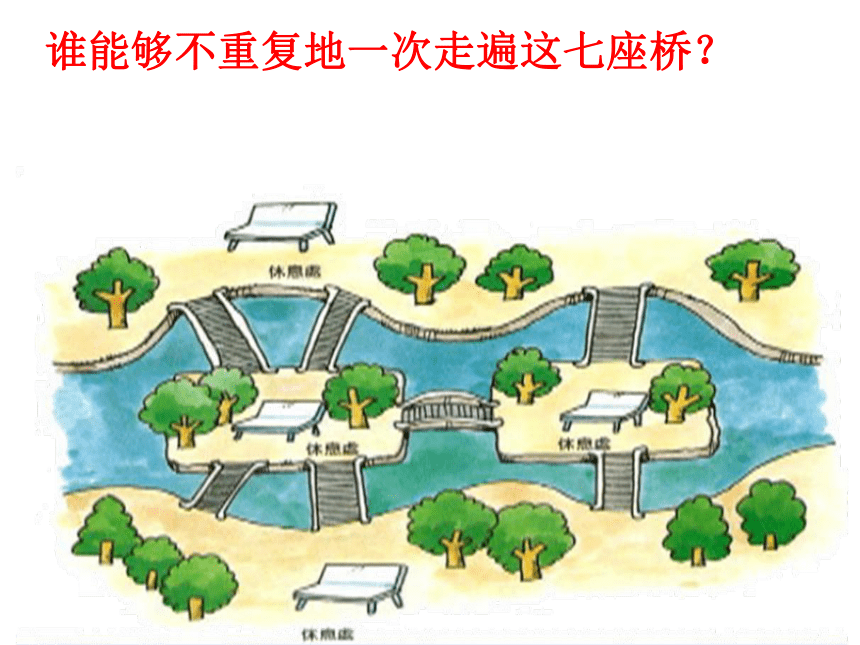
谁能够不重复地一次走遍这七座桥?
人教版小学数学六年级下册
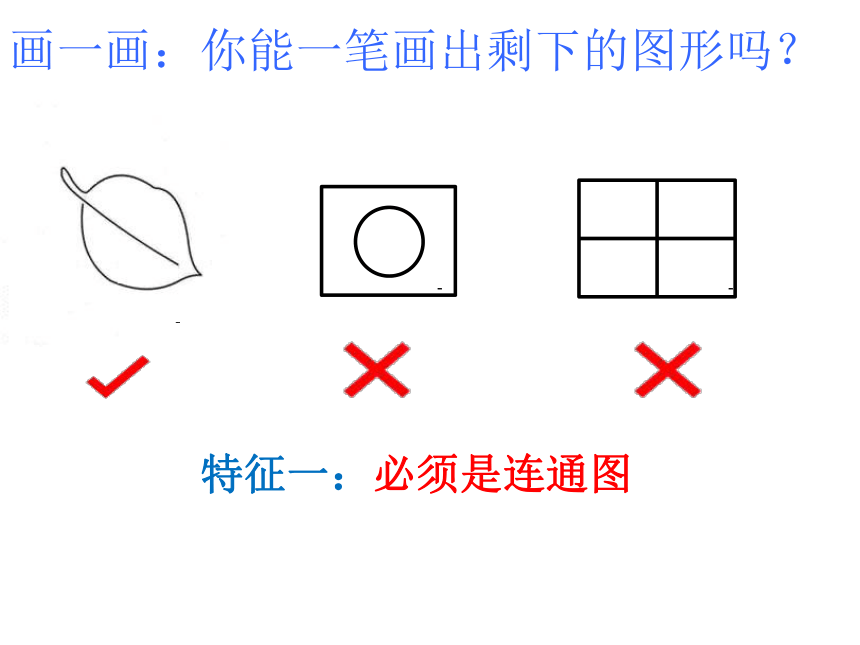
画一画:你能一笔画出剩下的图形吗?
特征一:必须是连通图
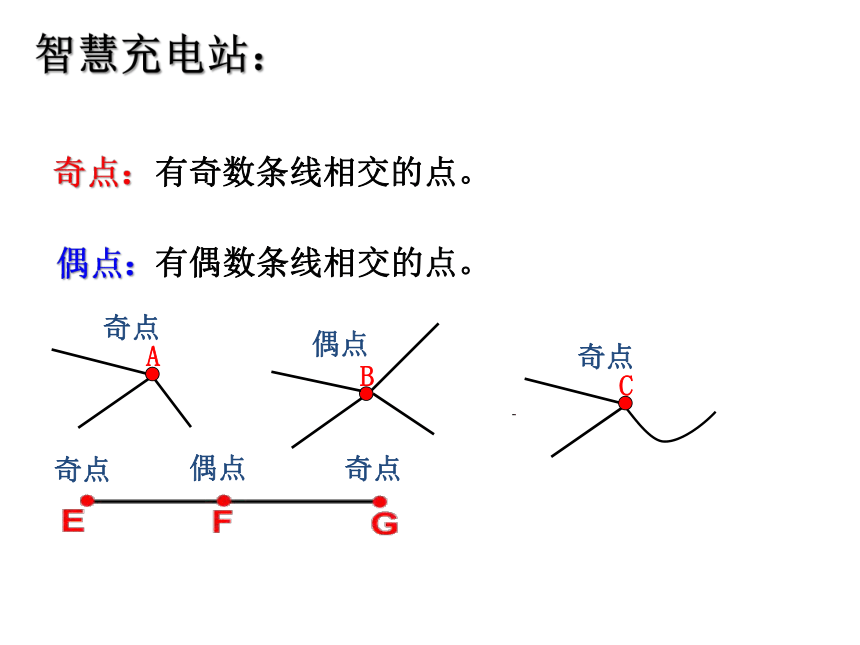
智慧充电站:
有奇数条线相交的点。
有偶数条线相交的点。
奇点
偶点
奇点
C
B
A
奇点:
偶点:
奇点
奇点
偶点
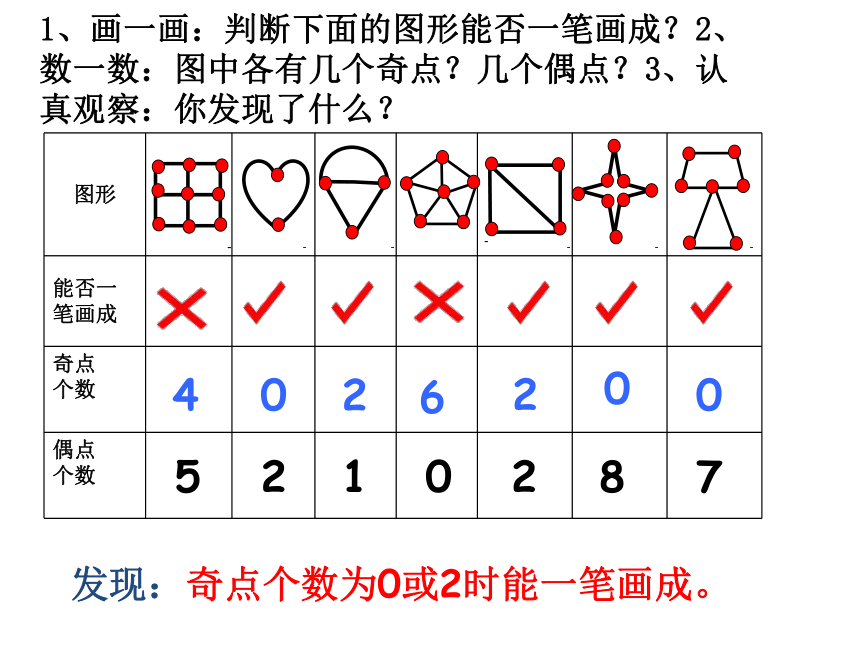
图形
能否一笔画成
奇点
个数
偶点
个数
4
0
2
6
2
0
0
5
2
1
0
2
8
7
发现:奇点个数为0或2时能一笔画成。
1、画一画:判断下面的图形能否一笔画成?2、数一数:图中各有几个奇点?几个偶点?3、认真观察:你发现了什么?
小组实验要求
1、画一画:每人画一个一笔画图形(组合图形、绘画、文字、字母等),并标出各点,要求一笔画有创意。
2、数一数:所画图形中奇点和偶点的个数。
3、议一议:得出什么结论?
特征二:奇点个数为0或2时,一定能一笔画成,与偶点个数无关。
从任意一点出发,都可以一笔画出来。
只能以一个奇点为起点,另一个奇点为终点,才能一笔画出来。
特征三:
0个奇点的图形:
2个奇点的图形:
超市
医院
广场
学校
公园
一辆洒水车给城市街道洒水,从哪里出发,才能让
洒水车一次不重复的走遍所有街道?请你说出它的
洒水路线?
奇点
奇点
欧 拉
(公元1707-1783)
课后思考:如果允许再架一座桥,能否不重复地一次走遍这八座桥?这座桥应架在哪里?
A
B
D
C
不可能
A
B
C
D
没有大胆的猜想,就没有伟大的
发明和发现。
——牛顿
奇点
奇点
奇点
偶点
偶点
奇点
练一练:你能说说下图中哪些点是奇点,哪些点是偶点吗?
A
B
C
D
E
F
`
G
偶点
画一画:
1、你能一笔画出以下图形吗?
必须是连通图
2、对于能够一笔画出的图形,请沿不同交
点出发,探索它有几种不同的画法。
4个奇点
2个奇点
A
B
C
D
A
B
C
D
E
练一练:下面的图形哪些能一笔画成?
哪些不能?
哥尼斯堡七桥问题
这个问题困扰了当地居民很长时间,大家纷纷来到小岛上试图找到答案,但都无功而返。因为根据计算,每次都走完七座桥的所有走法共有5040种,这么多怎么走得完呢 后来有人写信向当时公认的“天才数学家”欧拉请教。欧拉亲自来到小岛上实地考察,也未找到答案。但他是一个不向困难低头的人,经过一断时间的研究,终于解决了这个问题。
知识链接
活动探究二:一笔画的画法
B
A
C
2个奇点
0个奇点的图形,从任意一点出发,都可以一笔画出来。
2个奇点的图形,只能以一个奇点为起点,另一个奇点为终点,才能一笔画出来。
B
0个奇点
A
C
写出以下一笔画的路径,用字母和箭头表示,并找出起点和终点,你有什么发现?
A
B
C
A
A
B
C
A
B
A
B
C
A
B
智慧充电站:
B
有奇数条线相交的点,我们称之为奇点。
有偶数条线相交的点,我们称之为偶点。
A
C
奇点
偶点
奇点
A
B
C
E
F
G
H
M
N
P
D
奇点
奇点
公园这么多景点,出口和入口设在哪儿才能让
游客不重复地一次游览完所有的景点?
公园平面图
人教版小学数学六年级下册
谁能够不重复地一次走遍这七座桥?
人教版小学数学六年级下册
画一画:你能一笔画出剩下的图形吗?
特征一:必须是连通图
智慧充电站:
有奇数条线相交的点。
有偶数条线相交的点。
奇点
偶点
奇点
C
B
A
奇点:
偶点:
奇点
奇点
偶点
图形
能否一笔画成
奇点
个数
偶点
个数
4
0
2
6
2
0
0
5
2
1
0
2
8
7
发现:奇点个数为0或2时能一笔画成。
1、画一画:判断下面的图形能否一笔画成?2、数一数:图中各有几个奇点?几个偶点?3、认真观察:你发现了什么?
小组实验要求
1、画一画:每人画一个一笔画图形(组合图形、绘画、文字、字母等),并标出各点,要求一笔画有创意。
2、数一数:所画图形中奇点和偶点的个数。
3、议一议:得出什么结论?
特征二:奇点个数为0或2时,一定能一笔画成,与偶点个数无关。
从任意一点出发,都可以一笔画出来。
只能以一个奇点为起点,另一个奇点为终点,才能一笔画出来。
特征三:
0个奇点的图形:
2个奇点的图形:
超市
医院
广场
学校
公园
一辆洒水车给城市街道洒水,从哪里出发,才能让
洒水车一次不重复的走遍所有街道?请你说出它的
洒水路线?
奇点
奇点
欧 拉
(公元1707-1783)
课后思考:如果允许再架一座桥,能否不重复地一次走遍这八座桥?这座桥应架在哪里?
A
B
D
C
不可能
A
B
C
D
没有大胆的猜想,就没有伟大的
发明和发现。
——牛顿
奇点
奇点
奇点
偶点
偶点
奇点
练一练:你能说说下图中哪些点是奇点,哪些点是偶点吗?
A
B
C
D
E
F
`
G
偶点
画一画:
1、你能一笔画出以下图形吗?
必须是连通图
2、对于能够一笔画出的图形,请沿不同交
点出发,探索它有几种不同的画法。
4个奇点
2个奇点
A
B
C
D
A
B
C
D
E
练一练:下面的图形哪些能一笔画成?
哪些不能?
哥尼斯堡七桥问题
这个问题困扰了当地居民很长时间,大家纷纷来到小岛上试图找到答案,但都无功而返。因为根据计算,每次都走完七座桥的所有走法共有5040种,这么多怎么走得完呢 后来有人写信向当时公认的“天才数学家”欧拉请教。欧拉亲自来到小岛上实地考察,也未找到答案。但他是一个不向困难低头的人,经过一断时间的研究,终于解决了这个问题。
知识链接
活动探究二:一笔画的画法
B
A
C
2个奇点
0个奇点的图形,从任意一点出发,都可以一笔画出来。
2个奇点的图形,只能以一个奇点为起点,另一个奇点为终点,才能一笔画出来。
B
0个奇点
A
C
写出以下一笔画的路径,用字母和箭头表示,并找出起点和终点,你有什么发现?
A
B
C
A
A
B
C
A
B
A
B
C
A
B
智慧充电站:
B
有奇数条线相交的点,我们称之为奇点。
有偶数条线相交的点,我们称之为偶点。
A
C
奇点
偶点
奇点
A
B
C
E
F
G
H
M
N
P
D
奇点
奇点
公园这么多景点,出口和入口设在哪儿才能让
游客不重复地一次游览完所有的景点?
公园平面图
